
We now describe the fastest attack on our scheme of which we are
aware. An attacker who captures the device on which the key is
generated but who has no information about the user's distinguishing
features may attack the system by repeatedly guessing a feature
descriptor ![]() at random and solving (4). If there are
at random and solving (4). If there are
![]() distinguishing features then each guess will be successful with
probability
distinguishing features then each guess will be successful with
probability ![]() , but will require the attacker to solve a system
of
, but will require the attacker to solve a system
of ![]() linear equations, which is quite time consuming. A faster
approach is to choose feature descriptors
linear equations, which is quite time consuming. A faster
approach is to choose feature descriptors
![]() such that
each differs from the last in one bit. Then, computing
such that
each differs from the last in one bit. Then, computing
![]() requires only one new Gaussian elimination step per
requires only one new Gaussian elimination step per
![]() , and the further optimizations outlined in
Section 4.2 can also be applied in this case.
, and the further optimizations outlined in
Section 4.2 can also be applied in this case.
The expected time for this attack to succeed can be computed as
follows. Assume that ![]() and
and ![]() differ in exactly one
position that is chosen at random. Let
differ in exactly one
position that is chosen at random. Let ![]() for
for ![]() denote
the expected number of Gaussian elimination steps performed until
reaching a
denote
the expected number of Gaussian elimination steps performed until
reaching a ![]() with no errors (i.e., that is consistent with all of
the user's distinguishing features), assuming that
with no errors (i.e., that is consistent with all of
the user's distinguishing features), assuming that ![]() has
has ![]() errors. Note that
errors. Note that ![]() has a different number of errors than
has a different number of errors than ![]() with probability
with probability ![]() , and if it has a different number of errors,
then it decreases the number of errors (by one) with probability
, and if it has a different number of errors,
then it decreases the number of errors (by one) with probability ![]() and increases it with probability
and increases it with probability ![]() . Hence, we get the
following equations for
. Hence, we get the
following equations for ![]() .
.
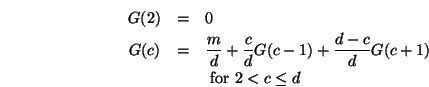
Solving for these linear equations at ![]() yields the expected
number of Gaussian elimination steps before recovering the key, since
a random feature descriptor contains an expected
yields the expected
number of Gaussian elimination steps before recovering the key, since
a random feature descriptor contains an expected ![]() errors.
Moreover, after the Gaussian elimination step for each
errors.
Moreover, after the Gaussian elimination step for each ![]() ,
, ![]() multiplications are required to test
multiplications are required to test ![]() on average. So, the total
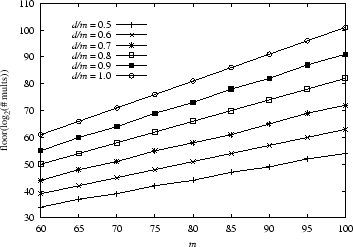
cost of this attack is as shown in Figure 3.
(Actually, this is a conservative lower bound, since the cost of each
Gaussian elimination step itself is not counted.)
on average. So, the total
cost of this attack is as shown in Figure 3.
(Actually, this is a conservative lower bound, since the cost of each
Gaussian elimination step itself is not counted.)
 |
In the empirical evaluation that we perform in
Section 5, we evaluate our approach at ![]() , which
is the smallest value of
, which
is the smallest value of ![]() shown in Figure 3.
Here, if
shown in Figure 3.
Here, if ![]() of the features are distinguishing, then this attack
conservatively requires an expected
of the features are distinguishing, then this attack
conservatively requires an expected ![]() multiplications. If
multiplications. If
![]() of the features are distinguishing, then this attack requires
at least
of the features are distinguishing, then this attack requires
at least ![]() multiplications on average. Obviously the security
of the scheme improves as
multiplications on average. Obviously the security
of the scheme improves as ![]() and
and ![]() are increased, and this is a
goal of our ongoing work.
are increased, and this is a
goal of our ongoing work.