
To test the performance of our key reconstruction routines we devised
the following experiment. First, an ![]() table of shares of
the key
table of shares of
the key ![]() is generated as outlined in Section 2,
i.e., as a user's key regeneration table would be initialized in
practice. Then,
is generated as outlined in Section 2,
i.e., as a user's key regeneration table would be initialized in
practice. Then, ![]() rows of the table (features) are selected at
random to be distinguishing, and one element of each of these
rows of the table (features) are selected at
random to be distinguishing, and one element of each of these ![]() rows
is perturbed randomly--as if the user were consistent in utilizing
the other element of this row (see Section 2).
Finally, a feature descriptor
rows
is perturbed randomly--as if the user were consistent in utilizing
the other element of this row (see Section 2).
Finally, a feature descriptor ![]() is chosen with the property that
is chosen with the property that
![]() of the
of the ![]() distinguishing features (chosen at
random), say
distinguishing features (chosen at
random), say
![]() , are ``errors'', i.e., are set to
select the randomly perturbed elements of rows
, are ``errors'', i.e., are set to
select the randomly perturbed elements of rows
![]() .
The key reconstruction process performs a number of reconstructions
that depends on
.
The key reconstruction process performs a number of reconstructions
that depends on ![]() in its attempts to correct for such errors; the
number of reconstructions performed in the worst case is shown in
expression (2) of Section 2.
Our benchmark is the amount of time required to reconstruct the key
in its attempts to correct for such errors; the
number of reconstructions performed in the worst case is shown in
expression (2) of Section 2.
Our benchmark is the amount of time required to reconstruct the key
![]() on average, which is a rough measure of the time required to
perform
on average, which is a rough measure of the time required to
perform
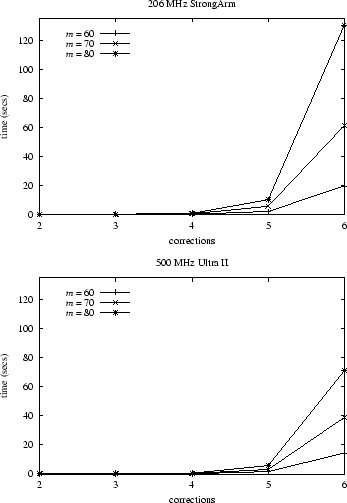 |
Our results for this benchmark, shown in Figure 2, are significantly less than multiplying (5) by the time to perform and test a single reconstruction in our secret sharing scheme. The reason is due to the significant optimizations that can be achieved as described in Section 4.2.