


Next: Performance
Up: Encoding Scheme
Previous: Initialization
Key reconstruction
As described in Section 2, the input from the user,
in this case an utterance, is used to generate an 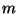 -bit feature
descriptor
-bit feature
descriptor 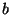 . The key regeneration program constructs a vector
. The key regeneration program constructs a vector
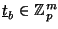 by selecting the corresponding elements of the
table, i.e.,
by selecting the corresponding elements of the
table, i.e.,
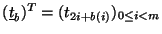 . It
similarly constructs a
. It
similarly constructs a
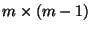 matrix
matrix
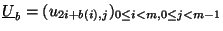 . Note that solving
. Note that solving
 |
(4) |
for
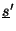 would yield
would yield
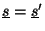 if
if 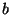 contained no user
errors, and the fact that
contained no user
errors, and the fact that
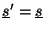 could be confirmed by
testing whether
could be confirmed by
testing whether
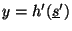 . However, since instantiating and
solving (4) for all the different feature descriptors
. However, since instantiating and
solving (4) for all the different feature descriptors
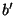 within Hamming distance
within Hamming distance 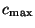 from
from 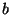 would require too
much time on the target device, our error correction strategy takes a
different approach.
This faster approach derives from the observation that the equation
would require too
much time on the target device, our error correction strategy takes a
different approach.
This faster approach derives from the observation that the equation
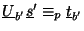 for a feature descriptor
for a feature descriptor 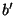 contains
contains 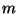 equations in
equations in 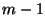 unknowns, and thus is over-defined.
This is intentional, and allows
unknowns, and thus is over-defined.
This is intentional, and allows 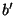 to be rejected very quickly if
this equation has no solution. Specifically, let
to be rejected very quickly if
this equation has no solution. Specifically, let
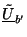 be the
be the 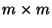 matrix whose first
matrix whose first 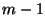 columns are the same as
columns are the same as
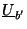 and whose last column is
and whose last column is
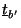 . Then, a solution
exists only if
. Then, a solution
exists only if
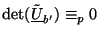 , and so if
, and so if
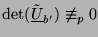 then
then 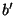 can be discarded
from further consideration. Using a recursive algorithm, it is
possible to check
can be discarded
from further consideration. Using a recursive algorithm, it is
possible to check
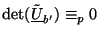 for feature
descriptors
for feature
descriptors 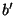 within
within 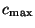 errors of
errors of 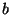 using only one
additional Gaussian elimination step per new
using only one
additional Gaussian elimination step per new 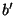 . Due to this
feature, our implementation can test over
. Due to this
feature, our implementation can test over 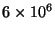 feature
descriptors
feature
descriptors 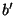 per second when
per second when 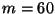 .
.
Two further observations are worth noting here. First, the
determinant of even a randomly chosen matrix is 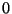 mod
mod 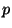 with
probability
with
probability 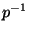 , which is not negligible since
, which is not negligible since 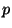 is chosen to
be small. Therefore, if
is chosen to
be small. Therefore, if
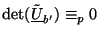 and so
we proceed to solve
and so
we proceed to solve
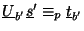 for
for
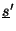 , it remains necessary to confirm
, it remains necessary to confirm
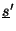 by checking
by checking
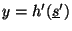 . Second, there is a small chance that (4)
is not solvable even if
. Second, there is a small chance that (4)
is not solvable even if 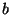 is consistent with all the user's
distinguishing features, because
is consistent with all the user's
distinguishing features, because
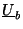 might not have full rank.
Under the assumption that
might not have full rank.
Under the assumption that
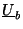 is chosen uniformly at random, it
follows that
is chosen uniformly at random, it
follows that
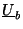 has rank
has rank 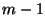 with probability
with probability
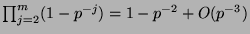 . This probability is
much smaller than the probability that the system cannot be solved
because the feature descriptor
. This probability is
much smaller than the probability that the system cannot be solved
because the feature descriptor 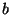 induced by the user's utterance
contains more than
induced by the user's utterance
contains more than 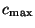 errors, and thus can be ignored.
errors, and thus can be ignored.


Next: Performance
Up: Encoding Scheme
Previous: Initialization
fabian
2002-08-28

![]() mod
mod ![]() with
probability
with
probability ![]() , which is not negligible since
, which is not negligible since ![]() is chosen to
be small. Therefore, if
is chosen to
be small. Therefore, if
![]() and so
we proceed to solve
and so
we proceed to solve
![]() for
for
![]() , it remains necessary to confirm
, it remains necessary to confirm
![]() by checking
by checking
![]() . Second, there is a small chance that (4)
is not solvable even if
. Second, there is a small chance that (4)
is not solvable even if ![]() is consistent with all the user's
distinguishing features, because
is consistent with all the user's
distinguishing features, because
![]() might not have full rank.
Under the assumption that
might not have full rank.
Under the assumption that
![]() is chosen uniformly at random, it
follows that
is chosen uniformly at random, it
follows that
![]() has rank
has rank ![]() with probability
with probability
![]() . This probability is
much smaller than the probability that the system cannot be solved
because the feature descriptor
. This probability is
much smaller than the probability that the system cannot be solved
because the feature descriptor ![]() induced by the user's utterance
contains more than
induced by the user's utterance
contains more than ![]() errors, and thus can be ignored.
errors, and thus can be ignored.