


Next: Merging Groups
Up: Role Classification
Previous: Role Classification
Forming Groups
Group formation can be thought of as a graph theory problem. From the
connection sets of I, one can generate a neighborhood graph,
nbh-graph, where each node represents a host and each edge with
weight e represents that there are e common neighbors between the
hosts. Thus, a neighborhood graph captures the extent to which pairs of
hosts communicate with the same set of other hosts. We use an undirected
graph since almost all communication between hosts in the intranets is
bi-directional. However, in certain situations, directionality may be
used to improve the quality of the grouping results and we continue to
investigate this issue.
One approach to the grouping problem is to treat it as a k-clique
problem where nbh-graph is partitioned into cliques of size k in
which each edge in the clique has a weight greater than or equal to some
constant c. Once a k-clique is identified, one assigns all the
nodes in the k-clique to one group, since they all share at least c
common neighbors. This approach is problematic, because (i) the
k-clique problem is NP-complete [25], and (ii) requiring
that each host pair in a group has exactly k common neighbors is too
strong a requirement.
Another approach is to treat grouping as related to the problem of
identifying bi-connected components (BCCs). A BCC is a connected
component in which any two edges lie in a simple cycle. Thus, there
exist at least two disjoint paths between any two nodes in a BCC.
Unlike the k-clique problem, BCC can be solved in O(N+E), where N
and E are the number of nodes and edges in the graph
respectively [9,27]. Moreover, all nodes in the BCC
need not be connected to each other directly. This approach is the one we
use.
The group formation phase operates as follows:
- 1.
- Generate the connectivity graph, conn-graph, based on the
observed connection patterns.
- 2.
- For k=kmax down to 1, where kmax is the maximum number
of hosts with which a single host communicates:
- Repeat until no new groups can be assigned:
- From conn-graph, build the k-neighborhood graph
k-nbh-graph.
- Remove group nodes (see 2d) from k-nbh-graph.
- Generate all BCCs in k-nbh-graph.
- For each BCC B, replace in conn-graph the nodes
in B by a new group node G representing those nodes. Label G by a
pair (IDG, KG), where IDG is a unique identifier and
KG is k. (KG will be used later to compute the degree of
similarity between groups.)
- For each ungrouped host h, where
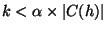 and
and
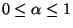 , create a new group G containing only h
as described in 2d.
, create a new group G containing only h
as described in 2d.
The algorithm runs iteratively over conn-graph until no
ungrouped node remains or k = 0. At each step multiple BCCs may be
identified simultaneously and a single node could be a part of several
BCCs indicating that it may share multiple roles. In this case, the
node becomes a part of a BCC with the largest size. If more than one
such BCC exists, we choose one randomly. By iterating over k from
high to low, the algorithm associates each host h with other hosts
with the strongest similarity.
In the grouping algorithm, the minimum number of nodes required to
form a BCC is two. Technically, the minimum number of nodes to form a
BCC is 3, since we do not allow duplicate edges between any two
nodes. Nevertheless, we allow two isolated nodes connected by an edge
to form a group.
Since a BCC is not a clique, some node pairs in the BCC may not have
edges between them allowing node pairs that do not share at least k
common neighbors to be in the same group. However, any two nodes in a
BCC have at least two disjoint paths along which two successive nodes
share at least k common neighbors. In other words, any two nodes in a
group demonstrate in at least two different ways that they have strong
similarity in connection habits, significantly reducing the possibility
that they may serve different roles. This observation is a major reason
why we believe BCCs are suitable for forming groups.
When a set of hosts is placed into a group, the nodes representing those
hosts are removed from conn-graph and replaced by one node (called
the group node) representing the entire group. There are edges
connecting that group node to each node to which one of the hosts in the
group was connected.
In some cases where a node may have connection patterns so different
from any other nodes, the node should form a group by itself.
Step 2e forms a new group with only h in it if there
exist no nodes that have the number of common neighbors greater than or
equal to
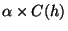 . We set
. We set 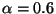 and find that it
works well with various networks.
and find that it
works well with various networks.
Figure 2:
Evolution of the grouping algorithm at various k values.
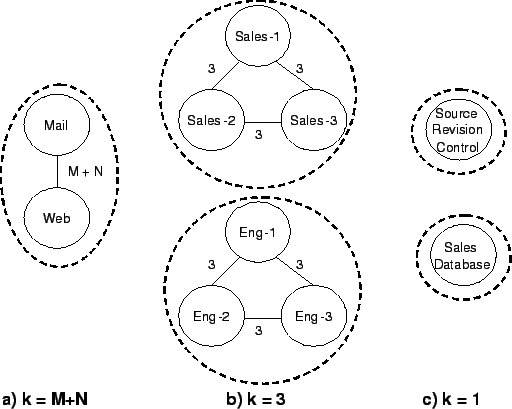 |
Figure 2 illustrates the evolution of the grouping
algorithm, in terms of k-nbh-graph, for the network depicted in
Figure 1. The first group is formed when k = M + N,
where M is the number of hosts used by sales personnels and N is the
number of hosts used by engineers. For specificity, let us assume that
M = N = 3. As shown in the picture, the 6-nbh-graph contains
two hosts, Mail and Web, and the algorithm puts them in one
group. When k = 3, the algorithm identifies two additional BCCs, one
containing all the sales machines and the other, all the engineering
machines. Finally, because of the bootstrap condition (see
Step 2e), the algorithm creates two groups, one
containing SalesDatabase and the other,
SourceRevisionControl, when
k = 1 < 0.6 x M.


Next: Merging Groups
Up: Role Classification
Previous: Role Classification
Godfrey Tan
2003-04-01
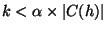 and
and
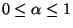 , create a new group G containing only h
as described in 2d.
, create a new group G containing only h
as described in 2d.

