 |

![[*]](cross_ref_motif.png) end figure
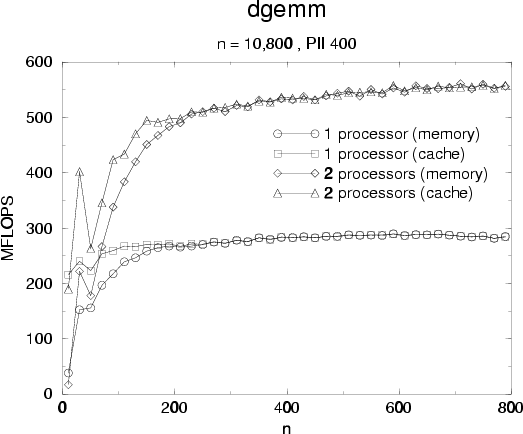
end figure ![[*]](cross_ref_motif.png) performances and acceleration are very good and remain as the size of matrices
increase.
Performances for dgemm are important because it's a building block for block LU
factorization. We know outline a block LU factorization method, the reader may refer
to [5] for an in-deep analysis and algorithms, and discuss how
multi-threaded version can be realized.
performances and acceleration are very good and remain as the size of matrices
increase.
Performances for dgemm are important because it's a building block for block LU
factorization. We know outline a block LU factorization method, the reader may refer
to [5] for an in-deep analysis and algorithms, and discuss how
multi-threaded version can be realized.
LU factorization is used to solve linear system like A.X=B by factorize
A into L.U where L is a lower triangular unit matrix and U is an upper
triangular matrix. Efficient LU methods rely on matrix matrix product and we
outline such method in the following.
For simplicity we suppose that the block size nb divide n which is the
size of the square matrix A and set N = n/nb. Each block of A is
numbered
![]() .
The block LU performs as follow:
.
The block LU performs as follow:
Step 2 uses subroutine dgetf2 from LAPACK, row interchange is done
using dlaswp, step 3 and 4 use dtrsm (triangular solve with multiple right hand
side) and step 5 uses dgemm. It is important to note that most computation is
done in steps 4 and 5 which use level 3 BLAS and represent 1-1/N2 of the
floating point operations issued (see[5]). Figure
![[*]](cross_ref_motif.png) presents task dependencies in block LU for step k, it outlines a
graph dependency for a parallel implementation. At this point we have two
choices for multi-threaded version:
presents task dependencies in block LU for step k, it outlines a
graph dependency for a parallel implementation. At this point we have two
choices for multi-threaded version:
The first solution requires to construct the dependency graph and more complex synchronization scheme but always based on synchronization variable. Construct the graph and searching for ready task may be a serious overhead thus limiting acceleration. The second solution let the LU task be a sequential bottleneck and use parallelism only on level 3 operations.
For implementation we choose the second solution because it's simple and LU
bottleneck is in fact very small since it represents only 1/N2 of the
overall job. Results for our block LU factorization are presented
figure ![[*]](cross_ref_motif.png) and figure
and figure ![[*]](cross_ref_motif.png) : we use dgetrf from
ATLAS as a reference code for our sequential block LU. Acceleration figure
presents two curves; one presents acceleration obtained by the multi-threaded
block LU, the other (ideal acceleration) is computed using the sequential code
by looking for time spent in dgetf2 and in level 3 operation:
: we use dgetrf from
ATLAS as a reference code for our sequential block LU. Acceleration figure
presents two curves; one presents acceleration obtained by the multi-threaded
block LU, the other (ideal acceleration) is computed using the sequential code
by looking for time spent in dgetf2 and in level 3 operation: