


Next: 3.5 Reliable FastReplica Algorithm
Up: 3 FastReplica Algorithm
Previous: 3.3 Preliminary Performance Analysis
3.4 FastReplica in the Large
In this Section, we generalize FastReplica in the small to a
case where a set of nodes to which a file has to be replicated can be
in the range of hundreds/thousands of nodes.
Let 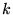 be a number of network connections chosen for concurrent
transfers between a single node and multiple receiving nodes (i.e.
be a number of network connections chosen for concurrent
transfers between a single node and multiple receiving nodes (i.e. 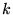 limits the number of nodes in the group for Multiple Unicast or
FastReplica strategies). An appropriate value of
limits the number of nodes in the group for Multiple Unicast or
FastReplica strategies). An appropriate value of 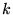 can be
experimentally determined via probing. Heterogeneous nodes might be
capable of supporting a different number of connections. Let
can be
experimentally determined via probing. Heterogeneous nodes might be
capable of supporting a different number of connections. Let 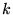 be
the number of connections suitable for most of the nodes in the
overall replication set.
A natural way to scale FastReplica in the small to a large
number of nodes is:
be
the number of connections suitable for most of the nodes in the
overall replication set.
A natural way to scale FastReplica in the small to a large
number of nodes is:
- partition the original set of nodes into
replication groups, each consisting of
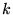 nodes;
nodes;
- apply FastReplica in the small iteratively: first,
replicate the original file
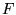 to a group of
to a group of 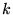 nodes, and then use
these
nodes, and then use
these 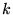 nodes as the origin nodes with file
nodes as the origin nodes with file 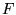 to repeat the same
procedure to a new groups of nodes, etc.
to repeat the same
procedure to a new groups of nodes, etc.
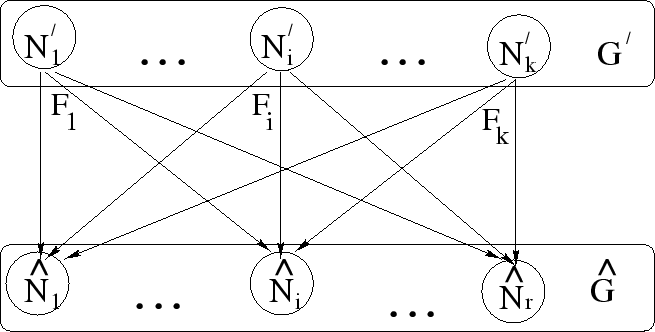
Schematically, this procedure is shown in
Figure 6, where circles represent the nodes, and
boxes represent the replication groups. The arrows, connecting one
node with a set of other nodes, reflect the origin node and the
recipient nodes, involved in communications on a particular iteration
of the algorithm.
Figure 6:
FastReplica in the large: iterative replication
process.
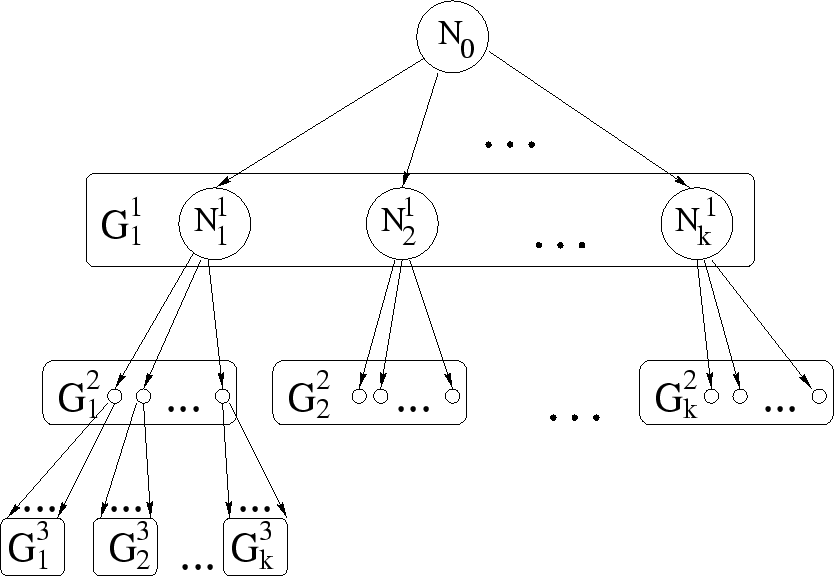 |
At the first iteration, node 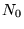 replicates file
replicates file 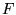 to group
to group
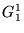 , consisting of
, consisting of 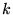 nodes, by using the FastReplica in the
small algorithm.
At the second iteration, each node
nodes, by using the FastReplica in the
small algorithm.
At the second iteration, each node
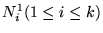 of group
of group
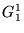 can serve as the origin node propagating file
can serve as the origin node propagating file  to another
group
to another
group 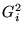 .
Thus in two iterations, file
.
Thus in two iterations, file  can be replicated to
can be replicated to 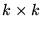 nodes. Correspondingly, in three iterations, file
nodes. Correspondingly, in three iterations, file 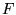 can be
replicated to
can be
replicated to
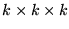 nodes.
The general FastReplica algorithm is based on the reasoning
described above. Let the problem consist in replicating file
nodes.
The general FastReplica algorithm is based on the reasoning
described above. Let the problem consist in replicating file 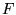 across nodes
across nodes
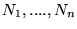 and let
and let
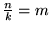 . Then all
the nodes are partitioned into
. Then all
the nodes are partitioned into 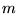 groups:
groups:
where each group has 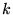 nodes.
Any number
nodes.
Any number 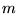 can be represented as
can be represented as
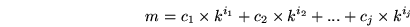 |
(8) |
where
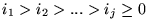 and
and
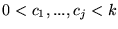 .
Practically, it is a
.
Practically, it is a 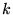 -ary representation of a number
-ary representation of a number 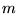 . This
representation defines the rules for constructing the tree structure
similar to the one shown in Figure 6. In
particular, the height of such a tree is
. This
representation defines the rules for constructing the tree structure
similar to the one shown in Figure 6. In
particular, the height of such a tree is 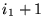 , and it defines the
number of iterations in the general FastReplica algorithm.
>From this representation, the rules for constructing the corresponding
distribution lists of nodes are straightforward. We omit the technical
details of the distribution lists construction in order to keep the
description of the overall algorithm concise.
If the targeted number
, and it defines the
number of iterations in the general FastReplica algorithm.
>From this representation, the rules for constructing the corresponding
distribution lists of nodes are straightforward. We omit the technical
details of the distribution lists construction in order to keep the
description of the overall algorithm concise.
If the targeted number 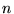 of nodes for a file replication
is not a multiple of
of nodes for a file replication
is not a multiple of 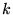 , i.e.
, i.e.
where 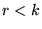 , then there is one
``incomplete'' group
, then there is one
``incomplete'' group 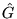 with
with 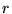 nodes in it. The best way to
deal with this group is to arrange it to be a leaf-group in the shortest
subtree. Let
nodes in it. The best way to
deal with this group is to arrange it to be a leaf-group in the shortest
subtree. Let
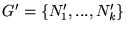 be a
replication group in the shortest subtree.
be a
replication group in the shortest subtree.
Figure 7:
Communications between the nodes of regular
replication group 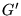 and incomplete replication group
and incomplete replication group
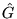 : special step.
: special step.
 |
The communications between groups 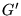 and
and 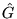 follow a
slightly different file exchange protocol. All the nodes in
follow a
slightly different file exchange protocol. All the nodes in
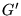 have already received all subfiles
have already received all subfiles
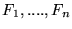 comprising the entire original file
comprising the entire original file 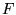 . Each node
. Each node 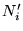 of
group
of
group 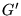 opens
opens 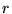 concurrent network connections to all
concurrent network connections to all 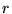 nodes of group
nodes of group 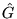 for transferring its subfile
for transferring its subfile 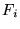 as shown
in Figure 7. In this way, at the end of this step,
each node of group
as shown
in Figure 7. In this way, at the end of this step,
each node of group 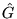 has all subfiles
has all subfiles
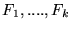 of
the original file
of
the original file 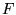 . We will denote this step as a special step.
Example. Let
. We will denote this step as a special step.
Example. Let 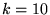 . How many algorithm iterations are required to
replicate the original file to 1000 nodes? Using Formula (8)
above, we derive the following representation for 1000 nodes:
. How many algorithm iterations are required to
replicate the original file to 1000 nodes? Using Formula (8)
above, we derive the following representation for 1000 nodes:
Thus, in three algorithm iterations (
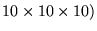 , the
original file can be replicated among all 1000 nodes. At each
iteration, the replication process follows FastReplica in the
small, i.e. the iteration consists of 2 steps, each used
for transferring the
, the
original file can be replicated among all 1000 nodes. At each
iteration, the replication process follows FastReplica in the
small, i.e. the iteration consists of 2 steps, each used
for transferring the 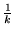 -th portion of the original file
-th portion of the original file 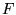 .
Let Multiple Unicast follow a similar recursive replication tree
as the one defined above in general FastReplica and shown in
Figure 6, with the only difference being that
communications between the origin nodes and the recipient nodes follow
the Multiple Unicast schema, i.e. the origin node transfers the
entire file
.
Let Multiple Unicast follow a similar recursive replication tree
as the one defined above in general FastReplica and shown in
Figure 6, with the only difference being that
communications between the origin nodes and the recipient nodes follow
the Multiple Unicast schema, i.e. the origin node transfers the
entire file 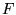 to the corresponding recipient nodes by simultaneously
using
to the corresponding recipient nodes by simultaneously
using 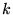 concurrent network connections. Thus, in three algorithm
iterations, by using Multiple Unicast recursively, the original
file can be replicated among 1000 nodes.
concurrent network connections. Thus, in three algorithm
iterations, by using Multiple Unicast recursively, the original
file can be replicated among 1000 nodes.


Next: 3.5 Reliable FastReplica Algorithm
Up: 3 FastReplica Algorithm
Previous: 3.3 Preliminary Performance Analysis

