Simulation Analysis of ALMI Multicast Tree Efficiency

While ALMI achieves group communication without relying on network layer multicast support and reduces the control load associated with group set-up and maintainance, it is bound to exhibit lower transmission efficiency since nodes on the distribution tree have to be ALMI capable and, thus currently confined to end hosts. Moreover, packet processing and forwarding at the application layer typically incurs higher delay when compared to router processing at the IP layer. In this section we investigate the extent of these ALMI performance constraints by conducting experiments which compare ALMI to IP multicast. Results obtained provide insight onto the trade-offs associated with ALMI and allow us to decide the applicability of ALMI for specific applications and deployment settings.

We examine the relative cost of an ALMI tree to those of source-rooted shortest path multicast trees as well the cost of a mesh of unicast connections which would have to be used in the absence of any multicast support. Trees are generated and costs computed over a set of random graphs with a variable number of multicast group members. The algorithms for generating random graphs are similar to those in [19], where a connected graph is generated with a specified edge connectivity probability.

In comparing the cost of an ALMI multicast tree to that of source-rooted shortest path multicast trees we note that since ALMI constructs a shared multicast tree, the cost of distributing data is the same independently of the location of the sender(s). However, this property does not hold for source-rooted trees, in which data originating at different nodes will traverse paths of differing cost to reach all group members. Therefore, to achieve a meaningful comparison, the cost of an ALMI multicast tree is compared with the average cost of all shortest path trees rooted at each group member.

Figure 3: Cost Comparison of ALMI MST and Shortest Path Tree in Random Graph

As mentioned in Section 2, ALMI provides a mechanism to further reduce control traffic load by allowing members to collect delay measurements to only a subset of other group members. Obviously, performing the MST calculation on a (connected) subgraph results in a sub-optimal ALMI distribution tree. In this section, we analyze quantitatively the impact of this mechanism in terms of how much it increases the cost of the actual ALMI multicast tree. The cost of an ALMI tree is defined to be the sum of delays on each link of the shared multicast tree; all link delays are assumed to be symmetric.

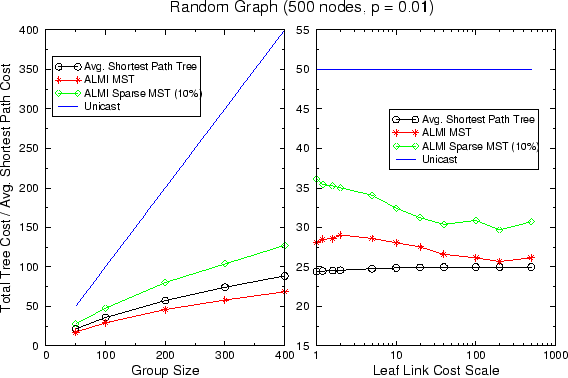
Figures 3 and 4 depict multicast tree cost in a random graph and a transit-stub graph, respectively. Each data point is derived by averaging over the results of 10 graphs. Random graphs in Figure 3 consist of 500 nodes with an average node degree of 5, and transit-stub graphs in Figure 4 consist of about 6000 nodes, with an average node degree of 3. More details about the formation of transit-stub graphs can be found in [19]. Link costs are uniformly distributed in the interval $[0,1]$.

Figure 4: Cost Comparison of ALMI MST and Shortest Path Tree in Transit-Stub Graph

In both figures, the x-axis of the graph on the left depicts multicast group size; groups of variable size are formed by selecting a random subset of network nodes as group members. It is assumed that every network node can be co-located with a host. The graphs on the left plot the average cost of all source-rooted trees, one for each multicast group node, the ALMI MST cost and the cost of a mesh of $O(n^2)$ unicast connections among all group members. We also compute the cost of an ALMI multicast tree calculated from incomplete information, denoted as ``ALMI sparse MST''. This tree corresponds to the case where every ALMI node monitors the delay to just 10% of the total number of group nodes.

We first concentrate on the results depicted in the left graphs of figures 3 and 4. It is interesting to observe that for the random graph, at all group sizes the ALMI MST cost is smaller than the average source-based tree cost. This is essentially due to the fact that an ALMI multicast tree is an MST tree; optimal source based trees are computed based on information local to each node and, therefore, are not globally optimal. On the other hand, in a transit-stub graph, the ALMI multicast tree is about 20% more expensive. This difference is due to the distinct characteristics of the two types of graphs. Since an ALMI multicast tree consists of a collection of unicast paths between hosts, some network links will be typically traversed multiple times. In a transit-stub graph, since hosts reside in stub networks, the links between transit domains and stub domains will most certainly be traversed multiple times, whereas in the random graph topology, since hosts are co-located with network nodes and uniformly distributed throughout the graph, the number of such links are fewer, hence lowering the cost of the ALMI multicast tree. Finally, as expected, the ALMI sparse MST has a higher total cost since it is derived using a subset of link metrics. Still, the cost difference in all cases is within 50%, which could be considered a reasonable price to pay for a 90% reduction in performance monitoring traffic.

Thus far, we have assumed that all network links have equal cost and that hosts are co-located with network nodes; in other words host are attached to the network with zero cost. In practice, however, this assumption might not be accurate; typically ``last mile'' links have lower bandwidth and thus result in higher delays and MST costs. Higher ``last mile'' costs could adversely impact ALMI, since all data flows in and out of non-leaf nodes in the ALMI tree at least twice and hence, the cost of link connecting hosts to a network aggregation point will contribute more to the total tree cost. In the right side graphs of Figure 3 and 4, we plot tree costs against the cost of the ``last-mile'' links. We include the same comparisons; ALMI MST, ALMI ``sparse MST'', average of all shortest path trees and meshed unicast connections. In this simulation, multicast group size is fixed to 50 and the ``last-mile'' link cost is uniformly distributed between 0 and $scale$, shown on the x-axis.

The results demonstrate that, even for a moderate group size of 50 members, the benefit of ALMI over pure unicast is still significant, reducing tree cost to only half. Furthermore, it is observed that as the cost of ``last-mile'' links increases, ALMI multicast tree cost decreases and approaches the cost of the average shortest path tree. This is due to the fact that MST calculation results in a tree which tends to prefer inclusion of low-cost links. This is similar to the behavior that would be observed if servers were deployed in the network to help relay data to other parts of the network. Overall, the simulation clearly shows the advantage of an ALMI multicast tree over $O(n^2)$ unicast connections. The fact that ALMI is almost as efficient as the shortest path trees even in the presence of incomplete measurements, argues that it is a rather attractive solution for many multicast applications.

In this simulation, we have focused on comparison of ALMI multicast tree with source-rooted shortest path trees. Compliment to SPTs, shared multicast tree, as constructed from CBT [1] and PIM-SM [7] optimizes the total cost of the multicast tree. Although it is known that finding the optimal center for the multicast group is an NP-complete problem, there are heuristic placement strategies to select one of the group member or network node to be the core. In [18], it shows that a resulting shared multicast tree from a feasible heuristic method has an average cost of 95% of the cost of shortest path tree for a varied number of group sizes, average node degree and different node distributions. Therefore, we infer that the cost difference between ALMI multicast tree and CBT or PIM-SM will be comparably small as well.