


Next: Impact of Packet Size
Up: Impact of DCF on
Previous: Impact of DCF on
Impact of Rate Diversity
To understand the impact of rate diversity, let's assume that each node
uses the same packet size, i.e.
 , si = sj.
Therefore,
based on Equations 2 and 3,
, si = sj.
Therefore,
based on Equations 2 and 3,
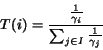 |
(5) |
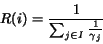 |
(6) |
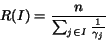 |
(7) |
Equation 6 clearly shows that the throughput of each node
i is the same. Thus, under these
conditions, DCF achieves throughput-based fairness. Observe, however,
the amount of
throughput is dependent on the baseline throughputs of all nodes in I,
which in turn depend on their data rates and packet sizes.
The channel occupancy time T(i) of node i is inversely proportional
to the baseline throughput of node i, which increases with the
increase in transmission rate. Thus, as expected, nodes with slower
data rates occupy the channel much longer than those with higher data
rates, leading to degradation in the overall network performance.


Next: Impact of Packet Size
Up: Impact of DCF on
Previous: Impact of DCF on
Godfrey Tan
2004-05-04

![]() , si = sj.
Therefore,
based on Equations 2 and 3,
, si = sj.
Therefore,
based on Equations 2 and 3,