 |

We have devised a new wait-free IPC mechanism that is less computationally complex than Chen's algorithm. It, however, trades off time for space complexity, requiring approximately twice the buffer space. Hence, it is called the Double Buffer algorithm.
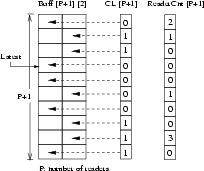
The basic constructs of the Double Buffer algorithm are shown in Figure 5, and the algorithm is summarized in Figure 6. A two-dimensional shared message buffer, Buff[][], has (P + 1) rows, where P is the number of reader tasks. Each row has two buffers. Associated with each row i is a usage count, ReaderCnt[i], representing the number of readers currently using either buffer in the row, and a flag, Cl[i], indicating which of the two buffers is more current. A variable, Latest, points to the row containing the most recently written data. A reader task first reads Latest, and indicates it is using the row by incrementing the usage count. It then reads the buffer indicated by the row's Cl flag, and decrements the row's usage count when it finishes reading. Note that the increment and decrement operate directly on memory variables and must be atomic. This is commonly available on modern processors, including the x86 architecture.
The writer is fairly straightforward. It first scans ReaderCnt[], and selects a row that is not being used by the readers. It then writes to the buffer that was least recently written in the selected row (i.e., opposite to the one indicated by the row's Cl flag). We will see why this is necessary shortly. Finally, it updates the row's Cl flag to point to the newly-written buffer, and sets Latest to the row that contains this buffer. In case each reader is concurrently reading from a unique row, this algorithm requires (P + 1) rows for the writer to work correctly, where P is the number of readers. As each row has 2 buffers, the space required for the message buffer array is 2(P + 1).
To see the correctness of the algorithm, let us consider the possible interference scenarios. The writer can only interfere with the reader when they both choose to use the same row. This can only occur in two cases. The first case can occur when a reader is interrupted after it has chosen a row (after line 1), but before it updates the use count (before line 2). The writer then executes, and can potentially choose the same row as the reader. The second case occurs when the writer is interrupted after it has chosen a row (after line 7). If this row happens to be Latest, then the reader can also choose to read from this same row. So, it is possible for the readers and the writer to select the same row i. However, the reader will read from the buffer indicated by Cl[i], while the writer will use the opposite one. As the writer updates Cl[i] only after the complete message is written, and the reader always increments the use count before reading Cl[i], we can guarantee that the writer and readers cannot interfere with each other in this algorithm, even if they happen to use the same row.
The Double Buffer algorithm is less computationally complex than Chen's algorithms, but has a space requirement twice that of the original Chen's algorithm. In the next section, we use our transformation technique to improve the Double Buffer algorithm. As we will see in Section 4, the number of buffers required by the transformed Double Buffer algorithm is usually comparable to, if not less than, the original Chen's algorithm.