To investigate how well the clusters found for each test represent real use-model properties of the computer systems in the sample, we used external information on each computer system in our sample, that included specifications of installed hardware and software components and their configuration parameters. The information was represented as binary features of the computer systems. For each cluster in each test, we searched for the binary feature that had the highest mutual information with the property of belonging to the cluster. In Figure
![[*]](crossref.png)
we list the highest mutual information found in each test. The clusters in the Spearman feature-set are consistently more correlated with actual properties of the computer systems. Since there are usually several such features and their interpretation is highly technical, we do not list here the actual features for each cluster.
The cluster with the highest mutual information coefficient in all our
tests is one found in the Spearman test conducted with three
clusters. It has mutual information of 0.9 with the best-correlated
features of the systems; it was therefore easiest to find its
`meaning'. The features that were
most highly correlated with this cluster indicated that several
services related to IBM Director are installed on the computer systems in this cluster,
but not on computer systems that are not in this cluster.
IBM Director is a suite of tools
for managing computer systems that affects the behavior of many
components in the system. It is therefore reasonable that it would
significantly affect the log behavior of systems.
An interesting
addition to our log ranking tool would be the ability to automatically
generate and display a meaningful description of the cluster to which the inspected system belongs.
Figure:
The maximal mutual information between a cluster and a binary feature found in each of the clustering tests.
|
|
If the clusters truly represent sets of systems that are more
homogeneous in terms of their log behavior as compared to the entire
set of computer systems, then we expect the average score of messages
in a ranked log to be lower when the score is computed using the
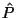
of the cluster, compared to the average score computed using
the
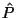
of the entire population. Figure
![[*]](crossref.png)
compares, for each of the clustering tests, the average difference in
the average score of all the system logs in our dataset, between the
cluster-based scoring and the non-cluster-based scoring. The
Spearman-based clustering achieved the largest lowering of the
score. We calculated the statistical significance of the results using
a paired T-test, with resulting p-values of 0 in all cases.
Figure:
The change in the mean score (in a scale of 0-100) of messages in all machines, when calculated by the cluster the machine belongs to instead of the entire set of machines.
![\fbox{
\includegraphics[width=0.9\linewidth,keepaspectratio]{diff2.png}
}](diff2.png) |
No single message was found to have a high level of mutual information
with the clusters that were found in any of the tests. This is
expected, as most messages appear in only a small fraction of the
logs. Nonetheless, to visualize the way different messages are
manifested in different clusters, we plot for each cluster the probability of each
message appearing in the cluster versus its probability of appearing
in the entire dataset. For a cluster that is highly distinctive among
messages, a relatively large number of messages would appear far from the diagonal.
Figure:
The probability of each message in the cluster versus its probability in the entire sample, with 3 clusters. Each row depicts the three clusters of one feature-set.
![\fbox{
\includegraphics[width=0.9\linewidth]{probPlot3clustersSpearmanLinearNocorr2.png}}](probPlot3clustersSpearmanLinearNocorr2.png) |
Plot
![[*]](crossref.png)
shows the case of three clusters. The
Spearman-based approach yields the most distinctive clusters. To
numerically estimate this difference, Table
![[*]](crossref.png)
shows
the mean ratio between the probability of a message appearing in a cluster and its probability within the entire sample set, averaged over all the clusters in each test.
Table:
The mean of the ratio between the probability of each message in each cluster and its probability in the general population. For ratios higher than 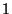 their inverse is taken. A smaller mean ratio implies a more distinctive clustering.
their inverse is taken. A smaller mean ratio implies a more distinctive clustering.
| Clusters |
Spearman |
Pearson |
FM |
| 2 |
0.65 |
0.77 |
0.82 |
| 3 |
0.62 |
0.77 |
0.77 |
| 4 |
0.57 |
0.74 |
0.78 |
| 5 |
0.57 |
0.75 |
0.76 |
|

![[*]](crossref.png) shows the histogram of pairwise distances in each of the three representations we tested.
It is easy to see that the Spearman-based representation arranges the data in a bimodal way, much more so than the other two representations do.
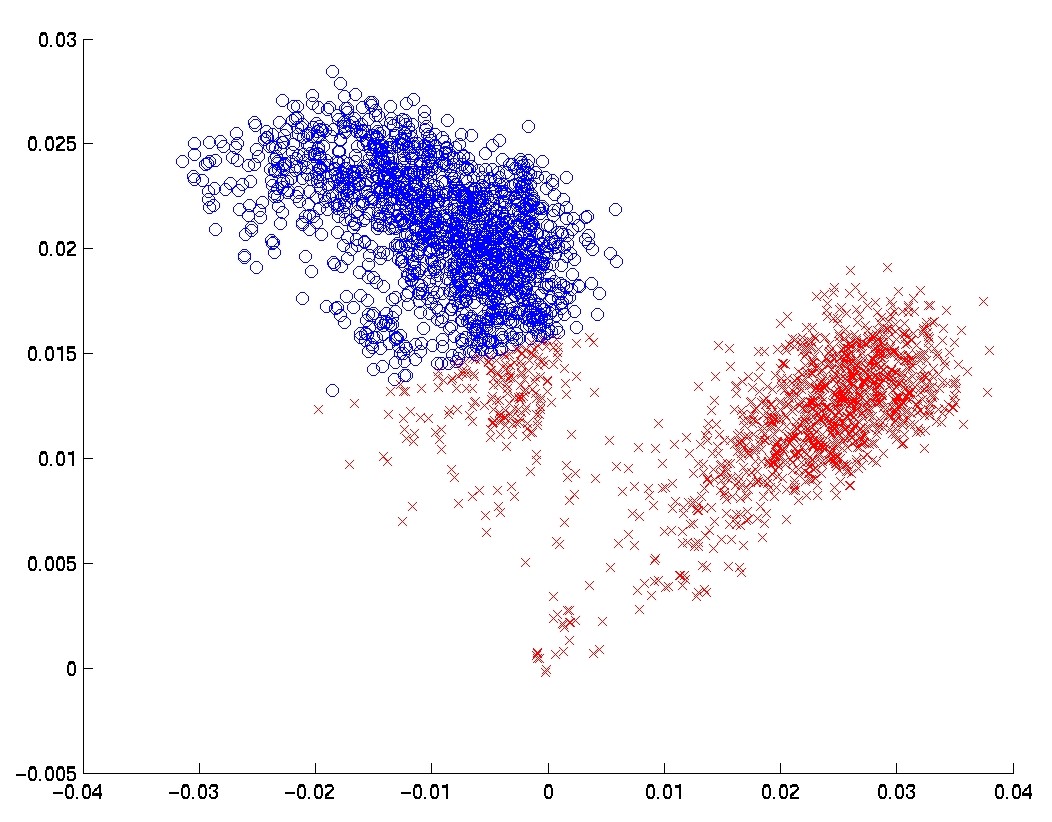
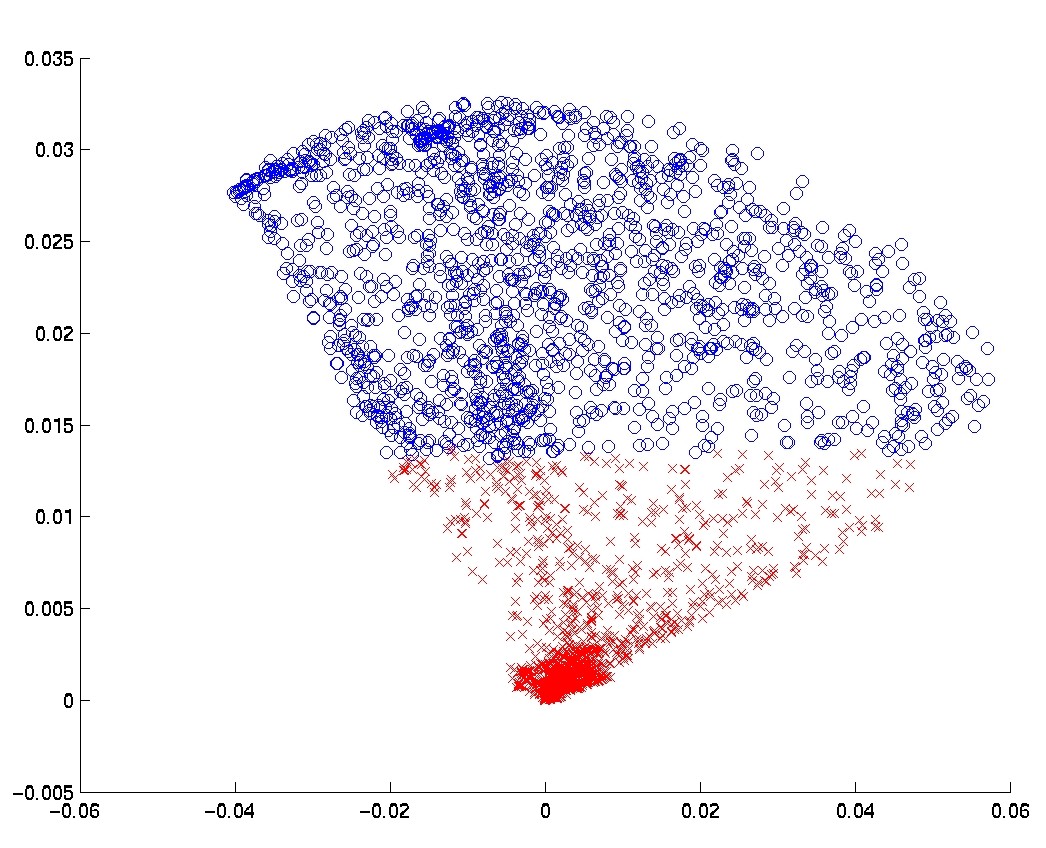
Another way to visualize the spatial structure of the samples in the two first feature-sets is to plot the two largest eigenvectors of the resulting correlation matrices on the plane, giving the first two Principal Components of the sample points. In Figure
shows the histogram of pairwise distances in each of the three representations we tested.
It is easy to see that the Spearman-based representation arranges the data in a bimodal way, much more so than the other two representations do.
Another way to visualize the spatial structure of the samples in the two first feature-sets is to plot the two largest eigenvectors of the resulting correlation matrices on the plane, giving the first two Principal Components of the sample points. In Figure ![[*]](crossref.png) , this plot is shown for the Spearman-based and for the Pearson-based feature-sets.4 Much more structure is revealed in the Spearman-based feature-set. The division into two clusters by the k-means algorithm is also depicted in the plot.
Note that since this plot is only a two dimensional projection of the high dimensional space, the partition of the data
into clusters may appear as if it were sub-optimal in this plot.
, this plot is shown for the Spearman-based and for the Pearson-based feature-sets.4 Much more structure is revealed in the Spearman-based feature-set. The division into two clusters by the k-means algorithm is also depicted in the plot.
Note that since this plot is only a two dimensional projection of the high dimensional space, the partition of the data
into clusters may appear as if it were sub-optimal in this plot.

 To investigate how well the clusters found for each test represent real use-model properties of the computer systems in the sample, we used external information on each computer system in our sample, that included specifications of installed hardware and software components and their configuration parameters. The information was represented as binary features of the computer systems. For each cluster in each test, we searched for the binary feature that had the highest mutual information with the property of belonging to the cluster. In Figure
To investigate how well the clusters found for each test represent real use-model properties of the computer systems in the sample, we used external information on each computer system in our sample, that included specifications of installed hardware and software components and their configuration parameters. The information was represented as binary features of the computer systems. For each cluster in each test, we searched for the binary feature that had the highest mutual information with the property of belonging to the cluster. In Figure ![[*]](crossref.png) we list the highest mutual information found in each test. The clusters in the Spearman feature-set are consistently more correlated with actual properties of the computer systems. Since there are usually several such features and their interpretation is highly technical, we do not list here the actual features for each cluster.
The cluster with the highest mutual information coefficient in all our
tests is one found in the Spearman test conducted with three
clusters. It has mutual information of 0.9 with the best-correlated
features of the systems; it was therefore easiest to find its
`meaning'. The features that were
most highly correlated with this cluster indicated that several
services related to IBM Director are installed on the computer systems in this cluster,
but not on computer systems that are not in this cluster.
IBM Director is a suite of tools
for managing computer systems that affects the behavior of many
components in the system. It is therefore reasonable that it would
significantly affect the log behavior of systems.
An interesting
addition to our log ranking tool would be the ability to automatically
generate and display a meaningful description of the cluster to which the inspected system belongs.
we list the highest mutual information found in each test. The clusters in the Spearman feature-set are consistently more correlated with actual properties of the computer systems. Since there are usually several such features and their interpretation is highly technical, we do not list here the actual features for each cluster.
The cluster with the highest mutual information coefficient in all our
tests is one found in the Spearman test conducted with three
clusters. It has mutual information of 0.9 with the best-correlated
features of the systems; it was therefore easiest to find its
`meaning'. The features that were
most highly correlated with this cluster indicated that several
services related to IBM Director are installed on the computer systems in this cluster,
but not on computer systems that are not in this cluster.
IBM Director is a suite of tools
for managing computer systems that affects the behavior of many
components in the system. It is therefore reasonable that it would
significantly affect the log behavior of systems.
An interesting
addition to our log ranking tool would be the ability to automatically
generate and display a meaningful description of the cluster to which the inspected system belongs.
![\fbox{
\includegraphics[width=0.8\linewidth,keepaspectratio]{mi3.png}
}](mi3.png)
![[*]](crossref.png) compares, for each of the clustering tests, the average difference in
the average score of all the system logs in our dataset, between the
cluster-based scoring and the non-cluster-based scoring. The
Spearman-based clustering achieved the largest lowering of the
score. We calculated the statistical significance of the results using
a paired T-test, with resulting p-values of 0 in all cases.
compares, for each of the clustering tests, the average difference in
the average score of all the system logs in our dataset, between the
cluster-based scoring and the non-cluster-based scoring. The
Spearman-based clustering achieved the largest lowering of the
score. We calculated the statistical significance of the results using
a paired T-test, with resulting p-values of 0 in all cases.
![\fbox{
\includegraphics[width=0.9\linewidth,keepaspectratio]{diff2.png}
}](diff2.png)
![\fbox{
\includegraphics[width=0.9\linewidth]{probPlot3clustersSpearmanLinearNocorr2.png}}](probPlot3clustersSpearmanLinearNocorr2.png)
![[*]](crossref.png) shows the case of three clusters. The
Spearman-based approach yields the most distinctive clusters. To
numerically estimate this difference, Table
shows the case of three clusters. The
Spearman-based approach yields the most distinctive clusters. To
numerically estimate this difference, Table ![[*]](crossref.png) shows
the mean ratio between the probability of a message appearing in a cluster and its probability within the entire sample set, averaged over all the clusters in each test.
shows
the mean ratio between the probability of a message appearing in a cluster and its probability within the entire sample set, averaged over all the clusters in each test.