| Rank |
Times |
Source |
Message |
|---|
| 1 |
10 |
ViperW2K |
The device,
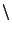 Device Device
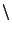 Tape1, has a bad block. Tape1, has a bad block. |
| 2 |
4 |
Oracle.cq1 |
Audit trail: ACTION : 'CONNECT' DATABASE USER: '/' PRIVILEGE : SYSOPER ... |
| 3 |
1 |
SAPCQ1_20 |
SAP Basis System: Run-time error "TIME_OUT" occurred |
| 4 |
1014 |
SAPCQ120 |
SAP Basis System: Transaction Canceled 00 158 ( ) |
| 5 |
1 |
MRxSmb |
Delayed Write Failed ...may be caused by a failure of your computer hardware ... |
| 6 |
8 |
ql2300 |
The device,
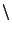 Device Device
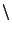 Scsi Scsi
 ql23002, did not respond within the timeout period. ql23002, did not respond within the timeout period. |
| 7 |
54 |
DnsApi |
The system failed to register pointer (PTR) resource records (RRs) for network adapter ... |
| 8 |
1 |
Kerberos |
The kerberos subsystem encountered a PAC verification failure. ... |
| 9 |
1 |
Windows Update Agent |
Installation Failure: Windows failed to install the following update with error ... |
| 10 |
1 |
NETLOGON |
The Netlogon service could not read a mailslot message from The system ... |

![[*]](crossref.png) , which was generated from one of the samples in our dataset.
, which was generated from one of the samples in our dataset.