

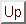

: Loss Probability Estimation
: Potential Bandwidth Estimation
: Downstream Bandwidth estimation in
Downstream Bandwidth estimation in presence of RTS/CTS
With the  handshake, each data frame transmission incurs a total delay (
handshake, each data frame transmission incurs a total delay (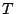 ) given by Eq. (5), the sum of delays incurred by the
) given by Eq. (5), the sum of delays incurred by the 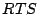 ,
, 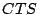 , data and
, data and
 frames respectively.
frames respectively.
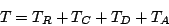 |
(5) |
Since the frame transmission rules
for an  and beacon frames are the same, the delay incurred by an
and beacon frames are the same, the delay incurred by an  frame can be
estimated using Eq. (6), as the sum of
frame can be
estimated using Eq. (6), as the sum of  and transmission delay
(all MAC control frames are transmitted at the base rate).
and transmission delay
(all MAC control frames are transmitted at the base rate).
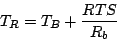 |
(6) |
Upon receiving a 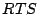 frame, a receiver waits a duration of time equal to
frame, a receiver waits a duration of time equal to 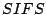 and transmits a
and transmits a 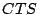 frame, again at the base rate
frame, again at the base rate  .
The
.
The 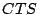 frame is transmitted at the base rate
frame is transmitted at the base rate  and its delay is given by:
and its delay is given by:
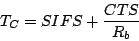 |
(7) |
The delay incurred by the data frame is given by:
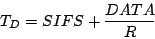 |
(8) |
Lastly, the computation of 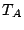 remains the same across both schemes and is
given by Eq. (3). The potential bandwidth
remains the same across both schemes and is
given by Eq. (3). The potential bandwidth 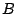 is then obtained using Eq. (4).
is then obtained using Eq. (4).

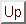

: Loss Probability Estimation
: Potential Bandwidth Estimation
: Downstream Bandwidth estimation in
