Check out the new USENIX Web site. next up previous
Next: The Key Expansion Up: The public-key coprocessor based Previous: The MixColumn transformation

The inverse MixColumn transformation

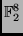The inverse MixColumn transformation requires also a matrix multiplication in the field $ \mathbb{F}_2^8$. In an 8-bit CPU, this can be implemented in an efficient way for each column as follows:
$\displaystyle y_0$ $\displaystyle =$ $\displaystyle 0e * x_0 \oplus 0b * x_1 \oplus 0d * x_2 \oplus 09 * x_3$  
$\displaystyle y_1$ $\displaystyle =$ $\displaystyle 09 * x_0 \oplus 0e * x_1 \oplus 0b * x_2 \oplus 0d * x_3$  
$\displaystyle y_2$ $\displaystyle =$ $\displaystyle 0d * x_0 \oplus 09 * x_1 \oplus 0e * x_2 \oplus 0b * x_3$  
$\displaystyle y_3$ $\displaystyle =$ $\displaystyle 0b * x_0 \oplus 0d * x_1 \oplus 09 * x_2 \oplus 0e * x_3.$  

After reordering the equations we get:
$\displaystyle y_0$ $\displaystyle =$ $\displaystyle 0e * x_0 \oplus 0b * x_1 \oplus 0d * x_2 \oplus 09 * x_3$  
$\displaystyle y_1$ $\displaystyle =$ $\displaystyle 0e * x_1 \oplus 0b * x_2 \oplus 0d * x_3 \oplus 09 * x_0$  
$\displaystyle y_2$ $\displaystyle =$ $\displaystyle 0e * x_2 \oplus 0b * x_3 \oplus 0d * x_0 \oplus 09 * x_1$  
$\displaystyle y_3$ $\displaystyle =$ $\displaystyle 0e * x_3 \oplus 0b * x_0 \oplus 0d * x_1 \oplus 09 * x_2.$  

As for the MixColumn, the inverse transformation (needed for decryption) can also be defined to operate on the 16 bytes of the state in parallel. The implementation is based on the previous definition of the $ {\tt xtime}$ operation:
$\displaystyle t_1$ $\displaystyle =$ $\displaystyle {\tt xtime}($state$\displaystyle )$  
$\displaystyle %% ; 02 * state t_2$ $\displaystyle =$ $\displaystyle {\tt xtime}(t_1)$  
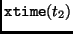$\displaystyle %%; 04 * state t_3$ $\displaystyle =$ $\displaystyle {\tt xtime}(t_2)$  
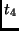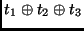$\displaystyle %%; 08 * state t_4$ $\displaystyle =$ $\displaystyle t_1 \oplus t_2 \oplus t_3$  
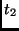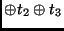$\displaystyle %% ; % 0e * state t_2$ $\displaystyle =$ state$\displaystyle \oplus t_2 \oplus t_3$  
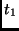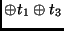$\displaystyle %% ; 0d * state t_1$ $\displaystyle =$ state$\displaystyle \oplus t_1 \oplus t_3$  
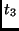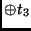$\displaystyle %% ; 0b * state t_3$ $\displaystyle =$ state$\displaystyle \oplus t_3$  
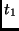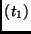$\displaystyle %% ; 09 * state t_1$ $\displaystyle =$ RotWord$\displaystyle (t_1)$  
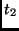$\displaystyle %% ; 1-byte left rotation of 0b * state t_2$ $\displaystyle =$ RotWord$\displaystyle ($RotWord$\displaystyle (t_2))$  
$\displaystyle %% ; 2-byte left rotation of 0d * state t_3$ $\displaystyle =$ RotWord$\displaystyle ($RotWord$\displaystyle ($RotWord$\displaystyle (t_3)))$  
$\displaystyle <tex2html_comment_mark>21$   state $\displaystyle =$ $\displaystyle t_1 \oplus t_2 \oplus t_3 \oplus t_4 <tex2html_comment_mark>22$  

The total number of registers needed for the implementation of the inverse transformation in the coprocessor is 5, where 4 temporal registers are used for intermediate results and one other register for the state itself. Another way to implement the inverse MixColumn transformation is by definition of the following two new operations:
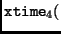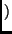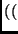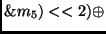$\displaystyle {\tt xtime}_4 ($state$\displaystyle )$ $\displaystyle =$ $\displaystyle (($state$\displaystyle \& m_5) << 2) \oplus$  
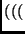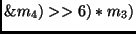    $\displaystyle ((($state$\displaystyle \& m_4) >> 6) * m_3)$  
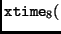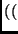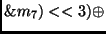$\displaystyle {\tt xtime}_8 ($state$\displaystyle )$ $\displaystyle =$ $\displaystyle (($state$\displaystyle \& m_7) << 3) \oplus$  
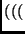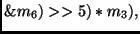    $\displaystyle ((($state$\displaystyle \& m_6) >> 5) * m_3),$  

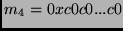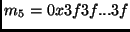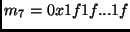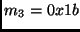where $ m_4 = 0xc0c0...c0$ (16 bytes), $ m_5 = 0x3f3f...3f$ (16 bytes), $ m_6 = 0xe0e0...e0$ (16 bytes), $ m_7 = 0x1f1f...1f$ (16 bytes) and $ m_3 = 0x1b$. Therefore, the implementation of the inverse MixColumn transformation can be redefined as follows:
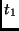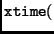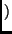$\displaystyle t_1$ $\displaystyle =$ $\displaystyle {\tt xtime}($state$\displaystyle )$  
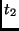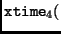$\displaystyle %%; 02 * state t_2$ $\displaystyle =$ $\displaystyle {\tt xtime}_4 ($state$\displaystyle )$  
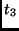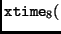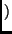$\displaystyle %% ; 04 * state t_3$ $\displaystyle =$ $\displaystyle {\tt xtime}_8 ($state$\displaystyle )$  
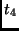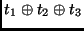$\displaystyle %% ; 08 * state t_4$ $\displaystyle =$ $\displaystyle t_1 \oplus t_2 \oplus t_3$  
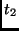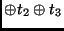$\displaystyle %% ; 0e * state t_2$ $\displaystyle =$ state$\displaystyle \oplus t_2 \oplus t_3$  
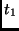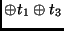$\displaystyle %% ; 0d * state t_1$ $\displaystyle =$ state$\displaystyle \oplus t_1 \oplus t_3$  
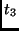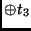$\displaystyle %% ; 0b * state t_3$ $\displaystyle =$ state$\displaystyle \oplus t_3$  
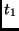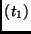$\displaystyle %% ; 09 * state t_1$ $\displaystyle =$ RotWord$\displaystyle (t_1)$  
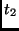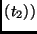$\displaystyle %% ; 1-byte left rotation of 0b * state t_2$ $\displaystyle =$ RotWord$\displaystyle ($RotWord$\displaystyle (t_2))$  
$\displaystyle %% ; 2-byte left rotation of 0d * state t_3$ $\displaystyle =$ RotWord$\displaystyle ($RotWord$\displaystyle ($RotWord$\displaystyle (t_3)))$  
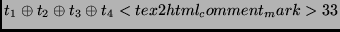$\displaystyle %% ; 3-byte left rot. of 09 * state state$ $\displaystyle =$ $\displaystyle t_1 \oplus t_2 \oplus t_3 \oplus t_4 <tex2html_comment_mark>33$  

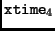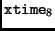The advantage of this second implementation is that the operations $ {\tt xtime}$, $ {\tt xtime}_4$ and $ {\tt xtime}_8$ can be calculated in parallel from the state, avoiding the sequence of the first implementation. M oreover, in the case that the AND operation is not available within the coprocessor, this second solution allows to precompute all the AND values within the standard CPU before loading the state into the coprocessor.
next up previous
Next: The Key Expansion Up: The public-key coprocessor based Previous: The MixColumn transformation
Roger Fischlin 2002-09-25