



Next: The AddRoundKey transformation
Up: The public-key coprocessor based
Previous: The inverse MixColumn transformation
The 16, 24 or 32 bytes of the key (depending on the key length) are loaded into the Key
register1 of the coprocessor (Key1 and Key2 registers for 256-bit keys).
Then, the next round key bytes are calculated with the following sequence of operations.
For a 128-bit key, perform the following sequence, and for each intermediate round do:
 |
 |
Rcon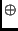 ByteSub ByteSub RotWord RotWord Key Key |
|
| Key |
 |
Key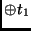 |
|
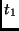 |
 |
Key |
|
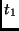 |
 |
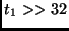 |
|
| Key |
 |
Key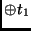 |
|
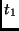 |
 |
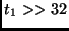 |
|
| Key |
 |
Key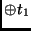 |
|
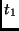 |
 |
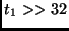 |
|
| Key |
 |
Key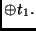 |
|
The
RotWord,
ByteSub operations are performed
by the standard CPU on the 4 rightmost bytes of the
Key register, then storing the result into the 4 leftmost bytes of 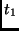 and clearing the other bytes.
Rcon is the 4-byte constant defined within the AES specification.
For a 256-bit key perform the following sequence, and for each intermediate ``even" round do:
and clearing the other bytes.
Rcon is the 4-byte constant defined within the AES specification.
For a 256-bit key perform the following sequence, and for each intermediate ``even" round do:
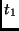 |
 |
Rcon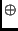 ByteSub ByteSub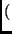 RotWord RotWord Key2 Key2 |
|
Key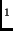 |
 |
Key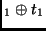 |
|
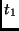 |
 |
Key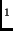 |
|
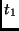 |
 |
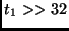 |
|
Key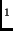 |
 |
Key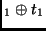 |
|
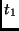 |
 |
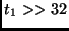 |
|
Key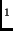 |
 |
Key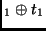 |
|
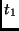 |
 |
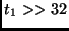 |
|
Key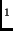 |
 |
Key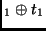 |
|
while every intermediate ``odd" round (except round 1) is done as:
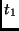 |
 |
ByteSub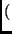 Key1 Key1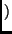 |
|
Key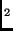 |
 |
Key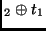 |
|
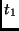 |
 |
Key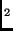 |
|
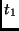 |
 |
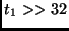 |
|
Key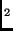 |
 |
Key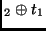 |
|
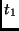 |
 |
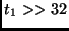 |
|
Key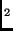 |
 |
Key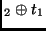 |
|
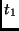 |
 |
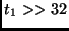 |
|
Key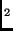 |
 |
Key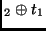 |
|
For 196-bit keys, the sequence gets more complicated as in that case,
new round key bytes are generated within a window of 6 bytes,
but round key bytes should be delivered at a rate of 4 bytes.
Basically, the process to generate the new round key bytes is similar to that for 128 bit keys,
but yet longer registers (24 bytes long) and/or an additional temporary register might be needed.
Totally, the number of registers needed for the implementation of the Key Expansion transformation
within the coprocessor is 2 (or at maximum 3 for keys longer than 16 bytes).



Next: The AddRoundKey transformation
Up: The public-key coprocessor based
Previous: The inverse MixColumn transformation
Roger Fischlin
2002-09-25
