



Next: The inverse MixColumn transformation
Up: The public-key coprocessor based
Previous: The public-key coprocessor based
The multiplication of columns (
MixColumn) is based on the
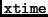 operation as defined within the AES specification.
It multiplies a byte of the so called state by 2 modulo the irreducible polynomial
operation as defined within the AES specification.
It multiplies a byte of the so called state by 2 modulo the irreducible polynomial
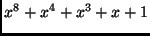 .
This operation is usually performed on a byte by left shifting the byte (multiplication by 2) and,
in case of overflow, xoring (addition modulo 2) with the hexadecimal value
.
This operation is usually performed on a byte by left shifting the byte (multiplication by 2) and,
in case of overflow, xoring (addition modulo 2) with the hexadecimal value 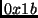 .
The MixColumn transformation requires matrix multiplication in the field
.
The MixColumn transformation requires matrix multiplication in the field
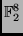 .
In an 8-bit CPU, this can be implemented in an efficient way for each column as follows:
.
In an 8-bit CPU, this can be implemented in an efficient way for each column as follows:
where 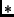 represents the
represents the
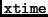 operation.
After re-ordering the equations we get:
operation.
After re-ordering the equations we get:
The
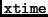 operation can be performed inside the coprocessor on the 16 bytes of the state in parallel
via the following formula:
operation can be performed inside the coprocessor on the 16 bytes of the state in parallel
via the following formula:
where
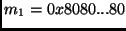 (16 bytes),
(16 bytes),
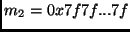 (16 bytes) and
(16 bytes) and
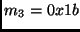 .
Here,
.
Here, 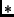 denotes the multiplication operation in
denotes the multiplication operation in
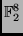 ,
,
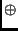 is the addition modulo 2,
is the addition modulo 2,
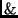 the AND operation and
the AND operation and
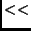 and
and 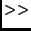 are the bit-left and bit-right shift operations respectively.
The
are the bit-left and bit-right shift operations respectively.
The
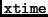 operation itself can be implemented inside the coprocessor with only two temporary registers,
as shown below:
operation itself can be implemented inside the coprocessor with only two temporary registers,
as shown below:
If the AND operation is not supported by the coprocessor,
it has to be done in the standard CPU before loading the state into the coprocessor's register.
Then, one has to load the result of the AND operations in both 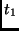 and
and 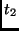 .
Based on the previous definition of the
.
Based on the previous definition of the
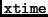 operation,
the whole
MixColumn transformation can be defined to operate on the 16 bytes of the state in parallel.
The implementation is based on the previous definition of the
operation,
the whole
MixColumn transformation can be defined to operate on the 16 bytes of the state in parallel.
The implementation is based on the previous definition of the
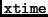 operation:
operation:
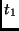 |
 |
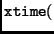 state state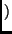 |
|
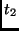 |
 |
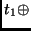 state state |
|
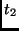 |
 |
RotWord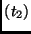 |
|
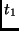 |
 |
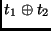 |
|
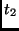 |
 |
RotWord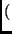 state state |
|
 |
 |
RotWord |
|
 |
 |
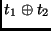 |
|
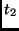 |
 |
RotWord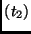 |
|
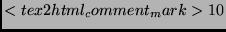 state state |
 |
 |
|
The total number of registers needed for the implementation of the
MixColumn transformation in the coprocessor is 3,
two temporal registers for the intermediate results and another for the state.
The
RotWord operation as defined in the AES specification has to be performed on every 4 bytes
of the state independently.
If it is not supported by the coprocessor, this operation must be done by the standard CPU,
accessing the internal coprocessor's registers.



Next: The inverse MixColumn transformation
Up: The public-key coprocessor based
Previous: The public-key coprocessor based
Roger Fischlin
2002-09-25
