
Next: Coalition-Resistance
Up: Group Signature Schemes and
Previous: Group Signature Schemes and
Our solution consists in using a smart card and a group-shared
private key. First of all, we must choose an ordinary signature
scheme (keys 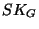 and
and 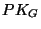 ) and a semantically secure
cryptosystem (keys
) and a semantically secure
cryptosystem (keys 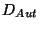 and
and 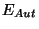 ), which is a
cryptosystem where the ciphertext does not leak any partial
information whatsoever about the plaintext that can be computed in
expected polynomial time (and consequently, it is a probabilist
cryptosystem). Then, the group manager computes keys in such a way
that he can keep secret private ones (
), which is a
cryptosystem where the ciphertext does not leak any partial
information whatsoever about the plaintext that can be computed in
expected polynomial time (and consequently, it is a probabilist
cryptosystem). Then, the group manager computes keys in such a way
that he can keep secret private ones (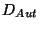 ) or distribute
them (
) or distribute
them (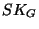 ) to members without knowing them (for example,
several group managers can share a discrete logarithm as the
private key). He publishes public keys (
) to members without knowing them (for example,
several group managers can share a discrete logarithm as the
private key). He publishes public keys (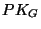 and
and
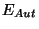 ).
).
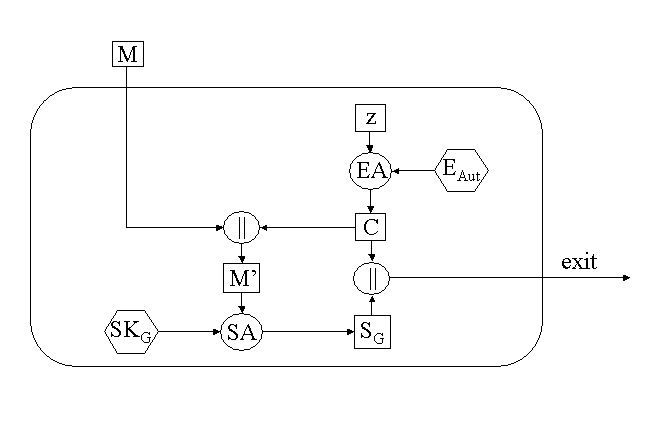
If Alice wants to become a new group member, she firstly has to
hold a smart card. Then, she has to obtain from the group manager
an identifier 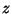 (which is unique and that identifies her) and
the shared private key
(which is unique and that identifies her) and
the shared private key 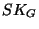 (which is common to all group
members). Alice's smart card also has access to all parameters so
as to use the cryptosystem (among which
(which is common to all group
members). Alice's smart card also has access to all parameters so
as to use the cryptosystem (among which  ) and the
signature scheme defined above. The group manager has to keep in
mind the link between the identifier (i.e.
) and the
signature scheme defined above. The group manager has to keep in
mind the link between the identifier (i.e. 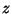 ) and the identity
of the group member (i.e. Alice).
) and the identity
of the group member (i.e. Alice).
When Alice wants to sign a message as a group member (see
Figure 1), she has to use her smart card. First, the
identifier 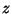 is encrypted (algorithm
is encrypted (algorithm 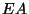 ) with the group
manager's public key
) with the group
manager's public key 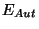 (so that the group manager is the
only one who can decrypt). Then the message
(so that the group manager is the
only one who can decrypt). Then the message 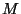 is concatenated
with this encrypted value
is concatenated
with this encrypted value 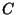 and the whole is signed with the
help of (algorithm
and the whole is signed with the
help of (algorithm 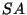 and) the shared private key
and) the shared private key 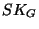 . As a
consequence, only group members can sign a message and everybody
is able to verify the signature with the associated public key
. As a
consequence, only group members can sign a message and everybody
is able to verify the signature with the associated public key
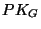 .
.
Figure 1:
Shared Private Key and Smart Card
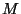 = Message = Message |
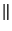 = Concatenation algorithm = Concatenation algorithm |
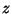 = Member's identifier = Member's identifier |
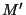 = Concatenation of = Concatenation of 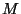 and and 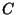 |
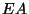 = Encryption algorithm = Encryption algorithm |
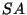 = Signature algorithm = Signature algorithm |
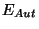 = GM's encryption key = GM's encryption key |
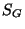 = Signature of the message = Signature of the message |
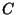 = Encryption of the identifier = Encryption of the identifier |
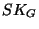 = Group-shared signature private key = Group-shared signature private key |
|
The verifier obtains the encrypted value 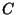 , the message
, the message 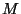 , and
the signature
, and
the signature 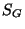 of the whole. He only has to verify the
signature to be sure that the message is sent by a group member
(because only group members possess the group-shared private key
used to compute the signature). The group manager can open the
signature by decrypting the identifier (with the key
of the whole. He only has to verify the
signature to be sure that the message is sent by a group member
(because only group members possess the group-shared private key
used to compute the signature). The group manager can open the
signature by decrypting the identifier (with the key
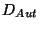 ).
).
It is important to note that the encryption scheme can either be
symmetric or asymmetric. Nevertheless, it must be probabilist. On
the contrary, it is necessary to use an (asymmetric) signature
scheme for obvious reasons.
This approach makes possible a very fast signature, since there is
only one encryption and one ordinary signature to compute.
Consequently, our solution is much better than previous ones in
terms of speed and memory and in terms of genericity (any
signature scheme can be employed).
Furthermore, it can be used in an on-line/off-line manner as
follows : first of all, the card precomputes several encrypted
values C in an off-line phase. Then, by using an on-line/off-line
signature scheme SA, the card can precompute some values in an
off-line phase, and later (in the on-line phase) produce group
signatures very quickly, for example by doing a single
multiplication if using the algorithm known as GPS ([10] and
[13]).
Next: Coalition-Resistance
Up: Group Signature Schemes and
Previous: Group Signature Schemes and

