 |

Figures 1 and 2 contain simplified pseudo-code for the algorithm as we've described it. Without loss of generality, we assume that the sequence space for the TCP connection starts at 0, each data packet contains a single byte (and therefore consumes a single sequence number), and data packets are sent according to a periodic distribution. When the algorithm completes, we can calculate the packet loss rate in each direction as follows:
Lossfwd = 1 - (dataReceived/dataSent)
Lossrev = 1 - (ackReceived/ackSent)
 |
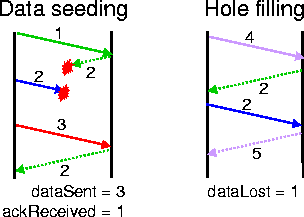
Figure 3 illustrates a simple example. Here, the first data packet is received, but its acknowledgment is lost. Subsequently, the second data packet is lost. When the third data packet is successfully received, the target responds with an acknowledgment indicating that it is still waiting to receive packet number two. At the end of the data seeding phase, we know that we've sent three data packets and received one acknowledgment.
In the hole filling phase, we send a fourth packet and receive an acknowledgment indicating that the second packet was lost. We record the loss and then retransmit the missing packet. The subsequent acknowledgment for our fourth packet indicates that the other two data packets were successfully received.
![]()
![]()