Group Constraint or Surplus

GroupAdjust adjusts a set of candidate allotment vectors to consume a specified amount of memory and/or storage resource. GroupAdjust may adapt the vectors to conform to resource constraints or to allocate a resource surplus to meet system-wide goals.

For example, GroupAdjust can reprovision available memory to maximize hit ratio across a group of hosted services. This is an effective way to allocate surplus memory to optimize global response time, to degrade service fairly when faced with a memory constraint, or to reduce storage loads in order to adapt to a storage constraint. Note that invoking GroupAdjust to adapt to constraints on specific shared storage units is an instance of storage-aware caching [16], achieved naturally as a side effect of model-based resource provisioning.

  

Figure: Using Candidate and GroupAdjust to allocate memory to competing services; in this example, the services are identical except for differing SLA response time targets. Candidate determines the minimum memory to meet each service's target; GroupAdjust allocates any surplus to the services with the least memory.

GroupAdjust assigns available memory to maximize hit ratio across a group as follows. First, multiply Equation (1) for each service by its expected request arrival rate $\lambda$. This gives a weighted value of service hit rates (hits or bytes per unit of time) for each service, as a function of its memory allotment M. The derivative of this function gives the marginal benefit for allocating a unit of memory to each service at its current allotment M. A closed form solution is readily available, since Equation (1) was obtained by integrating over the Zipf probability distribution (see Section 3.1). GroupAdjust uses a gradient-climbing approach (based on the Muse MSRP algorithm [12]) to assign each unit of memory to the service with the highest marginal benefit at its current M. This algorithm is efficient: it runs in time proportional to the product of the number of candidate vectors to adjust and the number of memory units to allocate.

  

Figure: Allotments $[M, \phi ]$ for three competing services in a multiple step experiment. For each step, the graphs represent the allotment percentage of each resource received by each service.

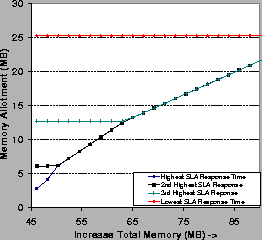
To illustrate, Figure 6 shows the memory allotments of GroupAdjust to four competing services with different cache behavior profiles $(\alpha, S, T)$, as available memory increases on the x-axis. The left-hand graph varies the $\alpha$ and T parameters, holding offered load $\lambda$ constant across all services. Services with higher $\alpha$ concentrate more of their references on the most popular objects, improving cache effectiveness for small M, while services with lower T can cache a larger share of their objects with a given M. The graph shows that for services with the same $\alpha$ values, GroupAdjust prefers to allocate memory to services with lower T. In the low-memory cases, it prefers higher-locality services (higher $\alpha$); as total memory increases and the most popular objects of higher $\alpha$ services fit in cache, the highest marginal benefit for added memory moves to lower $\alpha$ services. These properties of Web service cache behavior result in the crossover points for services with differing $\alpha$ values.

The right-hand graph in Figure 6 shows four services with equal $\alpha$ and T but varying offered load $\lambda$. Higher $\lambda$increases the marginal benefit of adding memory for a service, because a larger share of requests go to that service's objects. GroupAdjust effectively balances these competing demands. When the goal is to maximize global hit ratio, as in this example, a global perfect-LFU policy in the Web servers would ultimately yield the same M shares devoted to each service. Our model-based partitioning scheme produces the same result as the reactive policy (if the models are accurate), but it also accommodates other system goals in a unified way. For example, GroupAdjust can use the models to optimize for global response time in a storage-aware fashion; it determines the marginal benefit in response time for each service as a function of its M, factoring in the reduced load on shared storage. Similarly, it can account for service priority by optimizing for ``utility'' [12,21] or ``yield'' [32], composing the response time function for each service with a yield function specifying the value for each level of service quality.