
To avoid searching a complex space of resource combinations
to achieve a given performance goal, Candidate
follows a simple principle: build a balanced system.
The allocator configures CPU and storage throughput (![]() )
allotments around
a predetermined average utilization level
)
allotments around
a predetermined average utilization level
![]() .
The
.
The
![]() may be set in a ``sweet spot'' range
from 50-80% that balances efficient use of
storage and CPU resources against queuing delays incurred at
servers and storage units.
The value for
may be set in a ``sweet spot'' range
from 50-80% that balances efficient use of
storage and CPU resources against queuing delays incurred at
servers and storage units.
The value for
![]() is
a separate policy choice. Lower values for
is
a separate policy choice. Lower values for
![]() provide more
``headroom'' to absorb transient load bursts for the service, reducing the
probability of violating SLA targets. The algorithm generalizes
to independent
provide more
``headroom'' to absorb transient load bursts for the service, reducing the
probability of violating SLA targets. The algorithm generalizes
to independent
![]() values for each
(service, resource)pair.
,
values for each
(service, resource)pair.
,
The Candidate algorithm consists of the following steps:
| (6) |
 |
Note that the candidate M is the minimum
required to meet the response time target. Given reasonable
targets, Candidate leaves memory
undercommitted. To illustrate,
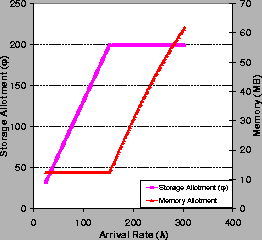
Figure 5 shows
candidate storage and memory allotments ![]() for an example service
as offered Web load
for an example service
as offered Web load ![]() increases along the x-axis. Candidate responds to
increasing load by increasing
increases along the x-axis. Candidate responds to
increasing load by increasing ![]() rather than M.
This is because increasing
rather than M.
This is because increasing ![]() does not require a higher
hit ratio H to meet a fixed response time target.
For a fixed M and corresponding H,
does not require a higher
hit ratio H to meet a fixed response time target.
For a fixed M and corresponding H, ![]() grows
linearly with
grows
linearly with ![]() ,
and so the storage allotment
,
and so the storage allotment
![]() also grows linearly following
also grows linearly following
![]() .
.
Figure 5 also shows how the provisioning scheme adjusts
the vectors to conform to a resource constraint. This example constrains
![]() to 200 IOPS, ultimately
forcing the system to meet its targets by increasing
the candidate M. Candidate
itself does not consider resource constraints;
the next two primitives adapt allotment
vectors on a local or group basis
to conform to resource constraints, or to
allocate surplus resources to improve
performance according to system-wide metrics.
to 200 IOPS, ultimately
forcing the system to meet its targets by increasing
the candidate M. Candidate
itself does not consider resource constraints;
the next two primitives adapt allotment
vectors on a local or group basis
to conform to resource constraints, or to
allocate surplus resources to improve
performance according to system-wide metrics.
 |