 |

The task of our adaptation mechanism is to decide whether doing this is preferable to keeping 100 pages in uncompressed form and zero in compressed form. (We generally assume that pages are compressed before being evicted to disk, whether or not the compression cache is of significant size. Our experiments show that this cost is very small.)
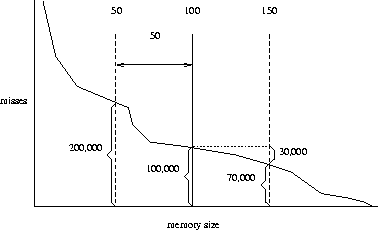
Figure 1 shows an example miss rate histogram decorated with some significant data points. (This is not real data, and not to scale because the actual curve is typically very high on the far left, but the data points chosen are reasonable).
The benefit of this 50/50 configuration is the reduction in disk faults in going from a memory of size 100 to a memory of size 150. We can measure this benefit simply by counting the number of times we fault on pages that are between the 101st and 150th positions in the LRU ordering (30,000 in Figure 1), and multiplying that count by the cost of disk service.
The cost of this 50/50 configuration is the cost of compressing and decompressing all pages outside the uncompressed cache region. These are exactly the touches to the pages beyond the 51st position in the LRU ordering (200,000 touches). Thus, in the example of Figure 1, compressed caching is beneficial if compressing and decompressing 200,000 pages is faster than fetching 30,000 pages from disk.
In general, our recency information allows us to estimate the cost and benefit of a compression cache of a given size, regardless of what the current size of the compression cache actually is, and which pages are currently in memory. That is, we can do a ``what if analysis'' to find out if the current split of memory between caches is a good one, and what might be a better one. We can simply count the number of touches to pages in different regions of the LRU ordering, and interpret those as hits or misses relative to different sizes of uncompressed cache and corresponding sizes of compressed cache and overall effective memory size.