Normalized Benefits and the Effect of Compression Algorithms

Our first goal is to quantify the benefits obtained by using compressed caching and to identify the effect of different compression algorithms on the overall system performance. It is hard to see this effect in Figure 3, which seems to indicate that all compression algorithms obtain similar results.

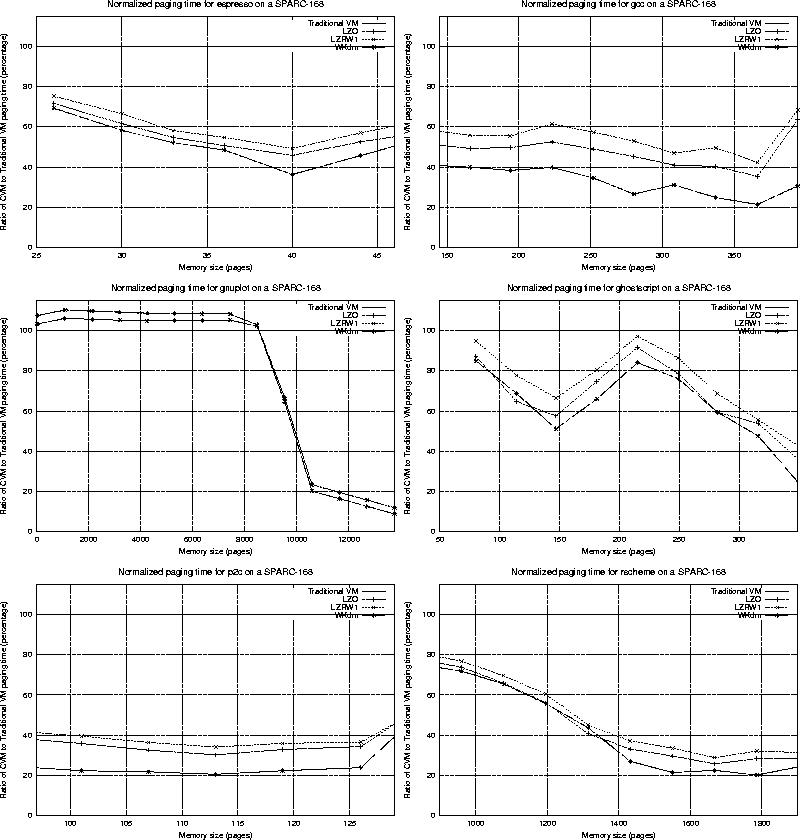
A more detailed plot reveals significant variations between algorithm performance. Figure 4 plots the normalized paging times for different algorithms in the interesting region. (Recall that this usually begins at the size where a program spends 90% of its time paging and 10% of its time executing on the CPU, and ends at a size where the program causes very little paging). By ``normalized paging time'' we mean the ratio of paging time for compressed caching over the paging time for a regular LRU replacement policy.

  

Figure 4: Varying compression algorithms can affect performance significantly. Even though all algorithms yield benefits compared to uncompressed virtual memory, some are significantly better than others.

As can be seen, all algorithms obtain significant benefit over uncompressed virtual memory for the interesting ranges of memory sizes. Benefits of over 40% are common for large parts of the plots in Figure 4. At the same time, losses are rare (only exhibited for gnuplot) and small. Additionally, losses diminish for faster compression algorithms (and faster processors, which is not shown in this plot). That is, when our adaptivity does not perform optimally, its cost can be reduced by having a fast compression algorithm, since it is a direct function of performing unnecessary compressions and decompressions.

Gnuplot is an interesting program to study more closely. The program stores data that are highly compressible (exhibiting a ratio of over 4:1 on average). This way, the compressed VM policy can look at quite large memory sizes, expecting that it can compress enough pages so that all the required data remains in memory. Nevertheless, gnuplot's running time is dominated by a large loop iterating only twice on a lot of data. Hence, for small memory sizes the behavior that the compressed caching policy tries to exploit ends before any benefits can be seen. For larger sizes, the benefit can be substantial, reaching over 80%.

As shown in Figure 4, the performance difference of compressed caching under different compression algorithms can often be over 15%. Our WKdm algorithm achieves the best performance for the vast majority of data points, due to its speed and comparable compression rates to LZO. The LZRW1 algorithm, used by Douglis yields consistently the worst results. This fact, combined with the slow machine used (for current standards) are at least partially responsible for the rather disappointing results that Douglis observed.