 |

We compared the efficiency of the original Refresh algorithm with several other algorithms used for HTTP resource replica selection in [35]. We simulated replicated resources by measuring the latencies of HTTP requests sent for resources residing on 5 or 50 most popular servers in a client trace we collected at Northwestern University. In summary, we found that the Refresh algorithm improved the HTTP request latency compared with the other algorithms described in the literature on average by 55%. The Refresh algorithm improved latency on average by 69% compared with a system using only a single server (i.e. no resource replication). More details on the experimental evaluation can be found in [35].
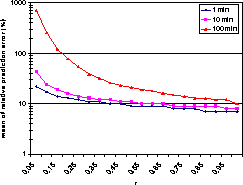
Rather than repeating the experiments from [35], we concentrate here on the accuracy of the estimates used by the above described extension of the Refresh algorithm. The experiments also reveal surprising characteristics of the behavior of HTTP request latency4. In the first experiment, we compare the accuracy of HTTP request latency prediction based on an average calculated using the recursive formula (2). To collect the performance data for the comparison, we measured the HTTP request latencies of the fifty most popular servers outside of Northwestern University campus that were referenced in client traces from [35]. Each server was polled with a 1 minute period5 from a single client at Northwestern University for a period of approximately three days. All together, we collected 228,194 samples of HTTP request latencies. At each step of the experiment, we estimated the next latency sample using the recursive formula (2). The estimate depends on a factor r that determines the weight given to the most recent sample. Figure 5 shows the mean of relative prediction error for various values of r. First, the results show that the HTTP request latency can be predicted relatively accurately from its past samples. For example, even when the sampling interval is increased from 1 minute to 10 and 100 minutes, the mean of relative prediction error is relatively low as shown in Figure 5. Second, the experiment also shows that the smaller the weight given to older samples, the better the accuracy of prediction. Such a behavior can be partly explained by existence of ``peaks'' on the HTTP request latency curve. The larger the value of r, the faster can the average estimate ``forget'' the value of the ``peak''. However, even after filtering out the peaks (all values 5 or 3 times the magnitude of average), we still observed qualitatively similar behavior to that shown in Figure 5. Consequently, we conjecture that the ``memoryless'' behavior is an intrinsic property of the distribution of HTTP request latency (and response time). Finally, we also verified that the accuracy of HTTP request latency prediction based on the recursive formula (5) is as good as the accuracy of prediction based on sliding window used in [35] that lead to a higher storage space overhead.
The feasibility of our approach for latency estimate refreshment depends on the stability of HTTP request latency. If the latency is unstable, then a small value of TTL must be selected to keep the estimates reasonably close to their current values. Consequently, a large number of extra requests is sent only to keep the latency table up-to-date. Therefore, we used the experimental data described above to evaluate the stability of HTTP request latency and gain an insight to selection of the TTL parameter. For each HTTP request latency sample s0, we define a (p,q)-stable period as the maximal number of samples immediately following s0 such that at least p% of samples are within a relative error of q% of the value of s0(this property must hold also for all prefixes of the interval). The stability of a HTTP request latency series can be characterized by the mean length of (p,q)-stable periods over all the samples. Figure 6 shows the means of length of (p,q)-stable periods for various settings of parameters p and q. The results indicate that the HTTP request latency is relative stable. For example, the mean length of the (90,10)-stable period is 41 minutes and the mean length of the (90,30)-stable period is 483 minutes.