The main idea explored in this paper is that of performing user replacement in modem pools. The general problem we are addressing, however, is that of predicting future idle times for user connections to the Internet. Thus, our mechanisms could find application in other domains. A prominent opportunity appears in the case of proactive user disconnections. This is the problem studied by Douglis and Killian [DK99]. Their adaptive timeout technique aims at reducing the total connect time across users. Proactive disconnects are interesting when either the service provider or the user is charged more for longer connection times. (As Douglis and Killian admit, ``Examples of this in the general ISP market are rare, but some services that function effectively as ISPs do observe this property.'') The tradeoffs involved in such a setting are interesting. For instance, there may be a connection initiation fee for users, so a disconnection should be performed only if the charge of staying connected is higher than the charge of connecting anew.
The formulation of the proactive disconnection problem is similar to
that of the replacement problem. There are two thresholds, 
and
. is the minimum idle time before a user is eligible for
disconnection. is the minimum user inactivity time after an
automatic disconnection, for the disconnection to be considered
successful. (``Successful'' may mean cost-effective, psychologically
acceptable, or both.)
It is interesting to consider a proactive disconnection algorithm
based on the same predictions of future idle time as those made by our
replacement algorithms. We have implemented an algorithm called
CIRG-proactive that uses the same information as the CIRG
replacement policy to estimate the future idle time for every user and
disconnects any user with an expected future idle time that is longer
than . For instance, assume a value of 5 minutes for , and a
user who has been idle for 6 minutes and has an idle list:
2, 5, 13, ...
(these values in minutes). The user will be disconnected, since her
expected future idle time is 7 (for a total idle time of 13).
We have performed experiments with CIRG-proactive and compared it to the Douglis and Killian technique. We should emphasize that our results are preliminary. The reason is that we have not re-implemented the Douglis and Killian mechanism. Hence, we could not examine its effects on our long traces (the Telesys traces). Instead, we use the measurements already computed by Douglis and Killian for the AT&T Labs trace and compare them to the performance of CIRG-proactive.
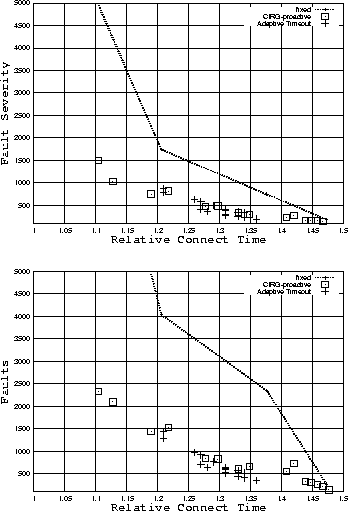
Figure 7: Fault severity and absolute number of faults
vs. relative connect time for three policies: a fixed timeout
policy, CIRG-proactive, and the Douglis and Killian technique
(``adaptive timeout''). Connection times are normalized with
respect to the connection time of an optimal, off-line
policy.
Figure 7 presents the results of our comparison. It
shows two scatter plots: one of fault severities and connection times
and another of absolute fault counts and connection times. Both show
results for a fixed timeout policy, CIRG-proactive, and the Douglis
and Killian technique applied to the AT&T Labs trace, with 15
workaholics excluded. Connection times are normalized with respect to
the connection time of an optimal, off-line (i.e., clairvoyant)
policy. That is, the optimal policy would encounter 0 faults for a
relative connect time of 1. The value of is 5 minutes and the
values of for the fixed timeout policy are 2, 5, 10, and 15
minutes. (These values are chosen to be identical with those used by
Douglis and Killian in their study.) The values of for
CIRG-proactive are all integral minute values from 1 to 15 minutes. 18
data points for the Douglis and Killian technique are plotted, each for a
different combination of adaptivity (multiplicative or additive) and
different parameters. As we are comparing to the approach as a whole,
we do not distinguish between the different flavors of the Douglis and
Killian technique (for this, the reader is referred to
[DK99]).
We can see from Figure 7 that CIRG-proactive performs on
average just as well as the Douglis and Killian policy and they both
perform significantly better than fixed timeouts. Nevertheless, the
values for the Douglis and Killian approach are clustered together in
the connect-time/user-inconvenience space, while CIRG-proactive offers
a wider range of options in the tradeoff between user inconvenience
and total connect time. It is worth noting that CIRG-proactive offers
this wide range of options with only a single parameter that can be
tuned (the minimum idle time for disconnection) while the
Douglis and Killian approach has several degrees of variability
(additive vs. multiplicative adaptivity with two numeric parameters
for each variant). The wide range of CIRG-proactive values means that
we can argue that CIRG-proactive is strictly better than a fixed
timeout policy: For each fixed timeout point in the plot, we can find
a CIRG-proactive point that is below it and to its left. That is, for
each fixed timeout setting, we can find a value of for
CIRG-proactive so that it incurs both a lower fault severity (or fewer
faults) and a lower total connect time. The Douglis and Killian
technique provides no such guarantee for the values shown.