


Next: The Libart Imaging Model
Up: Delayed Update/Redraw Model
Previous: Delayed Update/Redraw Model
We have not explained how the canvas actually figures out the area
that needs to be repainted. Let us consider a few simple cases:
- A solid-colored rectangle with dimensions
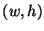 is translated
with offsets
is translated
with offsets 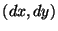 such that
such that 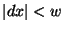 and
and 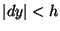 . In this
case, the minimal redraw area consists of two L-shaped regions that
are the symmetric difference between the old and the new rectangles
(see Figure 1).
. In this
case, the minimal redraw area consists of two L-shaped regions that
are the symmetric difference between the old and the new rectangles
(see Figure 1).
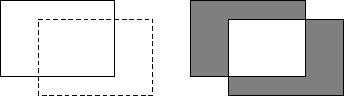
Figure 1:
When a solid-colored rectangle moves, the redraw area
consists of two L-shaped regions.
 |
- A solid-colored rectangle changes color. In this case, the
whole area occupied by the rectangle needs to be redrawn.
- A solid-colored circle changes radius. The minimal redraw area
thus consists of the donut-shaped region which is, again, the
symmetric difference between the old and new circles.
- Some characters in a string of text are changed, for example,
when the user is editing a label. If the string is drawn using a
monospaced font, the minimal redraw area consists of the area occupied
by the characters that changed. If the string is drawn using a
proportional font, the redraw area will be more complicated.
One of the goals of the canvas is to compute the minimal redraw area
for each operation. This is important because we wish to make the
final bitblt operations as small as possible; experiments have shown
that memory bandwidth tends to be a bigger problem than CPU speed.
Canvas items have two important methods, ::update() and
::draw()1. The former is
reponsible for calculating the area that needs to be redrawn when the
item's attributes change, and the latter gets called when the final
redraw area has been computed by the canvas and an item needs to paint
itself.
The full sequence of operations that starts when an item's attributes
are changed and ends when the canvas paints to the screen is as
follows:
- A state change happens in a canvas item, usually from direct
manipulation through the user interface. An item may thus change
attributes like color or position.
- The canvas item stores an iternal flag saying that it needs to
change one of its attributes, and also stores the necessary
information to change that attribute. For example, an item may store
``I need to change my fill color to blue'', or ``my radius changed to
7.5 units''.
- The canvas item then queues an update from the canvas using the
gnome_canvas_item_request_update() function. The canvas
installs an idle handler on the GTK+ main loop.
- The application keeps running, possibly requesting attribute
changes from other items, until it finishes its work and all its
interaction-related tasks, and gets back to the idle loop.
- The idle handler for the canvas is run. The canvas calls the
::update() method of each item that requested an update.
- The ::update() method for an item flags the item as no
longer needing an update. It should recalculate the item's internal
state based on the flags set in step 2, for example, by changing
colors or line styles in an X graphics context (GC). This method is
also responsible for recomputing the item's bounding box if the item's
bounds changed. Then, it should queue a redraw from the canvas based
on its new state. We will later describe how this area is
represented.
- After all items that need it have been updated, and as such they
have recomputed their bounding boxes and queued the appropriate
redraws, the canvas calls the ::draw() or ::render()
method of items that need it. This method is passed a temporary
pixmap in the case of a canvas in GDK mode, or an RGB pixel buffer
in the case of an antialiased canvas.
- The canvas is now fully updated and redrawn, and the application
continues to run.
As we have seen, the ::update() method is responsible for doing
housekeeping work like changing GC colors and line styles, recomputing
an item's bounding box, and queueing the proper redraws. This method
is called from the canvas' idle handler. The reason for delaying GC
updates and the like to the idle loop is that an application may
change many attributes of a canvas item before getting back to the
idle loop; if the item changed GCs or recomputed its bounding box for
every time an attribute was changed, this could turn into a
performance problem, since many such operations are expensive.
Delaying all the updating work until the idle loop means that the
application's interaction with items has finished, so the items know
their final state at that point and can compute the most efficient way
to do their respective updates.


Next: The Libart Imaging Model
Up: Delayed Update/Redraw Model
Previous: Delayed Update/Redraw Model
Federico Mena Quintero
2000-05-08
