|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
USENIX 2002 Annual Technical Conference Paper
[USENIX 2002 Technical Program Index]
Maximizing Throughput in Replicated Disk Striping of Variable Bit-Rate Streams
AbstractIn a system offering on-demand real-time streaming of media files, data striping across an array of disks can improve load balancing, allowing higher disk utilization and increased system throughput. However, it can also cause complete service disruption in the case of a disk failure. Reliability can be improved by adding data redundancy and reserving extra disk bandwidth during normal operation. In this paper, we are interested in providing fault-tolerance for media servers that support variable bit-rate encoding formats. Higher compression efficiency with respect to constant bit-rate encoding can significantly reduce per-user resource requirements, at the cost of increased resource management complexity. For the first time, the interaction between storage system fault-tolerance and variable bit-rate streaming with deterministic QoS guarantees is investigated. We implement into a prototype server and experimentally evaluate, using detailed simulated disk models, alternative data replication techniques and disk bandwidth reservation schemes. We show that with the minimum reservation scheme introduced here, single disk failures can be tolerated at a cost of less than 20% reduced throughput during normal operation, even for a disk array of moderate size. We also examine the benefit from load balancing techniques proposed for traditional storage systems and find only limited improvement in the measured throughput.IntroductionStriping media files across multiple disks has the advantage of keeping the disks implicitly load-balanced. With several concurrent sessions of playback asynchronously started, different parts of each file are accessed from different disks. As a result it is no longer necessary to replicate media files according to their popularity, which leads to lower resource requirements and system administration cost. The disadvantage of disk striping is decreased system reliability because media files are left partially inaccessible when one or more disks fail. This causes service disruption to all the users served by the disk array at the moment of the failure. In contrast, when an entire file is stored on a single disk, only those users accessing files on the failed disk are negatively affected.Previous work has addressed the general problem of disk array reliability by using data redundancy techniques to allow recovery of inaccessible data [12]. Some of these techniques have been successfully extended for handling the case of striped media files as well [6,25]. However, all the known analytical and experimental work on this subject is either limited to streams of constant bit rates (CBR), or assumes stochastic admission control [27,29]. Variable bit-rate (VBR) encoding of video can considerably reduce the size of the generated media files when compared to constant bit-rate encoding of equivalent perceptual quality [18,22]. In addition, knowledge about the resource requirements of stored streams during transmission can be leveraged for better predicting access delays, and offering deterministic QoS guarantees [11]. Although striping of VBR streams has been previously studied, it remains unclear whether increased reliability can be provided with deterministic QoS guarantees in cost-effective ways. Variability in the resource requirements over time makes efficient disk space allocation combined with access delay predictability a challenging task. Data striping across multiple disks with sufficient redundancy to tolerate failures further aggravates the problem due to the need for keeping balanced the storage space and bandwidth requirements across the disk array, under both normal-operation and failed-disk conditions. In the present paper, we describe a number of data redundancy and bandwidth reservation schemes that can tolerate single disk failures without service interruption. We experimentally evaluate the cost of increased reliability in terms of reduced throughput during the normal operation of the system using a video server prototype implementation and MPEG-2 streams. We also investigate the achieved disk bandwidth utilization during normal and failed-disk operation. Additionally, we examine the extra benefit from retrieving data replicas stored on the least loaded disks, and from fragmenting data replicas across multiple disks. The rest of this paper is organized as follows. In Section 2, we describe basic assumptions and architectural decisions of our system. In Sections 3, 4 and 5, we introduce alternative policies for replicating stream data and reserving disk bandwidth for improved reliability. In Section 6, we briefly present our prototype implementation and the experimentation environment that we use. In Section 7, we compare the performance of different replication techniques under alternative bandwidth reservation schemes and load balancing enhancements. In Section 8, we discuss possible improvements and extensions, and in Section 9 we summarize our conclusions. System ArchitectureIn the present section, we describe the system architecture along with important resource management and reservation techniques that we use [2].OverviewThe operation of our media server is typical in current system designs. Client devices submit playback requests concurrently to the server. The system is assumed to operate according to the server-push model. When a playback session starts, the server periodically sends data to the client until either the end of the stream is reached, or the client explicitly requests suspension of the playback. Data transfers occur in rounds of fixed duration Tround. In each round, an appropriate amount of data is retrieved from the disks into a set of server buffers reserved for each active client. Concurrently, data are sent from the server buffers to the client through the network interfaces (Figure 1). The amount of stream data periodically sent to the client is determined by the decoding frame rate of the stream, the buffering constraints of the receiver, and the resource management policy of the network. As a minimum requirement, the client should receive in each round the amount of data that will be needed by the decoder during the next round.
The streams are compressed according to any encoding scheme that supports constant quality quantization parameters and variable bit rates. Playback requests arriving from the clients are initially directed to an admission control module, where it is determined whether enough resources exist to activate the requested playback session either immediately or within a limited number of rounds. A schedule database maintains for each stream information on how much data needs to be accessed from each disk in any given round, the amount of server buffer space required, and how much data needs to be transferred to the client. This scheduling information is generated when the media stream is first stored, and is used for both admission control and transfer of data during playback. Stride-Based Disk Space AllocationIn our experiments, we use a method called stride-based allocation for allocating disk space [3]. In stride-based allocation, disk space is allocated in large, fixed-sized chunks called strides. The strides are chosen larger than the maximum stream request size per disk during a round. This size is known a priori, since stored streams are accessed sequentially according to a predefined (generally variable) rate. A stride may contain data of more than one round. When a stream is retrieved, only the requested amount of data is fetched to memory during a round, and not the entire stride.Stride-based allocation eliminates external fragmentation due to the fixed-size strides. Internal fragmentation remains negligible because of the large size of the streams relative to strides. Another advantage of stride-based allocation is that it sets an upper-bound on the estimated disk access overhead during retrieval. Since the size of a stream request never exceeds the stride size during a round, at most two partial stride accesses will be required to serve the request of a round on each disk.
A mathematical abstraction of the resource requirements is necessary for
scheduling streams. We consider a system with D functionally equivalent
disks. Data of each stream are stored as sequences of strides on each disk.
Each stride comprises an integer number of consecutive logical blocks with
fixed size Bl. The logical block size is a multiple of
the physical sector size Bp of the disk. Both the disk
transfer requests and the memory buffer reservations are specified in multiples
of the block size Bl. The Disk Striping SequenceSd
of length Ld determines the amount of data
Sd(i,k), | |||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
In previous work, we have demonstrated that variable-grain striping
of media files leads to equally utilized disks under sequential playback
workloads [2]. Although mirroring has previously
been only used with data striped using fixed-size blocks, in principle
it could be applied to variable-grain striping as well. During sequential
playback of a media file with no failed disks, each disk is accessed every
D
rounds, where D is the total number of disks. In order to preserve
the load-balancing property when a disk fails, data of a media file stored
consecutively on each disk could be replicated round-robin across the remaining
disks (or a subset of them). The unit of replication corresponds to data
retrieved by a client during one round of playback.We call this mirroring
approach
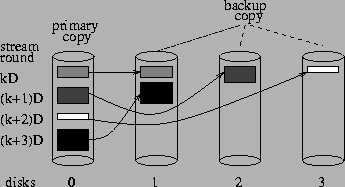
Deterministic Replica Placement. In Figure 2,
for example, disk 0 is shown to store stream data requested during rounds![]() ,
, ![]() ,
, ![]() and
and ![]() .
The respective replicas are distributed round-robin among disks 1, 2 and
3.
.
The respective replicas are distributed round-robin among disks 1, 2 and
3.
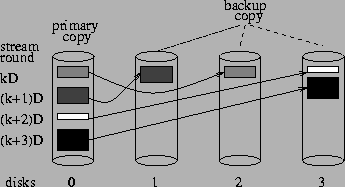 |
Intuitively, having replicas of one disk's primary data distributed round-robin across the rest of the disks can keep the surviving disks equally utilized when one disk fails. An alternative replication approach would use some pseudo-random sequence for specifying the disks that store the backup copies of one disk's primary data. An obvious constraint is that primary and backup copies are stored on different devices. The unit of replication corresponds to the data of a media file requested by a client in one round of playback. We call this mirroring technique Random Replica Placement.
An example is shown in Figure 3, where backup
copies of data requested in rounds ![]() are randomly placed on disks 1 to 3. It has been previously suggested that
random placement of primary and backup replicas across different disks
is applicable to a wider range of workload types and can outperform striping
policies with round-robin placement [27]. In
a later section, we examine this argument in the particular case of variable
bit-rate streams by comparing it against deterministic replica placement.
are randomly placed on disks 1 to 3. It has been previously suggested that
random placement of primary and backup replicas across different disks
is applicable to a wider range of workload types and can outperform striping
policies with round-robin placement [27]. In
a later section, we examine this argument in the particular case of variable
bit-rate streams by comparing it against deterministic replica placement.
The net benefit from uninterrupted service during disk failures is equal
to the difference between two measures. One is the cost of having users
frustrated due to interrupted service from a failed disk. Its quantification
would require determining the minimum number of users negatively affected
when a disk fails. Detailed study of this issue is left for future work.
The other measure is the cost of rejecting user requests due to additionally
reserved disk bandwidth during normal operation. In the rest of this paper,
we describe alternative approaches for reserving disk bandwidth (or equivalently
access time) and improving reliability in media servers that support variable
bit-rate streams. Subsequently, we experimentally evaluate the actual cost
of these approaches in terms of reduced system throughput during normal
system operation.
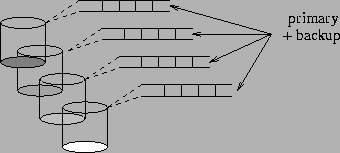 |
In what we call Mirroring Reservation, disk bandwidth is reserved
for both the primary and backup replicas of a media file during its playback
(Figure 4). At first glance, this seems to
be a reasonable approach for guaranteeing timely access to backup replicas
during a single disk failure. However, when compared to the non-redundant
case, it doubles the bandwidth requirements of each stream and halves the
maximum system throughput, assuming disk bandwidth is the bottleneck resource
in the system. Indeed, we would prefer that the load normally handled by
a failed disk is equally divided among the D-1 surviving disks.
Thus, tolerating one disk failure should require that the extra bandwidth
reserved on each disk be equal to ![]() its bandwidth capacity. Instead, mirroring reservation reserves extra bandwidth
on each disk equal to half its bandwidth capacity.
its bandwidth capacity. Instead, mirroring reservation reserves extra bandwidth
on each disk equal to half its bandwidth capacity.
Essentially, it is wasteful to reserve on a disk extra bandwidth for accessing backup replicas of primary data stored on more than one other disk. When a disk fails, we only need an estimate of the additional access load incurred on every surviving disk. In order to know that, the access time of the backup replicas stored on one disk can be accumulated separately for every disk that stores the corresponding primary data. Then, the additional access time that has to be reserved on a disk in each round is equal to the maximum time required for retrieving backup replicas for another disk that has failed. The maximum across every other disk is reserved, since we don't know in advance which other disk is going to fail.
For each disk, our implementation maintains D vectors, indexed
by round number of system operation. One of the vectors keeps track of
the total access time required for retrieving primary data. The remaining
D-1
vectors keep track of access delays due to backup data corresponding to
primary data of the remaining disks. For every disk, we reserve the sum
of the primary data access time and the maximum of the backup data access
times required in each round. We refer to this more efficient scheme as
Minimum
Reservation. An example with four disks is illustrated in Figure 5.
In a later section, we discuss ways for limiting the additional computational
and memory requirements of this approach.
|
||||||||||||
The two disk bandwidth reservation schemes that we just described can
be orthogonally combined with the two replica placement policies that we
introduced previously, as it is shown in Table 1.
The backup replica blocks corresponding to the primary data of each disk are distributed either round-robin or pseudo-randomly across the rest of the disks, depending on whether deterministic or random replica placement is used. In the case of random replica placement, we improve block distribution by avoiding reusing the same disk for storing multiple replica blocks of the same file in one round unless we are running out of disks. When multiple blocks of size Bd are retrieved from a disk during one round of a file playback, the minimum required number of read requests is submitted to the disk, instead of one per block.
Alternatively, during normal operation we could take advantage of multiple available data replicas by dynamically deciding to retrieve the replica stored on the disk expected to be the least loaded. The disk choice could be based on access time estimations available through resource reservations that are made during admission control. We use the term Dynamic Balancing for this technique. It can be fully applied when all the disks are functional and is expected to reduce the load of the most heavily utilized disks in each round.
Both these two techniques have previously been found to improve performance when applied to traditional transaction processing workloads [23]. Replica declustering has also been tried with constant bit-rate stream playback [9,15]. Due to the potential for load imbalance and reduced device utilization introduced by variable bit-rate streams, we investigate the benefit from load-balancing techniques in that context.
The basic responsibilities of the media server include file naming, resource reservation, admission control, logical to physical metadata mapping, buffer management, and disk and network transfer scheduling.
With appropriate configuration parameters, the system can operate at
different levels of detail. In Admission Control mode, the system
receives playback requests, does admission control and resource reservation,
but no actual data transfers take place. In
Simulated Disk mode,
most modules become functional and disk request processing is simulated
using the specified DiskSim disk array. Techniques for file system simulation
similar to those previously proposed are used for integrating the simulated
disks with our media server prototype [31].
There is also the
Full Operation mode, where the system accesses
hardware disks and transfers data to fixed client network addresses. For
the experiments in the current study, we used both the Admission Control
and the Simulated Disk Mode.
 |
(1) |
For each playback request that arrives, the admission control module
checks whether available resources exist for every round during playback.
The test considers the data transfer requirements of the requested playback
for every round and also the corresponding available disk transfer time,
network transfer time and buffer space in the system. If the request cannot
be initiated in the next round, the test is repeated for each round up
to ![]() rounds
into the future, until the first round is found where the requested playback
can be started with guaranteed sufficiency of resources. Checking
rounds
into the future, until the first round is found where the requested playback
can be started with guaranteed sufficiency of resources. Checking ![]() rounds into the future achieves most of the potential system capacity as
was shown previously [2]. If not accepted,
the request is rejected rather than being kept in a queue.
rounds into the future achieves most of the potential system capacity as
was shown previously [2]. If not accepted,
the request is rejected rather than being kept in a queue.
We used six different VBR MPEG-2 streams of 30 minutes duration each. Every stream has 54,000 frames with a resolution of 720x480 and 24 bit color depth, 30 frames per second frequency, and a IB2PB2PB2PB2PB2 15 frame Group of Pictures structure. The encoding hardware that we use generates bit rates between 1 Mbit/s and 9.6 Mbit/s. The statistical characteristics of the clips are given in Table 2. The coefficients of variation of bytes per round lie between 0.028 and 0.383, depending on the content type. In the mixed benchmark, the six different streams are submitted round-robin. Where appropriate, experimental results from individual stream types are also shown.
|
||||||||||||||||||||||||||
The disks assumed in our experiments are Seagate Cheetah with ultra-wide SCSI interface and the features shown in Table 3. Such disks were state of the art about three years ago, and have all the basic architectural characteristics of today's high-end drives. The logical block size Bl was set to 16 KB bytes, while the physical sector size Bp was equal to 512 bytes. The stride size Bs in the disk space allocation was set to 2 MB. The server memory is organized in buffers of fixed size Bl=16 KB bytes each, with space of 64 MB for every extra disk. The available network bandwidth was assumed to be infinite, leaving contention for the network outside the scope of the current work.
In our experiments, the round time was set equal to one second. We found
this round length to achieve most of the system capacity with tolerable
initiation latency. This choice also facilitates comparison with previous
work in which one second rounds were used. We used a warmup period of 3,000
rounds and calculated the average number of active streams from round 3,000
to round 9,000. The measurements were repeated until the half-length of
the 95% confidence interval was within 5% of the estimated mean value of
the number of active streams. The system load was fixed at ![]() ,
which allows the system to reach its capacity while keeping the playback
startup latency limited [2].
,
which allows the system to reach its capacity while keeping the playback
startup latency limited [2].
We start with a performance comparison between the deterministic and
random replica placement policies under the mirroring reservation scheme.
Subsequently, we examine the improvement to the two placement policies
when minimum reservation is applied. We also investigate the benefit of
dynamic balancing assuming that disk bandwidth in each round is reserved
for only one data replica out of the two available. Finally, we consider
declustering the backup replica of each stream across multiple disks and
allocating bandwidth according to the minimum reservation scheme.
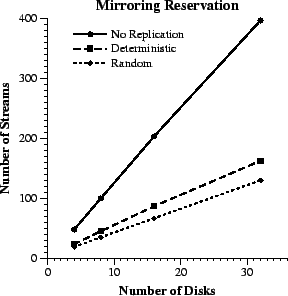 |
From measurements that we did (not shown here), we found that about half of the average disk time reserved in the replicated case is wasted for the possibility that the backup data will be retrieved. Furthermore, the access time reserved on each disk by random replica placement is about 15%-25% less than that of deterministic placement. Pseudo random choice of the disk that stores a backup replica does not completely eliminate the possibility of one disk storing more replicas than another, especially with small disk arrays. The probability of that occurring drops as the size of the disk array increases, though. However, deterministic placement is more consistent in fairly distributing the access load across the disk array devices.
When a disk fails, about 25-30% of the reserved disk bandwidth remains unused under both placement policies. This is not surprising, since the mirroring reservation scheme allocates disk bandwidth for both the primary and backup replicas of each accepted stream. We see how this inefficiency is alleviated by the minimum reservation scheme in the following subsection.
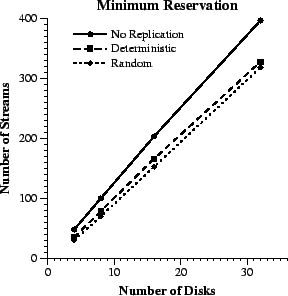 |
Figure 7 compares the throughput of
the different replica placement policies under minimum reservation. At
eight disks, the number of streams supported by deterministic placement
is only 21% lower than that with no replication. This difference becomes
18% and 17%, respectively, with sixteen and thirty two disks. From the
way that the disk bandwidth is allocated in the minimum reservation scheme,
we would expect the total bandwidth that remains unutilized during normal
operation to be equal to the bandwidth capacity of one disk. Therefore,
the percentage of unused throughput with respect to the non-replicated
case should be decreasing proportionally with the number of disks in the
system. For example, ideally with 16 disks only the ![]() of the total disk bandwidth should remain unused during normal operation.
of the total disk bandwidth should remain unused during normal operation.
 |
However, in practice, the percentage of the total unused bandwidth of each disk does not change proportionally with the number of disks (Figures 8). This effect can be explained by the MAX() operator that is applied over the estimated time for accessing the backup replicas of different disks, in combination with the relatively large size (more than half megabyte on average) of the data retrieved for a stream in each round. We explore later the potential improvement from declustering backup replicas across multiple disks.
Additionally, the difference between deterministic and random replica placement becomes less significant than the statistical uncertainty at thirty two disks. Not surprisingly, deterministic placement maintains a clear advantage (of about 15%) for smaller disk array sizes due to the more regular way of distributing the backup replica access load across the different devices. These observations are consistent with the average access time reserved on each disk across different stream types and disk array sizes shown in Figure 8.
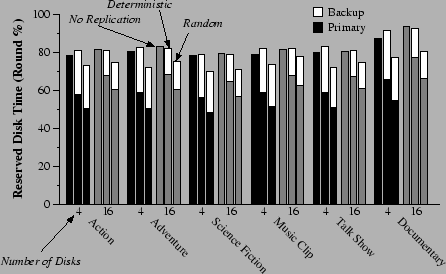
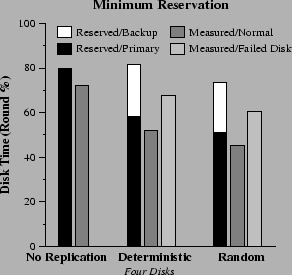 |
In Figure 9, we show the measured disk busy time. Under normal disk operation, we observe that deterministic placement keeps the disks busy an amount of time that is 6% lower than what is reserved for primary data.3 When one disk fails, the remaining disks are busy 14% time less than the total reserved. With random replica placement, the corresponding difference becomes 13% of the round length. This is a significant improvement in comparison to the 25-30% difference between reserved and measured time that we reported for mirroring reservation. We should keep in mind that, with disk array size equal to four, about one third of each disk's bandwidth has to be reserved for the case that one disk fails, and this fraction drops as the disk array size increases to sixteen (Figure 8).
It is interesting that, when the reserved backup access time is put into use due to a disk failure, the difference between reserved and utilized access time increases from 6-8% to 13-14%. At first glance this discrepancy appears as reduced accuracy in access time estimation. In fact it is due to the MAX() operator that we apply to the backup access times corresponding to different disks in each round. This reserves enough access time to ensure uninterrupted system operation for any particular failed disk. However, the reported measured time is taken when the disk 0 is assumed inaccessible (Figure 2). Overall, we believe that some limited discrepancy between predicted and measured access time leaves a reasonable cushion space for stable operation. This makes the system operation more robust, and guards it against nondeterministic factors, such as the system bus contention due to network transfers, not included in the previous measurements.
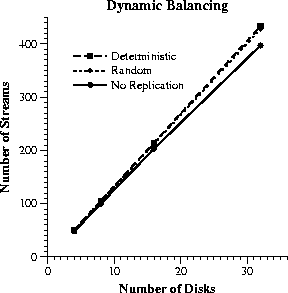
From Figure 10, we see that, when
this load balancing scheme is used, both replica placement policies can
support 5-10% more streams than the non-replicated case. The difference
between the two placement policies is statistically insignificant, however,
since the gain from the dynamic replica access exceeds the improved load
balancing of deterministic placement. Determining during admission control
which disk will be used for each data access is a reasonable policy for
removing hot spots in the disk array. However, under sequential workloads
the different disks are equally utilized already, and only a limited additional
performance benefit can be accrued with the above policy.
 |
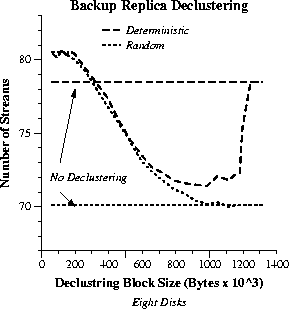
In Figure 11, we consider the case of declustering backup replicas across multiple disks using a fixed block size Bd. This approach is expected to let the failed-disk load be more fairly shared among the surviving disks. With small block sizes, better load balancing leads into some limited throughput improvement. As the block size becomes larger, load balancing gets successively worse and throughput decreases, because declustering creates fragments with sizes increasingly different.
We also anticipate that, with larger block sizes, the number of disks
accessed for each stream drops and the total head movement overhead becomes
lower. On the other hand, our stride-based allocation scheme ensures that
at most two head movements are required per stream on each disk regardless
of how small the block size is. This keeps limited the negative effect
of access overhead to throughput. Finally, we observe a threshold behavior
around ![]() bytes.
This is the maximum amount of data retrieved in one round for each stream
and originates from the bit-rate parameters used during encoding (Table
3).
Effectively, beyond this point there is no declustering.
bytes.
This is the maximum amount of data retrieved in one round for each stream
and originates from the bit-rate parameters used during encoding (Table
3).
Effectively, beyond this point there is no declustering.
 |
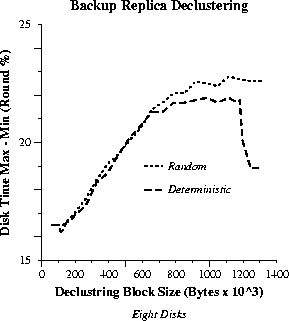 |
These observations are also verified by Figure 12,
that shows the average difference between the access times of the most
and least loaded disk in each round. Since the reserved access time of
the most heavily loaded disk is typically 99% in each round, the plots
in Figure 12 essentially indicate the access
time requirements of the least loaded one. It is remarkable how the shape
of the plots is reflected to those tracking the system throughput in Figure
11.
We conclude that even the least loaded disk is expected to remain more
than 80% utilized under deterministic replica placement with no declustering
(equivalently, with declustering block size larger than ![]() ).
).
In summary, declustering is only worthwhile with small declustering block sizes, and its overall benefit is found to be limited in the media streaming case (less than 3% with eight disks). Moreover, the throughput of random replica placement never exceeds that of deterministic.
The minimum reservation scheme requires maintaining number of vectors equal to the square of the number of disks. Each vector is accessed in a circular fashion and has minimum length equal to that of the longest stream expressed in numbers of rounds. When using large disk arrays, this might raise concerns regarding the computational and memory requirements involved. In practice, the reduction in unused bandwidth is diminishing as the number of disks increases beyond sixteen. Therefore, it makes sense to apply the data replication within disk groups of limited size, when the disk array size becomes larger. This keeps the bookkeeping overhead limited and preserves the scalability of our method when stream data are striped across large disk arrays.
In previous work, we found that striping data using fixed-size blocks achieves lower throughput than when using variable-grain striping [2]. The backup replica declustering should not be confused with fixed-size block striping, since the primary data still use variable-grain striping. This maintains some benefit from multiplexing requests of different transfer sizes in each round, and absorbs correlations that otherwise would create maximum requirements much higher than the average.
Provisioning for VCR functionality is an important issue that we don't consider extensively in the present paper. In general, such flexibility would require deallocation of previously reserved resources, when a stream playback is suspended or stopped earlier than its normal termination. This can done in a straightforward way, when accumulating disk access delays separately for primary and backup data replicas, as was already described above.
The techniques we presented here could be extended in straightforward ways for handling multiple disk failures. That would require storing multiple backup replicas, and making bandwidth reservations for more than one failed disk. In servers consisting of multiple nodes, failure of an entire node can also be handled gracefully, by keeping each disk of a node in a separate disk group and limiting the replication within each group. When a node fails, inaccessible data for each of its disks can be retrieved using replicas available on other disks of the corresponding groups [9,15].
In our previous work, we found the throughput measured with disk striping of variable bit-rate streams to increase linearly as a function of the number of disks [2,1]. We also described several design decisions of our server prototype implementation [3]. The system throughput is further improved when the disk bandwidth requirements of individual streams are smoothed across different playback rounds [4], and high disk bandwidth utilization is achieved across both homogeneous and heterogeneous disks. System reliability is a crucial issue when building infrastructure for commercial services. Addressing this issue creates a strong case for storage of variable bit-rate streams, and makes the results of the present paper indispensable part of our previous published work.
The related work from media server research is mostly focused on fault-tolerance techniques when striping constant bit-rate streams [32,5,6]. Disks are grouped into clusters, and data blocks from separate disks in each cluster are combined with a parity block to form parity groups. The blocks of a parity group are considered to be retrieved and transmitted in one or multiple rounds, and the parity blocks are stored on data disks or dedicated parity disks. For improving overall efficiency, certain data blocks are not transmitted in a transition period following a disk failure.
Ozden et al. propose reading ahead the data blocks of an entire parity group prior to their transmission to the client [25]. When a data block cannot be accessed, it can be reconstructed using a parity block that is read instead. Alternatively, an entire parity group is retrieved each time a block cannot be accessed. Balanced incomplete block designs are used for constructing parity groups that keep the load of the disk array balanced [20,25]. The dynamic reservation scheme that they introduce minimizes the extra bandwidth that has to be reserved on a disk for reconstructing failed-disk data blocks.
Gafsi and Biersack compare several performance measures of alternative data-mirroring and parity-based techniques for tolerating disk and node failures in distributed video servers [15]. When entire data blocks of one disk are replicated on different disks, half of the total bandwidth of each disk is reserved for handling the disk failure case. The wasted throughput is critically reduced with the minimum reservation scheme that we propose here.
Tewari et al. study parity-based redundancy techniques for tolerating disk and node failures in clustered servers [30]. By distributing the parity blocks of an object on a random permutation of certain disks they can keep balanced the system load when a disk fails. Alternatively, Flynn and Tetzlaff replicate data blocks across non-intersecting permutations of disk groups [14]. Multiple available data blocks can be used for dynamic balancing of disk bandwidth utilization across different devices. Instead, Birk examines selectively accessing parity blocks of video streams for better balancing the system load across multiple disks [7].
For failures in video servers supporting variable bit-rate streams, Shenoy and Vin apply lossy data recovery techniques that rely on the inherent redundancy in video streams rather than error-correcting codes. Alternatively, they propose taking advantage of the sequential block accesses during playback and reconstructing missing data from surrounding available blocks, at the cost of an initial playback latency, or temporary disruption when a failure occurs [29].
Bolosky et al. decluster the block replicas of one disk across dother disks. In case of disk failure, the extra bandwidth required for retrieving the data of the failed disk is shared among the d other disks [9]. In later work, they also consider providing fault-tolerant support for multiple streams with different bit rates [10]. In our experience, declustering does not add significant improvement with respect to the case of replicating the data blocks of one disk in their entirety on different disks.
Mourad describes the doubly-striped disk mirroring technique that distributes replica blocks of one disk round-robin across the rest of the disks [24]. The system load is equally distributed across the surviving disks in case of a disk failure. The deterministic replica placement that we describe extends doubly-striped mirroring for handling variable bit-rate streams and the reduced device utilization that they potentially introduce.
Santos et al. compare disk striping against data replication on randomly chosen disks [27]. Using constant bit-rate streams, they conclude that random replication can outperform disk striping with no replication. In our comparison using variable bit-rate streams instead, we found an advantage of deterministic replication over random replication that diminishes as the number of disks increases.
|
This paper was originally published in the
Proceedings of the 2002 USENIX Annual Technical Conference, June 10-15, 2002, Monterey Conference Center, Monterey, California, USA.
Last changed: 16 May 2002 ml |
|