



Next: User Behavior Analysis
Up: Notification Log Analysis
Previous: Notification Message Size and
Message Popularity Analysis and Its Implications
Several studies have
found that web accesses follow Zipf-like distribution: the number of requests
to the ith most popular object is proportional to
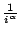 [3,4,6,7,10,14,16].
The estimates of
[3,4,6,7,10,14,16].
The estimates of 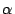 range from 0.5 to 1 for web
proxy logs [7,10,14], and range from 1 to 2 for web server
logs [4,16]. It is interesting to examine whether notification
messages exhibit a similar property.
To do the above, we take the following approach: For each notification document,
we count the number of notification messages (i.e., copies) that were sent on a given
day. We plot the total number of transmissions of a document (i.e.,
notification messages) versus the popularity ranking of the document on a
log-log scale. Figure 5 shows the plot for August 21,
2000. The plots for the other days are similar, and are omitted for
brevity. If we ignore the first few notification documents and the flat tail
in Figure 5 (as is done in the previous
work [6,7,16]), we note that the curve fits a straight line
reasonably well. We compute the values of
range from 0.5 to 1 for web
proxy logs [7,10,14], and range from 1 to 2 for web server
logs [4,16]. It is interesting to examine whether notification
messages exhibit a similar property.
To do the above, we take the following approach: For each notification document,
we count the number of notification messages (i.e., copies) that were sent on a given
day. We plot the total number of transmissions of a document (i.e.,
notification messages) versus the popularity ranking of the document on a
log-log scale. Figure 5 shows the plot for August 21,
2000. The plots for the other days are similar, and are omitted for
brevity. If we ignore the first few notification documents and the flat tail
in Figure 5 (as is done in the previous
work [6,7,16]), we note that the curve fits a straight line
reasonably well. We compute the values of 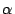 using least-square fitting,
after excluding the top 20 documents and the flat tail (the latter set
represents the notification documents that were sent only once or twice). The
straight line on the log-log scale implies that the notification documents
follow a Zipf-like distribution. We find that for our complete data-set the
value of
using least-square fitting,
after excluding the top 20 documents and the flat tail (the latter set
represents the notification documents that were sent only once or twice). The
straight line on the log-log scale implies that the notification documents
follow a Zipf-like distribution. We find that for our complete data-set the
value of 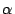 varies from 1.137 to 1.267 (in Figure 5,
the value of
varies from 1.137 to 1.267 (in Figure 5,
the value of 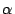 is 1.146). These values are higher than the
is 1.146). These values are higher than the 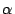 in the web proxy logs [7,10,14], and lower than (but close
to) the
in the web proxy logs [7,10,14], and lower than (but close
to) the 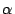 observed for popular web server logs [16].
observed for popular web server logs [16].
Figure 5:
Frequency of notification documents versus ranking in log-log scale (for August 21, 2000).
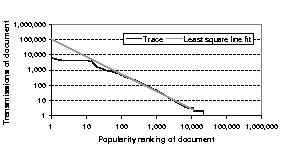 |
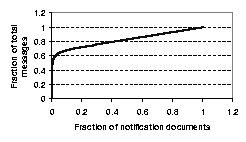
Figure 6 shows the cumulative distribution of notification
documents on August 21, 2000. The top 1% of notification documents (i.e.,
1704) account for 54.24% of the total notification messages. In the logs for
other days, the top 1% of notification documents account for 54.15% -
63.66% of the total messages. Such a high concentration of messages
containing popular documents suggests that using application-level
multicast [8,11,17,22] for popular documents would yield
significant savings in both bandwidth and server load.
Figure 6:
Cumulative distribution of notification messages to documents (for Aug 21, 2000).
 |
A possible optimization is to distribute a set of caches over the Internet
to form an overlay multicast tree rooted at the notification server. When a
notification message needs to be sent to multiple recipients simultaneously,
it can be sent over the overlay tree and also stored at the caches that it
traverses. These caches can help in offloading the retransmission work (say, due
to a client coming online) from the server: when the same copy of notification
needs to be sent at a later time, the caches closest to the receiver can
forward the message
Note that even though the current notification traffic is not significant, as
the popularity of notification services increases, bandwidth usage will become
an important factor for scaling the notification system. Consequently,
optimizations such as application-level multicast will become more important.
We also observed that the concentration of notification messages to documents
becomes less pronounced as the number of the documents considered increases.
For example, the top 7.6% - 42.0% of the documents account for 80% of the
total messages, and the top 45.1% - 71.0% of notifications account for 90%
of the total messages. This implies that a large performance benefit can be
obtained by multicasting only the most popular notification documents.



Next: User Behavior Analysis
Up: Notification Log Analysis
Previous: Notification Message Size and
Lili Qiu
2002-04-17


