In this section we consider a more abstract version of the problem and translate it to the problem of finding efficient authenticated data structures. The less theoretically inclined readers may skip directly to Section 4 that presents a self-contained description of such a data structure.
Put in an abstract framework, the problem we deal with is the following:
find a protocol between a non-trusted prover, P, and a verifier, V
for (non)membership in a set S,
where S is some finite set defined by a trusted party (the CA)
but not known to V.
Given an input x, P should prove either 
or 
,
The trusted party may change S dynamically,
but it is assumed to be fixed while P and V interact.
The prover has access to a data structure representing S along with some
approved public information about S, created by the trusted party prior to
setting x.
The non-trusted prover should have an efficient procedure for providing on-line
a short proof (e.g. of low order polynomial in 
) for the
appropriate claim for x.
Let U be a universe and S be a set such that 
.
Let 
be a data structure representing S.
.
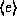The response to the query is a string 
where
, corresponding to 
, 
.
.
The response to the query is a string 
where
and p is a proof for a authenticated by
a CA.
where e is an element in 
.
The resulting data structure 
represents the set
.
where e is an element in S.
The resulting data structure 
represents the set
.
Definition:
A dictionary is a data structure 
representing S
supporting membership queries and update operations.
Definition:
An authenticated dictionary is a data structure 
representing S supporting authenticated membership queries and
update operations.
In our model, the set S is known both to the CA and the prover, P, but not to the verifier, V. The CA controls S and supplies P with the information needed to create an authenticated dictionary representing S.
Since an authenticated dictionary is dynamic, a mechanism for proving that an authenticated proof is updated is needed. Otherwise, a dishonest directory may replay old proofs. In our model we may assume either that CA updates occur at predetermined times, or, that the user issuing a query knows when the most recent update occurred. In any case, the verifier should be able to check the freshness of a proof p.
The parameters we are interested in regarding authenticated dictionaries are:
For a small universe U, one can afford computational work proportional to |U|. There are two trivial extremes with respect to the number of signed messages, the computation needed in authentication and verification, and the prover to verifier communication complexity:
the CA signs the appropriate message 
or 
.
To update 
, |U| signatures are supplied, regardless the number
of changed elements in 
.
An example of this solution is the certificate revocation system
reviewed in Section 2.2.
where for every 
, 
indicates whether 
.
satisfying 
for all 
.
.
An example is the certificate revocation lists reviewed
in Section 2.1.
In the following we describe a generic method for creating an authenticated
dictionary 
from a dictionary 
.
The overhead in membership queries and update operations is roughly a
factor of 
. In this construction we use a collision intractable
hash function.
Definition:
A collision intractable hash function is a function 
such that
it is computationally infeasible to find 
satisfying
.
Let 
be a dictionary of size 
representing a set S.
Let 
be the worst case time needed to a compute membership query or an
update operation respectively.
Let h be a collision intractable hash function, and 
be the time
needed to compute h on instances of U.
Consider the representation 
of S.
This may be e.g. a list of all the variables' values composing
, or, the way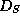 
is represented in random access memory.
The authenticated dictionary 
contains 
plus a
hash tree [17] whose nodes correspond to
, and a message signed by the CA
containing the tree root value and the time of update.
The hash tree is constructed as follows:
A balanced binary tree is created whose leaves are assigned the values
.
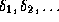Each internal node v is then assigned a value 
where
are the values assigned to v's children.
of 
accessed in the
computation. The proof consists of the values of all the nodes on the
path from the root to position i and their children.
The complexity of an authenticated membership query is thus
.
that were changed is re-computed (i.e. all paths
from a changed element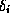 
to the root). The complexity of an
update operation is thus 
.
The general method of Section 3.2 for
creating dictionaries has a logarithmic (in 
) multiplicative
factor overhead.
The reason is that the internal structure of 
was not exploited in the authentication/verification processes.
Our goal is to create authenticated dictionaries based on efficient search data structures that save the logarithmic factor overhead. We denote these as authenticated search data structures.
CRTs reviewed in Section 2.3 save this
logarithmic factor in membership query complexity (but not in update where
the amount of computational work is not a function of the number of changes but
of the size of the revocation list).
In Section 4.1 we show how to create authenticated search
data structures based on search trees. An interesting open question is how
to construct more efficient authenticated search data structures, e.g. based
on hash tables, where membership query is processed in roughly 
.