Benchmark

Figure 11: Location estimation benchmark. The ground truth locations are at the centers of the circles. The mean of the measured locations are at the centers of the boxes. The edge length of each box is twice the standard deviation in each axis.

For the benchmark, we placed the observer at 22 locations on the grid $(80cm+i*100cm,80cm+j*100cm)$ in the base station coordinate system on the floor of the room. At each of the locations, we measured the location ten times by iteratively solving Equation System 10 as described in Section 4.2.

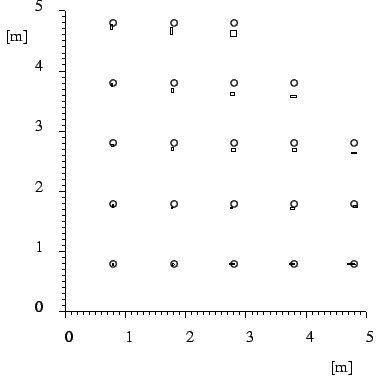
Figure 11 shows the base station coordinate system and the results of these measurements. Ground truth locations $(x,z)$ are indicated by circles. The mean of the computed location $(\bar{x}, \bar{z})$ is at the center of the small boxes. The edge length of each box is twice the standard deviation $s_x$ ($s_z$) of the measurements in the respective axis.

Please note that we determined ground truth locations using a cheap 5m tape measure, resulting in a maximum error of about $\pm1$cm in each axis. Also note that we did not perform out-lier rejection or any other statistical ``tricks'' to improve the mean values or standard deviations.

The mean relative offset of the mean locations from ground truth locations (i.e., $\vert\bar{x} - x\vert / x$) is 1.1% in the $x$ axis, and 2.8% in the $z$ axis. The overall mean relative offset of the mean locations from ground truth locations (i.e., $\vert(\bar{x}, \bar{z})-(x,z)\vert / \vert(x,z)\vert$ is 2.2%. The mean relative standard deviation (i.e., $s_x / x$) is 0.71% in the $x$ axis and 0.74% in the $z$ axis. The overall mean relative standard deviation (i.e., $s_{\vert(x,z)\vert} / \vert(x,z)\vert$) is 0.68%.

Note that while the mean standard deviations are almost the same for both axes, the mean relative offset of 2.8% in the $z$ axis is more than twice the value for the $x$ axis. We believe that this is due to the way we performed calibration. Firstly, some of the locations where we performed measurements are outside of the convex hull of the locations where we performed calibration. Additionally, we calibrated at only four locations and solved Equation System 12 directly in order to obtain the $C^\ast$ values. We expect better results by performing calibration using a larger set of reference locations and by using MMSE methods as mentioned in Section 4.2. We are currently working on improving the calibration part of our software.