![\includegraphics[width=3.0in]{convolutions}](img14.gif) |

![\includegraphics[width=3.0in]{convolutions}](img14.gif) |
Our tracking algorithm uses the convolutional neural network
architecture shown in Figure 5 to locate the salient
objects in its visual and auditory fields. The YUVD input images are
filtered with separate
![]() kernels, denoted by WY,
WU, WV, and WD respectively. This results in the filtered
images
kernels, denoted by WY,
WU, WV, and WD respectively. This results in the filtered
images ![]() ,
,
![]() ,
,
![]() ,
,
![]() :
:
| = | |||
| = | 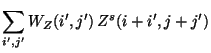 |
(2) |
| Xs(i,j) | = | ||
| (3) |
where the sigmoidal nonlinearity is given by
![]() .
Thus,
the saliency Xs is computed on a pixel-by-pixel basis using a
nonlinear combination of hidden units. The relative importance of the
different luminance, chromatic, motion, and auditory channels in the
overall saliency of an object is given by the scalar variables cY,
cU, cV, cD, and cA.
.
Thus,
the saliency Xs is computed on a pixel-by-pixel basis using a
nonlinear combination of hidden units. The relative importance of the
different luminance, chromatic, motion, and auditory channels in the
overall saliency of an object is given by the scalar variables cY,
cU, cV, cD, and cA.
With the bias term c0, the function g[Xs(i,j)] may be interpreted as the relative probability that the tracked object appears in location (i,j) at input resolution s. The final output of the neural network is then determined in a competitive manner by finding the location (im,jm) and scale sm of the best possible match:
| (4) |
After processing the visual and auditory inputs in this manner, head movements are generated in order to keep the maximally salient object located near the center of the field of view.