Unsupervised learning

The online learning algorithm described above allows our robot to rapidly adapt and correct mistakes when given supervisory feedback by a teacher. But there are many situations in which it is impossible for any teacher to be present. In these situations, would it still be possible for a system to adapt based upon raw sensory stimuli without being told the appropriate thing to do? This is generically quite a difficult problem, but there are some well-established algorithms that allow the system to continue to adapt even without a teacher. Generally, these unsupervised learning algorithms attempt to extract common sets of features present in the input data. The system can then use these features to reconstruct structured patterns from corrupted input data. This invariance of the system to noise allows for more robust processing in performing recognition tasks.

  

Figure: Three different unsupervised learning techniques applied to handwritten images of the digit "two." NMF learns a representation based upon the strokes of the digits, while VQ and PCA learn holistic representations. For each algorithm, the 25 columns of basis W are depicted as a $5 \times 5$ montage on the left, with their corresponding activations V in the middle. The reconstruction of the digit given by the product WV is displayed on the right of the figure.

One commonly used technique for building invariances into systems is to project the input data onto a few representative directions known as the principal components. This procedure called principal components analysis (PCA) has historically found widespread use in data compression, modeling, and classification systems [Jolliffe,Turk]. For an example of its application, consider the bottom portion of Figure 8. Here, a set of images of handwritten ``two'''s has been analyzed using PCA. The images are taken from the Buffalo Zip Code database [LeCun], and can formally be described by a $n \times m$ matrix X of pixel values. Each of the m=731 grayscale images is preprocessed to roughly center and align it within a $16 \times 16$ grid. The pixels are scaled such that white is equal to zero and black is equal to one. The n=256 pixel values are then arranged into a column of X, with each handwritten image forming a separate column. PCA factorizes the matrix X into the approximate form $X \approx WV$ where the matrix factors W and V are $n \times r$ and $r \times m$ in size, respectively. The columns of W correspond to an orthogonal basis set which can be used to reconstruct the original images in X using the coefficients in V. The left side of Figure 8 displays the r=25different columns of W, which are then multiplied by a particular set of coefficients in V to form the reconstruction image on the right.

PCA is able to efficiently reconstruct the original data X using the limited number r of bases because it uses a representation that is distributed across all of the matrix factors. Some of the bases in Wresemble common distortions of ``two'''s such as translations and rotations, so the PCA representation is able to capture this global variability in the data. However, this representation utilizes both positive and negative combinations of all the available bases in W. This implies that the reconstruction involves finely tuned cancellations among the different bases, so it is difficult to visualize exactly how most of the columns in W contribute to a robust representation.

In contrast, vector quantization (VQ) is another unsupervised learning technique that categorizes the input data in terms of prototypes rather than orthogonal basis vectors. VQ may be thought of as applying a quantizing error correction to the data in order to remove small perturbations in the input. Formally, it can again be described as an approximate matrix factorization $X \approx WV$ where the columns in matrix V of activations are constrained to be unary (exactly one element in each column is equal to one, all the other elements are zero). In the middle portion of Figure 8, the effect of this constraint can be seen as forcing the VQ factorization to learn various templates of different types of ``two'''s. In this case, reconstruction merely involves choosing the most similar prototype, and the representation is extremely sparse since only a single element of V is active.

The top portion of Figure 8 shows our new matrix factorization algorithm that decomposes the images into their representative parts. It achieves this by utilizing nonnegativity as a constraint on the components of the matrix factors W and V[Lee]. As seen in the figure, nonnegative matrix factorization (NMF) learns to decompose the image data into their constituent parts, corresponding to the different strokes of a ``two.'' To approximate a particular two, the appropriate strokes are summed together to form the reconstruction. This is in sharp contrast to the holistic features found by PCA and VQ. Note that NMF finds a decomposition into localized parts even though no prior information about the topology of the images was built into the input data, i.e. the rows of matrix Xcould have been arbitrarily scrambled and the NMF algorithm would have yielded the same results.

NMF also combines some of the representational advantages of PCA and VQ. Since many of the parts are used to form the reconstruction, NMF has the combinatorial expressiveness of a distributed representation. But because the nonzero elements of W and V are all positive, NMF allows only additive combinations. So unlike PCA, no cancellations can occur. On the other hand, the nonnegativity constraint causes almost half of the coefficients in V to go to zero, resulting in a sparse coding of the input. Thus, NMF learns a parts-based representation of the data that is sparse as well as distributed [Foldiak,Olshausen].

  

Figure: Multiplicative update rules for nonnegative matrix factorization. The accuracy of the current approximation $X \approx WV$ enters the learning through the quotient X_ik/(WV)_ik. It can be shown that these rules maximize the objective function $\sum_{i=1}^n \sum_{k=1}^m [X_{ik} \log(WV)_{ik} - (WV)_{ik}]$.

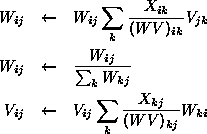Analytically, the NMF algorithm can be derived from a probabilistic generative model that incorporates Poisson noise [Hinton]. This model has previously been used in the deconvolution of astronomical images that have been blurred by the atmosphere and the telescope [Richardson,Lucy]. NMF may thus be considered a generalization of this technique to blind deconvolution. By maximizing the likelihood of this probabilistic model, the NMF learning rule for nonnegative matrix factorization is obtained [Dempster,Saul]: Given a data matrix X, the matrix factors W and V are first initialized to random positive values. The factors are then updated using the multiplicative update rules shown in Figure 9, which guarantees that the likelihood of the data X is increased. This procedure is then iterated until an optimal factorization $X \approx WV$ is learned.