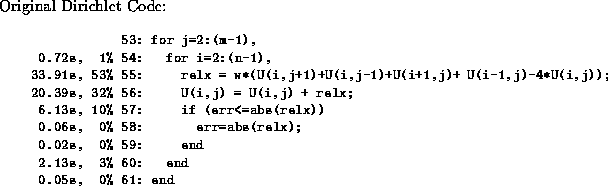A Case for Source-Level Transformations in MATLAB
Vijay Menon
Department of Computer Science
Cornell University
Ithaca, NY 14853
vsm@cs.cornell.edu
https://www.cs.cornell.edu/Info/People/vsm
Keshav Pingali
Department of Computer Science
Cornell University
Ithaca, NY 14853
pingali@cs.cornell.edu
https://www.cs.cornell.edu/Info/Projects/Bernoulli
Abstract:
In this paper, we discuss various performance overheads
in MATLAB codes and propose different program transformation strategies
to overcome them. In particular, we demonstrate that high-level source-to-source
transformations of MATLAB programs are effective in obtaining substantial
performance gains regardless of whether programs are interpreted or later
compiled into C or FORTRAN. We argue that automating such transformations
provides a promising area of future research.
Introduction
MATLAB is a programming language and development
environment which is popular in many application domains like signal processing
and computational finance that involve matrix computations. There are many
reasons for its popularity. First, MATLAB is a relatively high-level, untyped
language in which matrices are a built-in data type with a rich set of
primitive operations. Second, MATLAB programs are interpreted, making MATLAB
well-suited for prototyping code. (A compiler that translates MATLAB code
to C is available from MathWorks.) Third, the mex-file facility
makes it easy to invoke compiled C or FORTRAN functions from the MATLAB
interpreter. Finally, a full set of numerical and graphics libraries for
many applications domains like computational finance and signal processing
is available.
In general, there are overheads in the interpretation of programs in
high-level untyped languages like MATLAB that are not there in executing
code compiled from more conventional general-purpose languages like C or
FORTRAN. The most important of these overheads in MATLAB are the following.
-
Type and shape checking/dispatch: A variable can be introduced in
MATLAB programs without declaring its type or shape. Therefore, execution
of the MATLAB statement C = A*B; can require a computation as
simple as the product of two doubles or as complicated as the product of
two matrices A and B containing complex entries. The
interpreter must check types and shapes of operands in expressions for
compatibility, and dispatch to the right routine for carrying out the appropriate
operation. In traditional compiled languages, by contrast, the types and
shapes of matrices would be known to the compiler, so at runtime it is
only necessary to check that the number of columns of A is equal
to the number of rows of B.
-
Dynamic resizing: Since matrix sizes are not declared by the programmer,
the MATLAB interpreter allocates storage for a matrix on demand. If x
is a vector and an attempt is made to write to element x(i) where
i
is outside the current bounds of the vector, MATLAB allocates new storage
for a larger vector and copies over elements from the old vector into the
new storage. In FORTRAN or C, it is the responsibility of the programmer
to allocate a large enough matrix, and any attempt to write into a location
outside the index space of the matrix is an error.
-
Array bounds checking: The interpreter must check indexed accesses
of array elements to ensure that the access is within array bounds. In
conventional languages, static analysis can use array declarations to eliminate
bounds checks in many cases.
Techniques for reducing such interpretive overheads may be useful not only
for MATLAB programs but for programs in other domain-specific languages
many of which are also high-level, untyped, interpreted languages.
One approach is to translate MATLAB programs into programs in a conventional
language like C or FORTRAN, and attempt to eliminate these overheads when
compiling the C/FORTRAN code down to machine code. Several projects in
both academia and industry have taken this approach [2,4,5,9,13,18,19,20].
The mex-file interface described earlier can be used to invoke compiled
routines from the interpreter, permitting the programmer to use the familiar
MATLAB execution environment when running compiled code. However, as MATLAB
lacks variable declarations, generation of efficient C or FORTRAN requires
inference of types, shapes, and sizes. Unfortunately, compiler techniques
to automatically inference these properties without additional user input
have had limited success, as we discuss later in this paper.
In this paper, we will make the case for a very different approach to
reducing these overheads -- by using source-level transformations of MATLAB
code. The MATLAB community has developed a number of programmer tricks
[12] to enhance performance of MATLAB
codes. Surprisingly, these ideas have never been studied in the context
of compilation. The conventional compiler approach, described above, replaces
matrix operations with loops and indexed array accesses which are then
optimized using standard compiler technology. The source-level approach
advocated in this paper has the opposite effect since it replaces loops
and indexed accesses by high-level matrix operations! This is somewhat
counter-intuitive because type and shape checks, dynamic resizing and array
bounds checks are not explicit in high-level matrix programs, so it is
not obvious how these overheads are reduced by source-level transformations.
Nevertheless, we show that such source-level transformations are beneficial
regardless of whether the transformed code is executed by the MATLAB interpreter
or compiled to C or FORTRAN.
The rest of this paper is organized as follows. A more detailed discussion
of the overheads of interpreting MATLAB programs is given in Section 2.
Section 3 discusses how the MCC MATLAB
to C compiler attempts to eliminate these overheads. We also show the effect
of using various compiler flags in MCC such as the -i flag to
eliminate array bounds checks. Section 4
describes the source-level transformations of interest to us and evaluates
their effect on performance if the resulting code is interpreted by the
MATLAB interpreter. Section 5 argues
that source-level transformations are useful even if the transformed code
is compiled to native code by the MCC compiler. Section 6
compares our work with previous work. Section 7
gives a sketch of how these transformations can be performed automatically
by a restructuring compiler; details of an implementation can be found
in a companion paper [14].
Interpretation Cost of MATLAB
programs
Our work-load in this paper is the FALCON
benchmark set from the University of Illinois, Urbana [3].
This is a set of 12 programs from the problem domain of computational science,
and it contains iterative linear solvers (CG,QMR), finite-difference solvers
for pdes (CN,SOR), preconditioner computation for iterative linear solvers
(IC), etc. These benchmarks are described in Table 1.
In terms of MATLAB behavior, De Rose [3]
groups the programs into three separate categories.
Library-intensive
programs (CG, Mei, QMR, SOR) operate upon entire matrices via high-level
operations or routines. These codes contain few, if any, indexed accesses
into arrays.
Elementary-operation-intensive programs (CN, Di, FD,
Ga, IC) operate upon elements of matrices via loops. Virtually the entire
execution time is spent within loop nests operating on array elements.
Memory-intensive
programs (AQ, EC, RK) require considerable memory management overhead in
the form of dynamic resizing.
Table 1: Falcon Benchmark Suite
| Benchmark |
Flops |
Lines of Code |
| AQ |
Adaptive Quadrature Using Simpson's Rule |
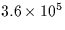 |
87 |
| CG |
Conjugate Gradient method |
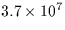 |
36 |
| CN |
Crank-Nicholson solution to the heat equation |
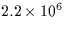 |
29 |
| Di |
Dirichlet solution to Laplace's equation |
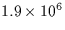 |
39 |
| FD |
Finite Difference solution to the wave equation |
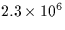 |
28 |
| Ga |
Galerkin method to solve the Poisson equation |
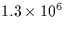 |
48 |
| IC |
Incomplete Cholesky Factorization |
 |
33 |
| Mei |
Generation of 3D-surface |
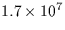 |
28 |
| EC |
Two body problem using Euler-Cromer method |
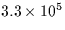 |
26 |
| RK |
Two body problem using 4th order Runge-Kutta |
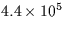 |
66 |
| QMR |
Quasi-Minimal Residual method |
 |
91 |
| SOR |
Successive Over-relaxation method |
 |
29 |
To measure the overhead of MATLAB interpretation, we would have liked
to execute our benchmark suite on a suitably instrumented MATLAB interpreter.
Unfortunately, the MathWorks interpreter is proprietary code, so we did
not have access to the source. We considered using publicly available MATLAB-like
interpreters and even instrumented one of them (Octave [6]),
but we found that they were sufficiently different from the MathWorks interpreter
that we could not draw meaningful conclusions about the performance of
the MathWorks interpreter from experiments on other interpreters. For example,
Octave is written in C++ and it uses the type-dispatch mechanism of C++
to implement the type checking and type dispatch required to execute MATLAB
matrix operations, so there is no direct way to measure this overhead.
Therefore, we had to make do with measuring the effect of program transformations
on overall performance. In this section, we describe the interpretive overheads
in more detail.
Type and Shape Checking
Unlike in C or FORTRAN, array variables in MATLAB programs can be introduced
without type declarations. Furthermore, a single variable can name matrices
of different types, shapes and sizes in different parts of the program.
The complexity that this introduces in the interpreter can be appreciated
by considering the assignment C = A*B. The type and shape of A
and B determine what computation is performed, so A*B
may refer to scalar-scalar multiplication, scalar-matrix multiplication,
or matrix-matrix multiplication where neither, either, or both of the arguments
are complex. Each possible combination specifies a different kind of computation.
Furthermore, the interpreter may also test for special cases where, for
example, one of the arguments is a row or column vector. While a vector
could be treated just as any other matrix, more efficient underlying implementations
exist for multiplying a matrix with a vector. Finally, the interpreter
may also have to test for legality; in the case of matrix-matrix multiplication,
the second dimension of A and the first dimension of B
must conform.
The MATLAB interpreter tests for all of the above possibilities each
time it encounters the * operator. However, examining the context
in which the expression occurs may reveal that the tests are redundant
or even completely unnecessary. Consider, for example, the
* operator
in the code:
for i = 1:n
y = y + a*x(i);
end
In this case, the cost of the checks is magnified in the interpreter as
they are performed in each iteration of the loop. However, note that x(i)
must be scalar, so no test is needed for it. Without additional information,
the type and shape of
a must be checked, but since a
is not modified within the loop, these properties need to be tested just
once, before the loop is executed.
Dynamic Resizing
In C or FORTRAN, storage for an array is allocated
before its elements are computed. Since there are no variable declarations
in MATLAB, storage for matrices and vectors is allocated incrementally
during program execution. An attempt to write into a matrix element outside
the bounds of the matrix causes the system to reallocate storage for the
entire matrix, copying over all elements from the old storage to the newly
allocated space. In loops, such memory management overheads can become
prohibitively expensive. Consider the following code:
for i = 1 : 10000
x(i)= i;
end
If x is initially undefined, the interpreter ``grows'' the vector
incrementally during loop execution. On a Sparc 20, the MATLAB interpreter
requires 14.2 seconds to execute this loop. However, it is clear before
the execution of the loop that x will grow to 10,000 elements.
If a vector x of this length is preallocated before the loop begins,
the loop executes in 0.37 seconds. In other words, repeated reallocation
in the loop slows the loop down by a factor of 40 in this case. Note that
the MATLAB interpreter only allocates the minimal amount of memory each
time. That is, if the vector is not preallocated before the loop, then,
on each iteration, the vector is reallocated into a memory block one element
larger.
Interestingly, this overhead in the MATLAB interpreter is not nearly
as significant for two dimensional arrays. Consider:
for i = 1 : 100
for j = 1 : 100
y(i,j)= i;
end
end
Again, we have an array eventually resized to hold 10,000 elements. However,
in this case, reallocation is not done on each iteration. In the first
iteration of the i loop, each iteration of the
j loop
resizes y by an additional column. In subsequent iterations of
the i loop, only the first iteration of the j loop causes
resizing. That iteration resizes
y to an 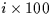 array. No other iteration triggers resizing. When y is initially
undefined, the interpreter requires 0.67 seconds to execute the above loop.
With y already allocated, the interpreter requires 0.48 seconds.
array. No other iteration triggers resizing. When y is initially
undefined, the interpreter requires 0.67 seconds to execute the above loop.
With y already allocated, the interpreter requires 0.48 seconds.
While it is clear that the two dimensional case requires fewer memory
reallocations, it is also true that it requires less data copying. In the
one dimensional case, iteration i requires copying of
i-1
data elements. An entire n2 element vector (where n=100
in our example) requires O(n4) copies. On the
other hand, for an equivalent size 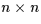 array, O(n2) copies are required for the first
row, and (i-1)*n copies are required for each subsequent
row i. Thus, the total number copies for the two dimensional array
is O(n3), asymptotically smaller than the one
dimensional case.
array, O(n2) copies are required for the first
row, and (i-1)*n copies are required for each subsequent
row i. Thus, the total number copies for the two dimensional array
is O(n3), asymptotically smaller than the one
dimensional case.
We conclude that the overhead of dynamic resizing is most important
when vectors are resized within loops.
Array Bounds Checking
Indexed accesses into arrays are another source of run-time checks in MATLAB.
Consider the following code:
x(i) = y(i);
The index i is checked to see if it is within the bounds of x
and y. If it is not within the bounds of x, it triggers
resizing as explained above. If it is not within the bounds of
y,
an error is reported.
As with type and shape checks, array bounds checks are often redundant,
as in the code:
for i = 2:n-1
x(i) = x(i-1)+x(i+1);
end
As before, the loop magnifies the overhead in the interpreter since three
checks are performed in each iteration. Clearly, the three checks performed
on the inner statement are redundant and can be collapsed to one. The array
x
must contain at least
i+1 elements for the statement to be legally
executed. The other two checks are subsumed by this check. Furthermore,
this remaining check need not be performed each iteration. If x
does not contain at least n elements, it is clear that the loop
cannot execute correctly.
Conventional Compilation
In this section, we examine the standard approach
to compiling away the interpretive overheads of MATLAB programs. The key
idea is to translate MATLAB code into C or FORTRAN programs, making type
checking, dynamic resizing, etc. explicit and therefore amenable to optimization.
We describe how the commercial MathWorks MCC compiler removes these overheads
and quantify its effectiveness.
Figure 1: MCC Compilation
 |
Type Inference
The MCC compiler attempts to eliminate type and shape checks through the
use of type and shape inference. The most sophisticated type inference
algorithm in the literature is the one in the FALCON compiler of De Rose
et al. [3,4].
The algorithm used in MCC is unpublished, but it appears to be similar.
The high level idea is to generate a system of type equations relating
the types and shapes of different variables and solve this system to determine
what these types and shapes can be. In particular, type and shape information
of inputs to expressions can be used to determine type and shape information
of outputs.
MCC operates at the level of single MATLAB functions, or
m-files
. When MCC performs inference on a function, the result is a forward propagation
algorithm in which the types and shapes of parameters and initialized local
variables in a program are used to determine the types of intermediate
and output variables. This, however, requires that type and shape information
be known for parameter variables; this is very difficult to infer automatically.
MCC's strategy is to generate two versions of compiled code for each function:
one that assumes that all inputs are real and one that assumes all are
complex. The compiler then inserts an initial run-time test at the beginning
of execution to determine if, in fact, all inputs are real.
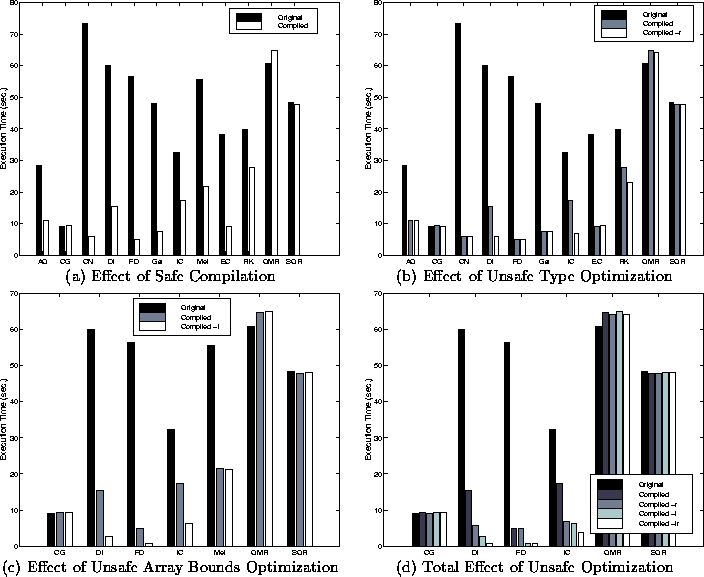
Figure 1a demonstrates the effectiveness
of the MCC compiler on the Falcon benchmarks on a Sun Sparc 20 machine.
For this set of measurements, no additional compile-time flags were used;
we will consider the effect of the two available optimization flags below.
Note that the compiler is most effective on loop-nest intensive codes.
On codes that are not loop intensive and predominantly utilize high-level
operations, such as CG, QMR and SOR, the compiler shows no performance
benefit. Surprisingly, the compiled code actually shows a slight slowdown
in two of these cases. In these cases, type checking and type dispatch
overhead is relatively insignificant compared to the time taken by the
actual computation.
Users may obtain better performance from MCC by directing it to perform
additional optimizations through the use of compilation flags. These optimizations,
unlike the default ones, are potentially unsafe since they may by illegal
for some programs. One unsafe optimization, triggered by a -r
option to the compiler, eliminates all tests for complex types and as a
result, generates code that assume all computation is on real numbers.
Obviously, this will not produce correct results for programs operating
on complex numbers. In the Falcon benchmarks, however, this optimization
is applicable on all but one of the benchmarks (Mei). Figure 1b
illustrates the effect of this optimization on the remaining eleven benchmarks.
There are noticeable performance gains in only three benchmarks (Di,
IC, RK). As mentioned above, the default behavior of MCC is to generate
two versions of compiled code in which one version assumes that all parameters
are real. In this version, the compiler is usually able to determine that
all intermediate and output variables are real as well. If this is the
case, the compiler will eliminate all checks for complex values. The only
additional advantage brought by the -r option is to eliminate
the initial test on input values which, as seen in Figure 1b,
is negligible. However, real input variables may not necessarily imply
real intermediate or output variables. Certain operations, such as a square
root, may produce complex values from real ones. In the presence of such
operations, type inference will fail to eliminate all type checks. For
example, in the Incomplete Cholesky benchmark, each column of the matrix
is scaled by the square root of the diagonal element. Even though the input
matrix is real, MCC is unable to infer that the result matrix will also
be real. In these cases, the
-r option, if applicable, can noticeably
enhance performance.
Array Bounds Optimization
The MCC compiler does not optimize away any array bounds checks. However,
the programmer can trigger bounds check elimination by using another compilation
flag (the -i flag). As described earlier, this is not safe even
for correct programs because out-of-bounds writes to an array are used
to trigger dynamic resizing. Furthermore, if the code has an out-of-bounds
read access, the compiled code generated by using this flag may produce
either incorrect results or catastrophic errors.
In the Falcon benchmarks, bounds check elimination is valid in seven
of the twelve programs (in the remainder, the interpreter either halts
with an error or produces incorrect results). The effect of using the
-i
compiler flag on these programs is shown in Figure 1c.
There are substantial improvements in three of the seven benchmarks for
which this flag is legal (Di, FD, IC). The remaining benchmarks predominantly
utilize higher-level functions and contain few, if any, subscripted references
to arrays.
Discussion
The overall effect of compilation, using compiler flags to eliminate type
and shape checks as well as array out of bounds checks where legal, is
shown in Figure 1d. Eliminating type checks
by using the -r flag is useful in the Di, IC and RK benchmarks
while elimination of array bounds checks by using the -i flag
is most effective in the Di, FD and IC benchmarks. Note that when a compiler
flag is unsafe for a program, it may still be possible to apply the corresponding
optimization to just a portion of the program. In the Galerkin benchmark,
for example, dynamic resizing occurs within the function, and so the -i
option will generate erroneous code. However, it does not occur within
the innermost loop, where array bounds checks are most expensive. Performance
measurements at this finer level of granularity require access to the MathWorks
interpreter and compiler.
Figure 2: Source-to-Source Optimizations
 |
Source-Level Optimizations
In this section, we discuss source-level
transformations of MATLAB programs and show how they can be used to reduce
interpretive overhead. At first glance, this may seem to be a counterintuitive
idea since the language provides no direct means of instructing an interpreter
when and when not to perform various checks. The key insight is that
these overheads are most significant in loops, so loops can be transformed
to eliminate interpretive overhead. In this section, we discuss three
different source-level transformations and show how they improve the efficiency
of our work-load. In the next section, we compare these performance improvements
with the performance improvements obtained by the MCC compiler.
Vectorization
Vectorization transforms loop programs into
high-level matrix operations. This is similar to vectorization for vector
supercomputers; in both cases, the key is to map a sequence of operations
on array elements into one or more high-level operations on entire arrays.
On vector hardware, these array operations can be executed more efficiently
than loops with scalar operations. A similar gain in efficiency is possible
in MATLAB interpretation. Loops slow down MATLAB programs by magnifying
the overhead of statements contained with in the loop. Any type checks
or array bounds checks performed on a statement within the loop will be
repeated for every iteration even though multiple checks may be redundant.
However, for higher level MATLAB operations that act on entire matrices
and vectors, these checks are performed only once. Hence, the performance
benefit of high level operations can be very large.
Figure 3: Effect of Vectorization on Galerkin Benchmark
 |
Consider the execution profile of the Galerkin benchmark in Figure
3a.
This loop nest represents a small portion of the program but it is clearly
the bottleneck in performance since 97% of the execution time of the entire
program is spent within this loop nest. However, the entire loop nest can
be vectorized by realizing that it is actually performing a vector-matrix-vector
multiplication. When this loop nest is replaced by equivalent matrix-vector
operations, the resulting profile is as shown in Figure 3b.
This transformation enhances the performance of the loop nest by a factor
of 250, and the performance of the entire benchmark is increased 100-fold!
Of course, vectorization is not always applicable. Many programs such
as CG and QMR in the Falcon suite already extensively utilize higher-level
operations and contain no for-loops. In other programs, such as the Dirichlet
code in Figure 4, expensive for-loops
exist but cannot be mapped to higher-level operations. In this case, the
dependences due to U prevent either of the for-loops from being
vectorized.
Figure 4: Dirichlet Benchmark
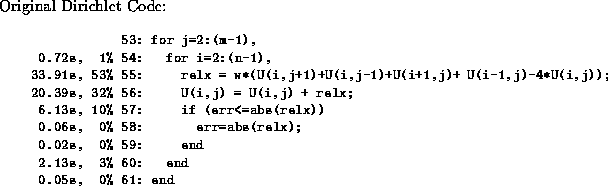 |
Vectorization is applicable to five of the twelve Falcon benchmarks.
The effects on each of these five programs is shown in Figure 2a.
In two programs (FD, Ga), the effects are dramatic since they result in
more than 30-fold improvements. In these cases, vectorizable loops were
responsible for nearly all the original execution time. In one case (Di),
the effect is minor. Here, the vectorizable loop took only a minor portion
of the original execution time.
Preallocation
As discussed in Section 2.2, resizing
of arrays can result in significant memory management overhead due to repeated
reallocation and copying. In many cases, the final size of the array can
be easily inferred. When this is the case, it is often safe to preallocate
the entire array at once. Consider the original code for the Euler-Cromer
program in Figure 5a.
Figure 5: Effect of Preallocation on Euler-Cromer Benchmark
 |
Figure 6: Effect of Expression Optimization on QMR Benchmark
 |
87% of program execution time is spent in the lines shown. In this case,
each of the arrays shown above is undefined prior to execution of this
loop, so the array is resized on each iteration of the loop. However, it
is clear in this case that ultimately, each array will be of length nstep.
There is no way to declare the size of a matrix in MATLAB, but an indirect
way to accomplish the same goal is to use the zeros operator that
creates an array of a desired size and initializes its values to 0. Therefore,
statements of the following form can be used to avoid resizing:
rplot = zeros(1,nstep);
When preallocation is done for all arrays, we obtain the profile shown
in Figure 5b. Each of these statements
is now significantly faster (by a factor of more than seven). As a result,
the entire benchmark is faster by a factor of roughly four.
Unfortunately, simple preallocation as above cannot eliminate all instances
of dynamic resizing. For example, in the AQ code, the final size of the
array cannot be determined a priori. While more complex strategies such
as preallocating an estimated size or explicitly growing the array in an
exponential manner may reduce this cost, we have not attempted to do so
in this paper.
Finally, even when preallocation can be done, the performance benefits
will differ from case to case. The Euler-Cromer code represents a relatively
extreme case since several one dimensional arrays are resized, and the
final size of each (over 6,000) is fairly large. As mentioned in Section
2.2,
the resizing overhead is significantly less with two dimensional arrays.
Dynamic array resizing occurs in five of the twelve Falcon benchmarks.
In four of these cases (AQ is the exception), the eventual size of resized
arrays is easily determined. Figure 2b
highlights the effect of preallocation on these four benchmarks.
Expression Optimization
Finally, we consider a source-level transformation not directly motivated
by MATLAB overheads. Instead, we are motivated by the naivete of MATLAB's
evaluation process. Unlike an optimizing compiler, the MATLAB interpreter
does not consider the best manner in which to compute an expression. Instead,
it blindly computes it in the most straightforward manner. Consider the
profile information from the QMR benchmark in Figure 6a.
In an eighty line program, this single statement requires 70% of the
entire execution time. Closer examination of this program reveals that
beta
is a scalar, w_tld, q, and w are column vectors,
and A is a two-dimensional matrix. Thus, the subexpression A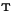 *q
is clearly the most expensive to compute, requiring O(n2)
work to perform a matrix-vector product. However, the MATLAB interpreter
will also compute a temporary matrix for the value A
*q
is clearly the most expensive to compute, requiring O(n2)
work to perform a matrix-vector product. However, the MATLAB interpreter
will also compute a temporary matrix for the value A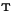 ,
requiring an additional n2 space and and copy operations,
before it computes the product. Clearly, a temporary matrix should not
be necessary to perform the computation. Unfortunately, the MATLAB language
does not provide a way of expressing this computation as a single operation,
thus forcing the evaluation of the subexpression. While a source-level
transformation cannot directly avoid this, it can reduce the cost by realizing
that (q
,
requiring an additional n2 space and and copy operations,
before it computes the product. Clearly, a temporary matrix should not
be necessary to perform the computation. Unfortunately, the MATLAB language
does not provide a way of expressing this computation as a single operation,
thus forcing the evaluation of the subexpression. While a source-level
transformation cannot directly avoid this, it can reduce the cost by realizing
that (q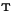 *A)
*A)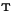 is an equivalent and less expensive expression. Although this expression
requires two transpose operations, in both cases vectors are transposed
instead of matrices. Note the profile of the transformed code in Figure
6b.
is an equivalent and less expensive expression. Although this expression
requires two transpose operations, in both cases vectors are transposed
instead of matrices. Note the profile of the transformed code in Figure
6b.
The result is a better that twenty-fold increase on that single statement
and a three-fold increase on the entire benchmark. These kinds of transformations
that exploit the semantics of matrix operations are not feasible at the
C/FORTRAN level.
Comparison of Source-level Transformations
and Compilation
Figure 7: Source-Level Transformations and Compilation
 |
In this section, we compare the separate and the combined effects of
source-level and compiler optimizations. Figure 7
shows the performance benefits realized by different combinations of optimizations.
The first three sets of bars represent the original MATLAB code, MCC compiled
code with no unsafe optimizations, and MCC compiled code with all unsafe
optimizations legal for that particular benchmark activated. The second
three sets of bars represent the same measurements taken on source-level
transformed code.
There are a number of interesting observations to be made. First, the
performance improvement from source-level optimizations is quite comparable
with performance improvement from MCC compiler optimizations. In four cases
(CG, EC, RK, SOR), source-level optimizations have a roughly similar effect
on performance when compared to safe MCC optimizations. In four other cases
(FD, Ga, IC, QMR), source-level optimizations are better by a factor of
two or more. In two of these cases (Ga, QMR), source-level optimizations
outperform even unsafe optimizations by a wide margin! On the other hand,
the remaining four cases (AQ, CN, Di, Mei) profit much more from compilation
than source-level optimizations. These codes all contained expensive loops
performing scalar operations that could not be eliminated by vectorization.
Second, source-level optimizations are best viewed as being complementary
to compiler optimizations. The last two set of bars in Figure 7
illustrate the combined effect of source-level and compiler optimizations.
For programs in which source-level transformations result in improved interpreted
performance, these transformations result in improved compiled performance
as well. Across all benchmarks, the combination of optimizations provides
the best performance. In five cases (CN, FD, Ga, IC, EC), the combination
significantly exceeds the effect of either source-level or compiler optimizations
alone. Each of the different source-level transformations provides benefits
not currently provided by MCC.
-
When vectorization can generate high-level operations such as those in
BLAS, as in Galerkin, efficient underlying libraries may be utilized by
both interpreter and compiler. These libraries outperform code generated
by a C or FORTRAN compiler on the corresponding loops.
-
Although preallocation does not significantly effect the performance of
every benchmark where it is applicable (see Figure 2b),
it permits the otherwise unsafe compiler optimization of array bounds removal.
The effect of this optimization after preallocation on, for example, Crank-Nicholson
is dramatic.
-
Algebraic optimizations such as the one used on QMR have no equivalent
in MCC. These types of optimizations dependent on matrix properties cannot
easily be applied at the lower level of a C compiler.
We conclude from these results that source-level transformations are key
to obtaining good performance from MATLAB codes for both interpreted and
compiled execution.
Related Work
As mentioned in the introduction, several
MATLAB compilers have been developed or are under development. Each of
these compilers translates MATLAB into a lower language such as FORTRAN,
C, or C++.
There are two commercial MATLAB compilers. MCC [13]
is from the The MathWorks, developers of MATLAB itself, and is the compiler
studied in this paper. MCC can handle most features in MATLAB 5 and generates
C code. MATCOM [9], originally developed
at the Israel Institute of Technology and now offered by MathTools, also
handles most features of MATLAB 5 and generates C++ code. Both MCC and
MATCOM are capable of generating either stand-alone programs or mex-files
that may be linked back into the MATLAB interpreter. As far as we are aware,
these are the only two publicly available compilers and the only two capable
of generating mex-files.
There are a handful of compilers under development in academia. Falcon
[4] from University of Illinois, translates
MATLAB 4 into FORTRAN-90. Menhir [2], from
Irisa in France, focuses on a retargetable code generator capable of generating
C or FORTRAN for sequential or parallel machines. MATCH [18],
from Northwestern, uses MATLAB to directly target special purpose hardware.
Three other compilers, CONLAB [5], from
the University of Umea in Sweden, Otter [19],
from Oregon State University, and one other from Northwestern University
[20], explicitly target parallel machines
by generating message passing code from MATLAB.
Of all of these compilers, only Falcon appears to consider source-level
transformations [4,11]
along the lines of those described in this paper. However, these transformation
must be applied interactively via a user tool and are not part of the automatic
compilation process. Furthermore, the source-level transformations are
limited to syntactic pattern match and replacement, so they do not provide
a general solution for optimizations such as vectorization and preallocation.
A similar type of idiom recognition appears to be performed by optimizing
FORTRAN preprocessors such as KAPF [10] and
VAST-2 [16]. These tools do attempt to detect
matrix products in loop nests in order to generate BLAS operations. However,
pattern matching is inherently limited in its ability to do this; neither
processor is able to detect a vector-matrix-vector product written as in
the Galerkin code shown in Section 4.1.
There has been compiler research on performing optimizations similar
to the source-level transformations presented in this paper. Vectorization
for vector supercomputers has been studied extensively over the past three
decades, for example in [1,21].
However, this work largely focuses on point-wise assignments and scalar
operations between arrays and, occasionally, on reduction operations rather
than the higher-level operations available in MATLAB. The problem of array
bounds removal, similar to preallocation and directly applicable to MATLAB,
has been studied in the context of conventional languages [7].
Finally, a handful of projects [8,15,17]
have developed parallel toolkits for use with the MATLAB interpreter. These
toolkits allow MATLAB programs to directly access message passing libraries
for interprocessor communication. To gain any performance benefit, users
must parallelize their MATLAB programs using provided MATLAB-level message
passing constructs.
Conclusion and Future Work
Source-level transformations provide
an effective means of obtaining performance for MATLAB programs, regardless
of whether they are interpreted or later compiled. These transformations
are capable of eliminating many inefficiencies that currently available
MATLAB compilers are unable to optimize away.
We have implemented an automatic tool to perform source-level optimizations
as part of the FALCON project, a joint project of Cornell University and
the University of Illinois, Urbana. A detailed description of this tool
can be found in a companion paper [14].
Incorporating both source-level and lower-level optimizations into an interpreter
in a just-in-time manner is an ongoing effort.
References
-
1
-
R. Allen and K. Kennedy.
Automatic translation of FORTRAN programs to vector form.
ACM Transactions on Programming Languages and Systems, 9(2):491-542,
October 1987.
-
2
-
S. Chauveau and F. Bodin.
Menhir: An environment for high performance MATLAB.
In 4th Workshop on Languages, Compilers, and Run-time Systems for
Scalable Computers, Pittsburgh, PA, May 1998.
-
3
-
L. De Rose.
Compiler Techniques for MATLAB programs.
PhD thesis, University of Illinois at Urbana-Champaign, 1996.
-
4
-
L. De Rose, K. Gallivan, E. Gallopoulos, B. Marsolf, and D. Padua.
FALCON: A MATLAB interactive restructuring compiler.
In Languages and Compilers for Parallel Computing, pages 269-288.
Springer-Verlag, August 1995.
-
5
-
P. Drakenberg, P. Jacobson, and B. Kagstrom.
A CONLAB compiler for a distributed memory multicomputer.
In 6th SIAM Conference on Parallel Processing for Scientific Computing,
volume 2, pages 814-821, 1993.
-
6
-
J. Eaton.
GNU Octave.
https://www.che.wisc.edu/octave
.
-
7
-
R. Gupta.
A fresh look at optimizing array bound checking.
In Programming Languages, Design and Implementation. ACM SIGPLAN,
Jun 1990.
-
8
-
J. Hollingsworth, K. Liu, and P. Pauca.
Parallel Toolbox for MATLAB.
Wake Forest University, 1996.
https://www.mthcsc.wfu.edu/pt/pt.html
.
-
9
-
Y. Keren.
MATCOM: A MATLAB to C++ translator and support libraries.
Technical report, Israel Institute of Technology, 1995.
-
10
-
Kuck and Associates, Inc.
KAP for IBM Fortran and C.
https://www.kai.com/product/ibminf.html
.
-
11
-
B. Marsolf.
Techniques for the Interactive Development of Numerical Linear Algebra
Libraries for Scientific Computation.
PhD thesis, University of Illinois at Urbana-Champaign, 1997.
-
12
-
The MathWorks, Inc.
How Do I Vectorize My Code?
https://www.mathworks.com/support/tech-notes/v5/1100/1109.shtml
.
-
13
-
The MathWorks, Inc.
MATLAB Compiler, 1995.
-
14
-
V. Menon and K. Pingali.
High-level semantic optimization of numerical codes.
In International Conference of Supercomputing (ICS'99), June
1999.
-
15
-
V. Menon and A. Trefethen.
MultiMATLAB: Integrating MATLAB with high performance parallel computing.
In Supercomputing, November 1997.
-
16
-
Pacific Sierra Research Corporation.
VAST-2 for XL Fortran.
https://www.psrv.com/vast/vast_xlf.html
.
-
17
-
S. Pawletta, T. Pawletta, and W. Drewelow.
Comparison of parallel simulation techniques - MATLAB/PSI.
Simulation News Europe, 13:38-39, 1995.
-
18
-
The MATCH Project.
A MATLAB compilation environment for distributed heterogeneous adaptive
computing systems.
https://www.ece.nwu.edu/cpdc/Match/Match.html
.
-
19
-
M. Quinn, A. Malishevsky, and N. Seelam.
Otter: Bridging the gap between MATLAB and ScaLAPACK.
In 7th IEEE International Symposium on High Performance Distributed
Computing, August 1998.
-
20
-
S. Ramaswamy, E. W. Hodges, and P. Banerjee.
Compiling MATLAB programs to ScaLAPACK: Exploiting task and data parallelism.
In Proc. of the International Parallel Processing Symposium,
April 1996.
-
21
-
M. Wolfe.
High Performance Compilers for Parallel Computing.
Addison-Wesley Publishing Company, 1995.
About this document ...
A Case for Source-Level Transformations in MATLAB
This document was generated using the
LaTeX2HTML
translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos
Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -no_navigation paper.
The translation was initiated by Vijay Menon on 8/24/1999
Footnotes
-
...
-
This work was supported by NSF grants CCR-9720211, EIA-9726388 and ACI-9870687.
Vijay Menon
8/24/1999