 |

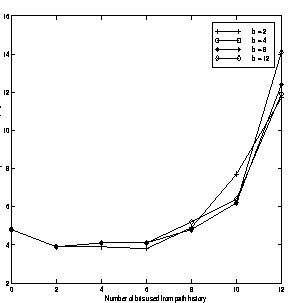
The bit width of the path history buffer, h that constitutes the least significant bits used to index the target buffer was varied and its effect on the misprediction rate was investigated. This was performed to study the relative importance of the path history and program counter information. Figure 8 shows the results of this for an 8K entry target buffer using javac for different values of b. It is observed that the misprediction rate decreases, when h increases from 0 to 6. When h is increased further, the misprediction rates increase. Since the 8K target buffer is indexed using a fixed size 13-bit index, the number of bits from the program counter used in the index reduces as the value of h increases. This indicates that the call site location is relatively more important than just the path history information. The target address being primarily determined by the call site location and path history providing only additional information in the prediction accounts for this behavior. Table 4 shows the relative importance of the path history and call site location. It is observed that using only the 13-bit call site location to index the 8K target buffer, a misprediction rate of 4.9% is achieved. The misprediction rate increases to 12.9% when 12 bits of path history and 1-bit of the call site location are used for javac.
 |
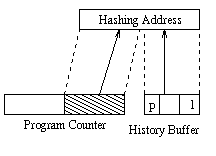
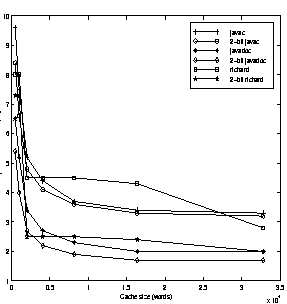
In order to utilize both the program counter and the path history bits more effectively for a fixed size target buffer, a XOR hashing scheme shown in Figure 9 was investigated. The XOR hashing function helps in combining more information from the program counter and the path history bits as compared to the concatenation scheme. Here, a bitwise XOR of the program counter and the path history buffer bits is performed to obtain the hashing address. Then, the least significant bits of the hashing address are used to index the target buffer. Two replacement strategies were studied to update the target buffers using the global XOR scheme. These schemes are the same as those studied to update the BTB. It was observed that the 2-bit scheme performs better for the XOR scheme for most of the benchmarks. Figure 10 shows the results for the javac benchmark. The 2-bit strategy is referred to as the XOR scheme in the rest of the paper. The effectiveness of the XOR scheme as compared to the concatenation scheme is shown in Table 4. It is observed that for an 8K target buffer, the minimum misprediction rate using the concatenation scheme is 4.1% compared to the 3.6% using the XOR scheme for javac.
 |
| S | Javac Misses (%) | Richards Misses (%) | ||||
| 8K | 16K | 32K | 8K | 16K | 32K | |
| 0 | 4.9 | 4.7 | 4.7 | 23.4 | 23.4 | 23.4 |
| 4 | 4.2 | 3.8 | 3.7 | 4.0 | 4.0 | 4.0 |
| 6 | 4.1 | 3.7 | 3.5 | 4.0 | 4.0 | 3.9 |
| 8 | 5.2 | 4.4 | 3.7 | 3.8 | 3.8 | 3.8 |
| 10 | 6.4 | 5.0 | 4.1 | 8.7 | 8.0 | 1.8 |
| 12 | 12.9 | 7.7 | 5.6 | 14.2 | 8.7 | 8.7 |
| xor | 3.6 | 3.3 | 3.2 | 2.4 | 2.3 | 2.0 |
Next, the effect of path length on the misprediction rate of
the XOR scheme was investigated. In order to vary the path length, the number of bits b written
from each target address into the history buffer was varied. If s bits are required to index the
tagless target buffer and p is the path length, b was chosen such that
![]() .
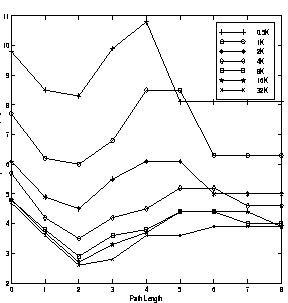
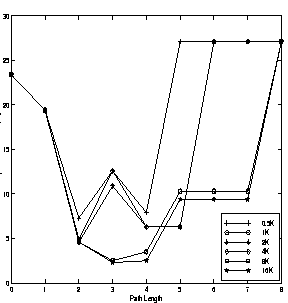
Figures 11 and 12
show the results of this study for javac and richards benchmarks respectively. The
misprediction rate for javac exhibits a similar trend as the fully associative unconstrained
target buffer size. It achieves the minimum misprediction rates
for a path length of two. For the richards benchmark the misprediction rates are the least
for a path length of two when target buffer sizes are small(0.5K to 2K). When target buffer size is
increased (4K to 32K), the minimum misprediction value is achieved for a path length of three. Thus,
a longer path length improves misprediction rate with an increase in the target buffer size. This is due to
the greater number of bits of each target address constituting the index portion of the target buffer
for a given path length.
.
Figures 11 and 12
show the results of this study for javac and richards benchmarks respectively. The
misprediction rate for javac exhibits a similar trend as the fully associative unconstrained
target buffer size. It achieves the minimum misprediction rates
for a path length of two. For the richards benchmark the misprediction rates are the least
for a path length of two when target buffer sizes are small(0.5K to 2K). When target buffer size is
increased (4K to 32K), the minimum misprediction value is achieved for a path length of three. Thus,
a longer path length improves misprediction rate with an increase in the target buffer size. This is due to
the greater number of bits of each target address constituting the index portion of the target buffer
for a given path length.
 |
 |