Using Fault Injection and Modeling to Evaluate the Performability of Cluster-Based Services1

Kiran Nagaraja, Xiaoyan Li, Ricardo Bianchini, Richard P. Martin, Thu D. Nguyen
Department of Computer Science, Rutgers University
110 Frelinghuysen Rd, Piscataway, NJ 08854
{knagaraj, xili, ricardob, rmartin, tdnguyen}@cs.rutgers.edu

Abstract. We propose a two-phase methodology for quantifying the performability (performance and availability) of cluster-based Internet services. In the first phase, evaluators use a fault-injection infrastructure to measure the impact of faults on the server's performance. In the second phase, evaluators use an analytical model to combine an expected fault load with measurements from the first phase to assess the server's performability. Using this model, evaluators can study the server's sensitivity to different design decisions, fault rates, and environmental factors. To demonstrate our methodology, we study the performability of 4 versions of the PRESS Web server against 5 classes of faults, quantifying the effects of different design decisions on performance and availability. Finally, to further show the utility of our model, we also quantify the impact of two hypothetical changes, reduced human operator response time and the use of RAIDs.

Introduction

Popular Internet services frequently rely on large clusters of commodity computers as their supporting infrastructure [5]. These services must exhibit several characteristics, including high performance, scalability, and availability. The performance and scalability of cluster-based servers have been studied extensively in the literature, e.g., [2,5,7]. In contrast, understanding designs for availability, behavior during component faults, and the relationship between performance and availability of these servers have received much less attention.

Although today's service designers are not oblivious to the importance of high availability, e.g., [5,12,28], the design and evaluation of availability is often based on the practitioner's experience and intuition rather than a quantitative methodology.

In this paper, we advance the state-of-the-art by developing a 2-phased methodology that combines fault-injection and analytical modeling to study and quantify the performability - a metric combining performance and availability - of cluster-based servers. In the first phase of our methodology, the server is benchmarked for performance and availability both in the presence and absence of faults. To support systematic fault-injection, we introduce Mendosus, a fault-injection and network emulation infrastructure designed specifically to study cluster-based servers. While evaluators using our methodology are free to use any fault-injection framework, Mendosus provides significant flexibility in emulating different LAN configurations and is able to inject a wide variety of faults, including link, switch, disk, node, and process faults.

The second phase of our methodology uses an analytical model to combine an expected fault model [23,32], measurements from the first phase, and parameters of the surrounding environment to predict performability. Designers can use this model to study the potential impact of different design decisions on the server's behavior. We introduce a single performability measure to enable designers to easily characterize and compare servers.

To show the practicality of our methodology, we use it to study the performability of PRESS, a cluster-based Web server [7]. A significant benefit of analyzing PRESS is that, over time, the designers of PRESS have accumulated different versions with varying levels of performance. Using our methodology, we can quantify the impact of changes from one version to another on availability, and therefore, performability, producing a more complete picture than just the previous data on performance. For example, a PRESS version using TCP for intra-cluster communication achieves a higher overall performability score even though it does not perform as well as a version using VIA. We also show how our model can be used to predict the impact of design or environmental changes; in particular, we use our model to study PRESS's sensitivity to operator coverage and using RAIDs instead of independent SCSI disks.

The remainder of the paper is organized as follows. The next section describes our methodology and performability metric. Section 3 describes our fault-injection infrastructure. Section 4 describes the basic architecture of the PRESS server and its different versions. Section 5 presents the results of our fault-injection experiments into the live server. Section 6 describes the results of our analytical modeling of PRESS. We discuss the lessons we learned in Section 7. Section 8 describes the related work. Finally, in Section 9 we draw our most important conclusions.

Methodology and Metric

Our methodology for evaluating servers' performability is comprised of two phases. In the first phase, the evaluator defines the set of all possible faults, then injects them (and the subsequent recovery) one at a time into a running system. During the fault and recovery periods, the evaluator must quantify performance and availability as a function of time. We currently equate performance with throughput, the number of requests successfully served per second, and define availability as the percentage of requests served successfully. In the second phase, the evaluator uses an analytical model to compute the expected average throughput and availability, combining the server's behavior under normal operation, the behavior during component faults, and the rates of fault and repair of each component.

Phase 1: Measuring Performance Under Single-Fault Fault Loads

There are two tricky issues when injecting faults. First, when measuring the server's performance in the presence of a particular fault, the fault must last long enough to allow all stages in the model of phase 2 to be observed and measured. The one exception to this guideline is that a server may not exhibit all model stages under certain faults. In these cases, the evaluator must use his understanding of the server to correctly determine which stages are missing (and later setting the time of the stage in the abstract model to 0). Second, a benchmark must be chosen to drive the server such that the delivered throughput is relatively stable throughout the observation period (except for transient warm up effects). This is necessary to decouple measured performance from the injection time of a fault.

Phase 2: Modeling Performability Under Expected Fault Loads

**Figure 1:** *The 7-stage piece-wise linear model specified by our methodology for evaluating the performability of cluster-based servers.*
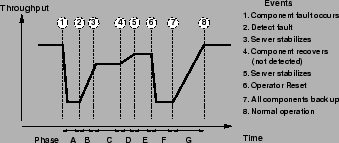
$\begin{figure}\begin{center} \epsfig{figure=../figs/model-timeline.eps,width=3in}\end{center}\end{figure}$

Our model for describing average performance and availability is built in two parts. The first part of the model describes the system's response to each fault in 7 stages. The second part combines the effects of each fault along with the MTTF (Mean Time To Failure) and MTTR (Mean Time To Recovery) of each component to arrive at an overall average availability and performance.

Per-Fault Seven-Stage Model. Figure 1 illustrates our 7-stage model of service performance in the presence of a fault. Time is shown on the X-axis and throughput is shown on the Y-axis. Stage A models the degraded throughput delivered by the system from the occurrence of the fault to when the system detects the fault. Stage B models the transient throughput delivered as the system reconfigures to account for the fault; the system may take some time to reach a stable performance regime because of warming effects. We model the throughput during this transient period as the average throughput for the period. After the system stabilizes, throughput will likely remain at a degraded level because the faulty component has not yet recovered, been repaired or replaced. Stage C models this degraded performance regime. Stage D models the transient performance after the component recovers. Stage E models the stable performance regime achieved by the service after the component has recovered. Note that in the figure, we show the performance in E as being below that of normal operation; this may occur because the system is unable to reintegrate the recovered component or reintegration does not lead to full recovery. In this case, throughput remains at the degraded level until an operator detects the problem. Stage F represents throughput delivered while the server is reset by the operator. Finally, stage G represents the transient throughput immediately after reset.

For each stage, we need two parameters: (i) the length of time that the system will remain in that stage, and (ii) the average throughput delivered during that stage. The latter is measured in phase 1. The former is either measured, or is a parameter that must be supplied. For example, the time that a service will remain in stage B assuming that the fault last sufficiently long is typically measured; the time a service will remain in stage E is typically a supplied parameter.

Sometimes stages may not be present or may be cut short. For example, if there are no warming effects, then stages B, D, and G would not exist. In practice, we set the length of time the system is in such a state to zero. If the assumed MTTR of a component is less than the measured time for stages A and B, then we assume that B is cut short when the component recovers. The evaluator must analyze the measurements gathered in phase 1, the assumed parameters of the fault load, and the environment carefully to correctly parameterize the model.

Modeling Overall Availability and Performance. Having defined the server's response to each fault, we now must combine all these effects into an average performance and average availability metric. To simplify the analysis, we assume that faults of different components are not correlated, fault arrivals are exponentially distributed, and faults queue at the system so that only a single fault is in effect at any point in time. These assumptions allow us to add together the various fractions of time spent in degraded modes. If T_n is the server throughput under normal operation, c is the faulty component, T_c^s is the throughput of each stage s when fault c occurs, and D_c^s is the duration of each stage, our model leads to the following equations for average throughput (AT) and average availability (AA):

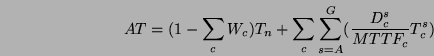
$\begin{displaymath}AT = (1 - \sum_c W_c) T_n + \sum_c \sum_{s=A}^G (\frac{D_c^s}{MTTF_c} T_c^s)\end{displaymath}$

where $W_c = (\sum_{s=A}^G D_c^s) / MTTF_c$ . In plain English, W_c is the expected fraction of the time during which the system operates in the presence of fault c. Thus, the $(1 - \sum_c W_c) T_n$ factor above computes the expected throughput when the system is free of any fault, whereas the $\sum_{s=A}^G (\frac{D_c^s}{MTTF_c} T_c^s)$ factor computes the expected average throughput when the system is operating with a single fault of type c. Note that T_n represents the offered load assuming that the server is not saturated under normal operation, so AT / T_n computes the expected fraction of offered requests that are successfully served by the system.

It is interesting to consider why the denominator of W_c is just MTTF_c instead of MTTF_c + MTTR_c. The equation for W_c is correct as it is because the assumptions listed above imply that when a fault occurs and is on-going, any other fault could arrive and queue at the system, including a fault to the same component. The impact on our model is that we compute the fraction of downtime as $\frac{MTTR}{MTTF}$ , not as the more typical $\frac{MTTR}{MTTF+MTTR}$ . In practice, the numerical impact of this difference is minimal, because MTTF » MTTR.

Limitations. A current limitation of our model is that it does not capture data integrity faults; that is, faults that lead to incorrect data being served to clients. Rather it assumes the only consequence of component faults is degradation in performance or availability. While this model is obviously not general enough to describe all cluster-based servers, we believe that it is representative of a large class of servers, such as front-end servers (including PRESS) and other read-only servers.

Another limitation of our model is that it is based on the measured response to single faults; the model can thus only capture multiple simultaneous faults as a sequence of non-overlapping faults. If we assume that faults are independent, then the introduced error is bounded by the probability of there being two or more jobs in a single multi-class server queue when the fault arrival and repair processes are viewed in a queuing-theoretic framework. Intuition tells us that the probability of seeing multiple simultaneous faults for practical MTTFs and MTTRs should be extremely low. Determining the probability of simultaneous faults exactly is not straightforward, but our initial approximations (assuming the rates in this paper) show that we can expect around 2 multi-fault events per year. On the other hand, there are indications that failures are not always independent [22,35], as well as anecdotal evidence that baroque, complex failures are not uncommon [14]. These observations imply that the independence assumptions in our model will result in optimistic predictions for the frequency of multi-fault scenarios [33]. Unfortunately, there is no study that quantifies such correlations for cluster-based Internet services. In the future, we may extend our methodology for designers to test their service's sensitivity to sets of potentially correlated faults.

Performability Metric

Despite much work that studies both performance and availability (e.g., [21,30]), there is arguably no single performability metric for comparing systems. Thus, we propose a combined performability metric that allows direct comparison of systems using both performance and availability as input criteria. Our approach is to multiply the average throughput by an availability factor; the challenge, of course, is to derive a factor that properly balances both availability and performance. Because availability is often characterized in terms of ``the number of nines'' achieved, we believe that a log-scaled ratio of how each server compares to an ideal system is an appropriate availability measure, leading to the following equation for performability:

where A_I is an ideal availability, T_n is the throughput under normal operation, AA is the average availability, and P is the performability of the system. A_I must be less than 1 but can otherwise be chosen by the service designers to represent the availability that is desired for the service, e.g., 0.99999.

This metric is an intuitive measure for performability because it scales linearly with both performance and unavailability. Obviously, if performance doubles, our performability metric doubles. On the other hand, if the unavailability decreases by a factor of 2, then performability also roughly doubles. The intuition behind this relationship between unavailability (u) and performability is that we can approximate $\log(1-u)$ as -u when u is small. Further, if the service designers wish to weigh one factor more heavily than the other, their importance can easily be adjusted by multiplying each term by a separate constant weight.

Mendosus

Mendosus is a fault injection and network emulation infrastructure designed to support phase 1 of our methodology. Mendosus addresses two specific problems that service designers are faced with today: (1) how to assemble a sufficiently representative test-bed to test a service as it is being built, and (2) how to conveniently introduce faults to study the service's behavior under various fault loads. In this section, we first briefly describe Mendosus's architecture and then discuss the fault models used by the network, disk, and node fault injection modules, which are used extensively in this work, in more detail.

Architecture

Mendosus is comprised of four software components running on a cluster of PCs physically interconnected by a Giganet VIA network: (1) a central controller, (2) a per-node LAN emulator module, (3) a set of per-node fault-injection kernel modules, and (4) a per-node user-level daemon that serves as the communication conduit between the central controller and the kernel modules.

The central controller is responsible for deciding when and where faults should be injected and for maintaining a consistent view of the entire network. When emulation starts, the controller parses a configuration file that describes the network to be emulated and components' fault profiles. It forwards the network configuration to the daemon running at each node of the cluster. Then, as the emulation progresses, it uses the fault profiles to decide what faults to inject and when they should be injected. It communicates with the per-node daemons as necessary to effect the faults (and subsequent recovery). Note that while there is one central controller per emulated system, it does not limit the scalability of Mendosus: the controller only deals with faults and does not participate in any per message operations.

The per-node emulation module maintains the topology and status of the virtual network to route messages. To emulate routing in Ethernet networks, a spanning tree is computed for the virtual network. Each emulated NIC is presented as an Ethernet device; a node may have multiple emulated NICs. When a packet is handed to the Ethernet driver from the IP layer, the driver invokes the emulation module to determine whether the packet should be forwarded over the real network (and which node it should be forwarded to). The emulation module determines the emulated route that would be taken by the packet. It then queries the network fault-injection module whether the packet should be forwarded. If the answer is yes, the packet is forwarded to the destination over the underlying real network. The emulation module uses multiple point-to-point messages to emulate Ethernet multicast and broadcast. A leaky bucket is used to emulate Ethernet LANs with different speeds.

Finally, the set of fault-injection kernel modules effect the actual faults as directed by the central controller. Currently, we have implemented 3 modules, allowing faults to be injected into the network, SCSI disk subsystems, and individual nodes. The challenge in implementing these subsystems is to accurately understand the set of possible real faults and the fault reporting that percolates from the device through the device drivers, operating systems, and ultimately, up to the application. We describe the fault models we have implemented in more details in the next several sections.

Network Fault Model

The network fault model includes faults possible for network interface cards, links, hubs, and switches. For each component, a fault can lead to probabilistic packet loss or complete loss of communication. In addition, for switches and hubs, partial failures of one or more ports are possible. All faults are transient although a permanent fault can be injected by specifying a down time that is greater than the time required to run the fault-injection experiment.

Our fault-injection module is embedded within an emulated Ethernet driver. Recall that the emulated driver also includes our LAN emulator module, which contains all information needed to compute the route that each packet will take. Fault injection for the network subsystem is straightforward when the communication protocol already implements end-to-end fault detection. Faults are effected simply by checking whether all components on the route are up. If any are down, the packet is simply dropped. If any components are in an intermittent faulty state, then the packet is dropped (or sent) according to the specified distribution.

Recall that the central controller is responsible for instructing the network fault injection modules on when, where, and what to inject dynamically. Instructions from the central controller are received by the local daemon and passed to the injection module through the ioctl interface. The fault-injection and emulation modules must work together in that faults may require the emulation module to recompute the routing spanning tree. The central controller is responsible for determining when a set of faults leads to network partition. When this occurs, the controller must choose a root for each partition so that the nodes within the partition can recompute the routing spanning tree.

SCSI Disk Fault Model

Table 1: SCSI faults that Mendosus can currently inject.

Fault	Characteristic	OS Masking of Fault
Disk hang	Sticky	Unmasked
Disk offline	Sticky	Unmasked
Power failure	Sticky	Unmasked
Read fault	Sticky	Unmasked in Linux
Write fault	Sticky	Unmasked in Linux
Timeout	Transient	Unmasked
Parity errors	Transient	Masked
Bus busy	Transient	Masked
Queue full	Transient	Masked

The SCSI subsystem is comprised of the hard disk device, the host adaptor, a SCSI cable connecting the two, and a hierarchy of software drivers. Higher layers in the system try to mask faults at lower levels and only the fatal faults are explicitly passed up the hierarchy. We model faults that are noticeable by the application either by explicitly forcing error codes reported by the operating system, or implicity by extended delays in the completion of disk operations.

We broadly classify possible faults into two categories: transient and sticky (non-transient). For transient faults, the disk system recovers after a small finite interval (on order of a few seconds in most cases); sticky faults require human intervention for correction. Examples of transient faults are SCSI timeouts, and recoverable read and write faults, whereas disk hang, external SCSI cable unplugging and power failures (to external SCSI housing) are sticky failures.

The impact of these faults on the system depends on whether the OS can and does attempt to mask the fault from the application through either a retry or some other corrective action. For example, a parity error in the SCSI bus is typically masked by the OS through a retry, whereas the OS does not attempt to mask a disk hang due to a firmware bug because this error likely requires external intervention. Masked faults may introduce tolerable delays, whereas unmasked faults may lead to stalling of execution. However, some unmasked faults, if recognized, can be handled by using alternate resources. This involves implementing smarter, fault-aware systems.

Table 1 shows the faults that we can inject into the SCSI subsystem. The fault injection module is interposed between the adapter-specific low-level driver and the generic mid-level driver. Instructions for injecting faults received from the central controller by the local daemon are communicated to the fault injection module through the proc filesystem. To effect faults, the fault injection module traps the queuing of disk operation requests to the low-level driver and prevents or delays the operation that should be faulty from reaching the low-level driver. In the former case, the module must return an appropriate error message.

The mid-level driver implements an error handler which diagnoses and corrects rectifiable faults reported by the low-level driver, either by retrying the command or by resetting the host, bus, device, or a combination of these. The unmasked read and write faults, caused by bad sectors unremappable by the disk controller are not handled by the upper drivers or the file system in Linux. This causes read and write operations to the bad sector to fail forever. The disk can be taken offline by the new error handler code introduced in 2.2+ Linux kernels when all efforts to rectify an encountered error fail. The disk can also be offline if it has been taken out for maintainence or replacement.

Node and Process Fault Models

Currently, our node and process fault model is simple. Mendosus can inject three types of node faults: hard reboot, soft reboot, and node freeze. All can be either transient or permanent, depending on the specified fault load. In the application process fault model, Mendosus can inject an application hang or crash. We may consider more subtle node/process faults such as memory corruption in the future.

This fault model is implemented inside the user-level daemon at each node. For our study of PRESS, the server process on each node is started by the daemon. An application hang is injected by having the daemon send a SIGSTOP to the server process. The process can be restarted if the fault is transient by sending a SIGCTN to it. A process crash is injected by killing the process.

Node faults are introduced using an APC power management power strip. Reboot faults are introduced by having the daemon on the failing node contact the APC power strip to power cycle that node. In the case of a soft reboot, the daemon can ask the APC for a delayed power cycle and then run a shutdown script. For a node freeze, the daemon directs a small kernel module to spin endlessly to take over the CPU for some amount of time.

The PRESS Server

PRESS is a highly optimized yet portable cluster-based locality-conscious Web server that has been shown to provide good performance in a wide range of scenarios [7,8]. Like other locality-conscious servers [27,2,4], PRESS is based on the observation that serving a request from any memory cache, even a remote cache, is substantially more efficient than serving it from disk, even a local disk. In PRESS, any node of the cluster can receive a client request and becomes the initial node for that request. When the request arrives at the initial node, the request is parsed and, based on its content, the node must decide whether to service the request itself or forward the request to another node, the service node. The service node retrieves the file from its cache (or disk) and returns it to the initial node. Upon receiving the file from the service node, the initial node sends it to the client.

To intelligently distribute the HTTP requests it receives, each node needs locality and load information about all the other nodes. Locality information takes the form of the names of the files that are currently cached, whereas load information is represented by the number of open connections handled by each node. To disseminate caching information, each node broadcasts its action to all other nodes whenever it replaces or starts caching a file. To disseminate load information, each node piggy-backs its current load onto any intra-cluster message.

Communication Architecture. PRESS is comprised of one main coordinating thread and a number of helper threads used to ensure that the main thread never blocks. The helper threads include a set of disk threads used to access files on disk and a pair of send/receive threads for intra-cluster communication.

PRESS can use either TCP or VIA for intra-cluster communication. The TCP version basically has the same structure of its VIA counterpart; the main differences are the replacement of the VI end-points by TCP sockets and the elimination of flow control messages, which are implemented transparently to the server by TCP itself.

Reconfiguration. PRESS is often used (as in our experiments) without a front-end device, relying on round-robin DNS for initial request distribution to nodes. Some versions of PRESS have been designed to tolerate node (and application process) crashes, removing the faulty node from the cooperating cluster when the fault is detected and re-integrating the node when it recovers. The detection mechanism when TCP is used for intra-cluster communication employs periodic heartbeat messages. To avoid sending too many messages, we organize the cluster nodes in a directed ring structure. A node only sends heartbeats to the node it points to. If a node does not receive three consecutive heartbeats from its predecessor, it assumes that the predecessor has failed.

Fault detection when VIA is used for intra-cluster communication is simpler. PRESS does not have to send heartbeat messages itself since the communication subsystem promptly breaks a connection on the detection of any fault. Thus, a node assumes that another node has failed if the VIA connection between them is broken. In this implementation, nodes are also organized in a directed ring, but only for recovery purposes.

In both cases, temporary recovery is implemented by simply excluding the failed node from the server. Multiple node faults can occur simultaneously. Every time a fault occurs, the ring structure is modified to reflect the new configuration.

The second and final step in recovery is to re-integrate a recovered node into the cluster. When using TCP, the rejoining node broadcasts its IP address to all other nodes. The currently active node with lowest id responds by informing the rejoining node about the current cluster configuration and its node id. With that information, the rejoining node can reestablish the intra-cluster connections with the other nodes. After each connection is reestablished, the rejoining node is sent the caching information of the respective node. When the intra-cluster communication is done with VIA, the rejoining node simply tries to reestablish its connection with all other nodes. As connections are reestablished, the rejoining node is sent the caching information of the respective nodes.

Table 2: Versions of PRESS available for study.

Version	Main Features
I-PRESS	Independent servers
TCP-PRESS	Cooperative caching servers using TCP for intra-cluster communication
ReTCP-PRESS	Cooperative caching servers using TCP for intra-cluster communication and dynamic reconfiguration
VIA-PRESS	Cooperative caching servers using VIA for intra-cluster communication and dynamic reconfiguration

Versions. Several versions of PRESS have been developed in order to study the performance impact of different communication mechanisms [8]. Table 2 lists the versions of PRESS that we consider in this paper. The base version of PRESS, I-PRESS, is comprised of a number of independent Web servers (based on the same code as PRESS) answering client requests. This is equivalent to simply running multiple copies of Apache, for example. The other versions cooperate in caching files and differ in terms of their concern with availability, and the performance of their intra-cluster communication protocols.

Case Study: Phase 1

We now apply the first phase of our methodology to evaluate the performability of PRESS. We first describe our experimental testbed, then show a sampling of PRESS's behavior under our fault loads. Throughout this section, we do not show results for I-PRESS as they entirely match expectation: the achieved throughput simply depends on how many of the nodes are up and able to serve client requests.

Experimental Setup

In all experiments, we run a four-node version of PRESS on four 800 MHz PIII PCs, each equipped with 206 MB of memory and 2 10,000 RPM 9 GB SCSI disks. Nodes are interconnected by a 1 Gb/s cLAN network. We can communicate with TCP or VIA over this network. PRESS was allocated 128 MB on each node for its file cache; the remainder of the memory was sufficient for the operating system. In our experiments, PRESS only serves static content and the entire set of documents is replicated at each node on one of the disks. PRESS was loaded at 90% of saturation and set to warm up to this peak throughput over a period of 5 minutes. Note that, because we are running so close to saturation and PRESS already implements sophisticated load balancing, we do not apply a front-end load distributor. Under such high load and little excess capacity, the front-end would not prevent the loss of requests in the event of a fault.

The workload for all experiments is generated by a set of 4 clients running on separate machines connected to PRESS by the same network that connects the nodes of the server. The total network traffic does not saturate any of the cLAN NICs, links, and switch, and so the interference between the two classes of traffic is minimal in our setup. Finally, Mendosus's network emulation system allows us to differentiate between intra-cluster communication and client-server communication when injecting network-related faults. Thus, the clients are never disturbed by faults injected into the intra-cluster communication.

Each client generates load by following a trace gathered at Rutgers; we chose this trace from several that Carrera and Bianchini previously used to evaluate PRESS's performance because it has the largest working set [7]. Results for other traces are very similar. To achieve a particular load on the server, each client generates a stream of requests according to a Poisson process with a given average arrival rate. Each request is set to time out after 2 seconds if a connection cannot be completed and to time out after 6 seconds if, after successful connection, the request cannot be completed.

Table 3: Fault loads for PRESS performability study. For transient faults, the given times represent the duration of the faults.

Subsystem	Fault	Characteristics
Network	Link down	Transient - 5, 180 secs
	Switch down	Transient - 5, 180 secs
Disk	SCSI timeout	Transient - 120 secs
	Disk hang	Sticky
	Read faults	Sticky
	Write faults	Sticky
Node	Hard reboot	Transient - 180 secs
	Node freeze	Transient - 180 secs
Application	Process crash	Transient - 180 secs
	Process hang	Transient - 180 secs

**Figure 2:** *Effects of transient switch faults. Pairs of vertical lines represent the start and end times of injected faults.*
$\begin{figure}\begin{center} \begin{tabular}{ccc} \epsfig{file=../figs/faults/n... ...s/net-sw_down.RCFG-VIA.eps, width=2in}\\ \end{tabular}\end{center}\end{figure}$

Finally, Table 3 lists the set of faults that we inject into a live PRESS system to study its behavior. Faults fall into four categories: network, disk, node, and application. Note that these generic faults can be caused by a wide variety of reasons for a real system; for example, an operator accidentally pulling out the wrong network cable would lead to a link failure. We cannot focus on all potential causes because this set is too large. Rather, we focus on the class of failures as observed by the system, using an MTTF that covers all potential causes of a particular fault. This set is comprehensive with respect to PRESS in that it covers just about all resources that PRESS uses in providing its service.

Network Faults

**Figure 3:** *Effects of transient SCSI time-out faults. Pairs of vertical lines represent the start and end times of injected faults.*
$\begin{figure}\begin{center} \begin{tabular}{ccc} \epsfig{file=../figs/faults/s... .../scsi-timeout.RCFG-VIA.eps, width=2in}\\ \end{tabular}\end{center}\end{figure}$

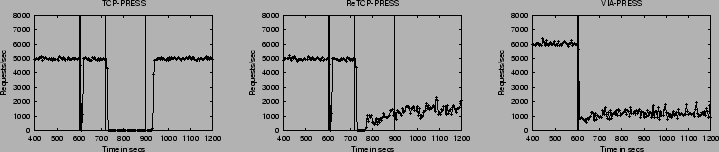
In this section, we study PRESS's behavior under network faults. Figure 2 shows the effects of a transient switch fault. We first discuss what happened in each case, then make an interesting general observation.

TCP-PRESS behaved exactly as expected: throughput drops to zero a short time after the occurrence of the fault because the queues for intra-server communication fill up as the nodes attempt to fetch content across the faulty switch. Throughput stays at zero until the switch comes back up. For ReTCP-PRESS, the first switch fault leads to the same behavior as TCP-PRESS; the reconfiguration code does not activate because the fault is sufficiently short that no heartbeat is lost. The longer switch fault, however, triggers the reconfiguration code, leading ReTCP-PRESS to reconfigure into 4 groups of singleton. The detection time is determined by the heartbeat protocol, which uses a DEADTIME interval of 15 seconds (3 heartbeats). For VIA-PRESS, the switch fault is detected almost immediately by the device driver, which breaks all VIA connections to unreachable nodes. This immediately triggers the reconfiguration of VIA-PRESS into four sub-clusters.

Interestingly, ReTCP-PRESS and VIA-PRESS do not reconfigure back into a single cluster once the switch returns to normal operation. This surprising behavior arises from a mismatch between the fault model assumed by the reconfigurable versions of PRESS and the actual fault. These versions of PRESS assume that nodes fail but links and switches do not. Thus, reconfiguration occurs at startup and on loss of 3 heartbeats, but re-integration into a single group only happens at startup. If a cluster is splintered as above, they never attempt to rejoin. Return to full operation thus would require the intervention of an administrator to restart all but one of the sub-clusters. This, in effect, make these reconfigurable versions less robust than the basic TCP-PRESS in the face of relatively short transient faults, and points to the importance of the accuracy of the fault model used in designing a service.

Finally, we do not show results for the link/NIC fault here because they essentially lead to the same behaviors as above.

Disk Faults

Recall that each server machine contains two SCSI disks, one holding the operating system and the second the file set being served by PRESS. We inject faults into only the second disk to minimize the interference from operating system-related disk accesses (e.g., page swapping) while observing the behavior of PRESS under disk faults.

**Figure 4:** *Effects of a node crash. Pairs of vertical lines represent the start and end times of injected faults.*
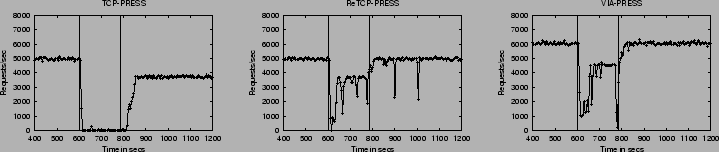$\begin{figure}\begin{center} \begin{tabular}{ccc} \epsfig{file=../figs/faults/n... ...sh.RCFG-VIA.eps, width=2in}\\ \end{tabular}\normalsize\end{center}\end{figure}$

**Figure 5:** *Effects of one PRESS process crash. Pairs of vertical lines represent the start and end times of injected faults.*
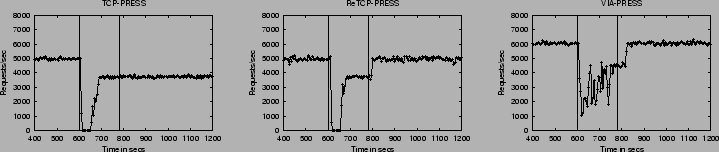$\begin{figure}\begin{center} \begin{tabular}{ccc} \epsfig{file=../figs/faults/a... ...sh.RCFG-VIA.eps, width=2in}\\ \end{tabular}\normalsize\end{center}\end{figure}$

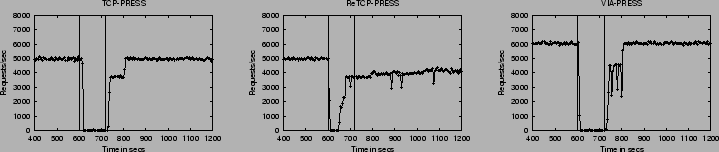
Figure 3 shows PRESS's behavior under SCSI timeouts. TCP-PRESS and VIA-PRESS behave exactly as one would expect. When the fault lasts long enough, all disk helper threads become blocked and the queue between the disk threads and the main thread fills up. When this happens, the main thread itself becomes blocked when it tries to initiate another read. Once one of the nodes grinds to a halt, then the entire server eventually comes to a halt as well. When the faulty disk recovers, the entire system regains its normal operation.

ReTCP-PRESS, on the other hand, interprets the long fault as a node fault and so splinters into sub-clusters, one with 3 nodes and one singleton. This splintering of the server cluster is caused by missing heartbeats. Similar to the argument for TCP-PRESS and VIA-PRESS above, when all disk threads block because of the faulty disk, the main thread also eventually blocks when it tries to initiate yet one more read. In this case, however, the main thread is also responsible for sending the heartbeat messages. Thus, when it blocks, its peers do not get any more heartbeats and so assume that that node is down; at this point, the reconfiguration code takes over, leading to the splinter.

We do not show results for disk hang, read and write faults because the behaviors are much as expected.

Node Faults

Figure 4 shows the effects of a hard reboot fault. Because it is not capable of reconfiguration, TCP-PRESS grinds to a halt while the faulty node is down. When the node successfully reboots, however, the open TCP connections of the three non-faulty nodes with the recovered node break. At this point, the PRESS processes running on these nodes realize that something has happened to the faulty node and stop attempting to coordinate with it. Thus, server operation restarts with a cluster of 3 nodes. When the faulty node successfully completes the reboot sequence, Mendosus starts another PRESS process automatically. However, since TCP-PRESS cannot reconfigure, correct operation with a cluster of 4 nodes cannot take place until the entire server is shutdown and restarted.

ReTCP-PRESS and VIA-PRESS behave exactly as expected. Operation of the server grinds to a halt until the reconfiguration code detects a fault. The three non-faulty nodes recover and operate as a cooperating cluster. When the faulty node recovers and the PRESS process has been restarted, it joins in correctly with the three non-faulty processes and throughput eventually returns to normal.

We do not show results for a node freeze because they are similar to those for a SCSI time-out. TCP-PRESS and VIA-PRESS degrades to 0 throughput during the fault but recovers fully. ReTCP-PRESS splinters and cannot recover fully.

Application Faults

Figure 5 shows the effects of an application crash, which are similar to those of a node crash. The one difference is that TCP-PRESS recovers from 0 throughput more rapidly because it can detect the fault quickly through broken TCP connections. The effects of an application hang are exactly the same as a node freeze.

Table 4: Faults and their MTTFs and MTTRs.

Fault	MTTF	MTTR
Link down	6 months	3 minutes
Switch down	1 year	1 hour
SCSI timeout	1 year	1 hour
Hard reboot	2 weeks	3 minutes
Process crash	1 month	3 minutes

Table 5: Example throughput and duration of the phases in our model for VIA-PRESS for two different faults. Note that for some types of faults, some phases collapse into a single phase or are not used.

Phase	Switch Fault		Application Crash
	Thruput	Duration	Thruput	Duration
	(reqs/sec)	(secs)	(reqs/sec)	(secs)
A	892.40	75	1889.10	10
B	-	0	3143.55	145
C	1106.70	3525	4537.60	25
D	-	0	4789.13	45
E	1209.60	300	-	0
F	0.0	300	-	0
G	3017.00	300	-	0

**Figure 6:** *(a) Average modeled throughput and (b) modeled unavailability (1 - availability).*
$\begin{figure}\begin{center} \begin{tabular}{cc} \epsfig{figure=../figs/modeled... ...bf (b)}\\ \end{tabular}\end{center}\vspace{-0.25in} \vspace{0.1in}\end{figure}$

Case Study: Phase 2

We now proceed to the second phase of our methodology: using the analytical model to extrapolate performability from our fault-injection results. We first compare the performance, availability, and performability of the different versions of PRESS. Then, we show how we can use the model to evaluate design tradeoffs, such as adding a RAID or increasing operator support.

Parameterizing the Model

We parameterize our model by using the data collected in phase one, the fault load shown in Table 4, and a number of assumptions about the environment. Since we cannot list all data extracted from phase 1 here because of space constraints, we refer the interested reader to https://www.panic-lab.rutgers.edu/Research/mendosus/. Table 5 provides a flavor of this data, listing the throughput and duration of each phase of our 7-stage model for VIA-PRESS for two types of faults. The MTTFs and MTTRs shown in Table 4 were chosen based on previously reported faults and fault rates [13,16,32]. Note that we do not model all the faults that we can inject because there are no reliable statistics for some of them, e.g., application hangs. Finally, our environmental assumptions are that operator response time for stage E is 5 minutes and cluster reset time for stage F is 5 minutes. Recall from Section 5.1 that G, the warm up period, was also set to 5 minutes.

Modeling Results

Figure 6(a) shows the expected average throughput in the face of component faults for the 4 PRESS versions. As has been noted in previous work, the locality-conscious request distribution significantly improves performance. The use of user-level communication improves performance further.

Figure 6(b) shows the average unavailability of the different versions of PRESS. Each bar includes the contributions of the different fault types to unavailability. These results show that availability is somewhat disappointing, on the order of 99.9%, or ``three nines''. However, recall that the servers were operating near peak; any loss in performance, such as losing a node or splintering, results in an immediate loss in throughput (and in many failed requests). A fielded system would reserve excess capacity for handling faults. Exploring this tradeoff between performability and capacity is a topic for our future research.

Comparing the systems, observe that I-PRESS achieves the best availability because there's no coordination between the nodes. TCP-PRESS is almost an order of magnitude worse than I-PRESS; this is perhaps expected since TCP-PRESS does a very poor job of tolerating and recovery from faults. More interestingly, ReTCP-PRESS gives better availability than VIA-PRESS. Looking at the bars closely, we observe that this is because ReTCP-PRESS is better at tolerating SCSI timeouts. This is fortuitous rather than by design: as previously discussed, when a SCSI timeout occurs, the heartbeats are delayed in ReTCP-PRESS, causing the cluster to reconfigure and proceed without the faulty node. VIA-PRESS does not reconfigure because the communication subsystem does not detect any fault.

**Figure 7:** *Performability of each version of PRESS when A_I=0.99999 or ``five nines availability.''*
$\begin{figure}\begin{center} \epsfig{figure=../figs/modeled-perf-4node.eps,height=1.6in}\end{center}\end{figure}$

Finally, Figure 7 shows the performability of the different PRESS versions. We can see that although the locality-aware, cooperative nature of TCP-PRESS does deliver increased performance, the lack of much, if any, fault-tolerance in its design reduces availability significantly, giving it a lower performability score than I-PRESS. The superior performance of the ReTCP and VIA versions of PRESS make up for their lower availability over I-PRESS. Again, the fact that ReTCP gives a better performability score than VIA-PRESS is the fortuitous loss of heartbeats on SCSI timeouts. Thus, we do not make any conclusion based on this difference (rather, we discuss the nature of heartbeats in Section 7).

Quantifying Design Tradeoffs. Analytical modeling of faults and their phases enables us to explore the impact of our server designs on performability. Thus, we examine two alternative design decisions to the ones we have explored so far.

The first design change is to reduce the operator coverage. In the previous model, the mean time for an operator to respond when the server entered a non-recoverable state was 5 minutes. This represents the PRESS servers running under the watchful eyes of operators 24x7. However, as this is quite an expensive proposition, we reduced the mean response to 4 hours and observed the performability impact.

**Figure 8:** *Impact of reducing the mean operator response from 5 minutes to 4 hours and adding a more reliable disk subsystem.*
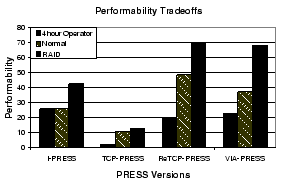$\begin{figure}\begin{center} \epsfig{figure=../figs/modeled-tradeoffs.eps,height=1.6in}\end{center}\end{figure}$

Figure 6(b) suggests that disks are a major cause of unavailability. In this second design change, we added a much more reliable disk subsystem, e.g., a RAID. We modeled the better disk subsystem by increasing the mean time to failure of the disks by a factor of five, but keeping the MTTR of the disks the same.

Figure 8 shows the performability impact of these two design changes. The center bar represent the same ``basic'' results as in Figure 7. The left most bar is the basic system with a 4-hour operator response, and the right is the basic system enhanced with a RAID.

Our modeling results show that running the cooperative versions in an environment with quick operator response is critical (unless fault recovery can be improved significantly): the performability of all the cooperative versions become less than that of I-PRESS. On the other hand, our results show that I-PRESS is insensitive to operator response time as expected.

The performability models also demonstrate the utility of a highly-reliable disk subsystem. Figure 8 show that by purchasing increasingly reliable disk subsystems, performability of all versions of PRESS is enhanced, e.g., approximately 84% for VIA-PRESS. In fact, ReTCP-PRESS and VIA-PRESS achieve virtually the same performability in the presence of this more sophisticated disk subsystem. These results suggest that the overall system impact of redundant disk organizations, such as RAIDs, is substantial.

Scaling to Larger Cluster Configurations. We now consider how to scale our model to predict the performability of services running on larger clusters. Such scaling may be needed because systems are typically not designed and tested at full deployment scale. We demonstrate the scaling process by scaling our measurements collected on the 4-node cluster to predict PRESS's performability on 8 nodes, which is the largest configuration we can achieve using our current testbed for validation. We then compare these results against what happens if the fault-injections and measurements were performed directly on an 8-node system.

Essentially, our model depends on three types of parameters: the mean time to failure of each component (MTTF_c), the duration of each phase during the fault (D_c^p), and the (average) throughput under normal operation (T_n) and during each fault phase (T_c^p). These parameters are affected by scaling in different ways.

**Figure 9:** Unavailability and performability of PRESS on 8 nodes, when (a) scaling analytically from a 4-node configuration in which PRESS has 128 MB of memory on each node; (b) using measurements on 8 nodes, each of which has 64 MB of memory; and (c) using measurements on 8 nodes, each of which has 128 MB of memory.
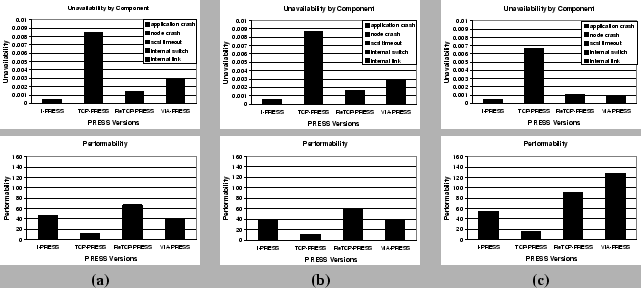$\begin{figure}\begin{center} \begin{tabular}{ccc} \epsfig{file=../figs/scaling/... ...5in}\\ {\bf (a)} & {\bf (b)} & {\bf (c)} \end{tabular}\end{center}\end{figure}$

Let us refer to the MTTF_c in a configuration with N nodes as MTTF_c^N. MTTF_c in a configuration with S times more nodes, MTTF_c^SN, is MTTF_c^N/S. Assuming that the bottleneck resource is the same for the N-node and the SN-node configurations, the durations D_c^p should be the same under both configurations. Further assuming a linear increase in throughput for PRESS (in general, designers using our methodology will need to understand/measure throughput vs. number of nodes for the service under study for scaling), we scale throughput as T_n^SN = S x T_n^N. Unfortunately, the effect of scaling on the throughput of each fault phase is not as straightforward. When the effect of the fault is to bring down a node or make it unaccessible, for instance, the throughput of phase C should approach T_n^SN - T_n^SN/SN under SN nodes, whereas the average throughput of phases B and G should approach (T_n^SN - T_n^SN/SN)/2 and T_n^SN/2 respectively. Just as under N nodes, the throughput of phases A and F should approach 0 under SN nodes.

Finally, an important effect occurs as we scale up, when the cluster-wide cache space almost eliminates accesses to disks. This reduces the impact of disk faults on availability, because the duration of a fault may not overlap with any accesses to cold files.

Figure 9 shows the scaled modeling results using the above rules, as well as results using measurements taken directly on PRESS running on 8-nodes. Observe that our scaling results are very accurate compared to the measured results for 8 nodes, each with 64 MB of memory. This is because the cluster-wide amount of cache memory was kept constant, thus, PRESS still depended on the disk for fetching cold files. However, if each node in the 8-node cluster has 128 MB, then the results are significantly different. Because disk faults no longer impact availability--the working set fits in memory--VIA-PRESS now achieves the best performability. When we eliminate the contribution of disk faults to unavailability in our scaled modeling, we again achieve a close match between modeling and measurements.

In summary, we observe that our methodology produces accurate results when scaling to larger configurations than that available at design/testing time. However, the service designer must understand the system well enough to account for effects of crossing boundaries, where some resource may become more or less critical to system behavior.

Lessons Learned

Applying our 2-phased methodology to PRESS we learned a few lessons. First, we found that the fault-injection phase of our methodology exposed not only implementation bugs, but more importantly conceptual gaps in our reasoning about how the system reacts to faults. For example, an intermittent VIA switch fault created a network of singletons that was incapable of rejoining, even after the switch came back on-line. These experiments demonstrated that some of the faults not originally considered in the PRESS design had a significant impact on the behavior of the server. We also found the second phase of the methodology to be extremely useful for quantitatively reasoning about the impact of design tradeoffs. For example, for all versions except I-PRESS, operator response time is critical to overall performability. While a designer may intuitively understand this, our methodology allows us to quantify the impact of decreasing or increasing operator support.

The second lesson is that runtime fault detection and diagnosis is a difficult issue to address. Consider the heartbeat system implemented in ReTCP-PRESS. What should a loss of heartbeat indicate? Should it indicate a node fault? Does it indicate some failure on the node? How can we differentiate between a node and a communication fault? Should we differentiate between node and application faults? Again, this implies that systems must carefully monitor the status of all its components, as well as have a well-defined reporting system, in which each status indicator has a clearly defined semantic.

Finally, efforts to achieve high availability will only pay off if the assumed fault model matches actual fault scenarios well. Mismatches between PRESS's fault model and actual faults led to some surprising results. A prime example of this is PRESS's assumption that the only possible faults are node or application crashes. This significantly degrades the performability of ReTCP-PRESS and VIA-PRESS because other faults that also led to splintering of the cluster (e.g., link fault) eventually required the intervention of a human operator before full recovery could occur.

One obvious answer to this last problem is to improve PRESS's fault model, which is currently very limited. However, the more complex the fault model, the more complex the detection and recovery code, leading to higher chances for bugs. Further, detection would likely require additional monitoring hardware, leading to higher cost as well. One idea that we have recently explored in [24,26] is to define a limited fault model and then to enforce that fault model during operation of the server. We refer to this approach as Fault Model Enforcement (FME). As an example FME policy, in [24] we enforced the node crash model in PRESS by forcing any fault that leads to the separation of a process/node from the main group to cause the automatic reboot of that node. While this is an extreme example of FME, it does improve the availability of PRESS substantially, as well as reduces the need for operator coverage.

Related Work

There has been extensive work in analyzing faults and how they impact systems [11,31,17]. Studies benchmarking system behavior under fault loads include [15,19]. Unfortunately, these works do not provide a good understanding of how one would estimate overall system availability under a given fault load.

There has also been a large number of system availability studies. Two approaches that are used most often include empirical measurements of actual fault rates [3,13,20,16,23] and a rich set of stochastic process models that describe system dependencies, fault likelihoods over time, and performance [10,21,30]. Compared to these complex stochastic models, our models are much simpler, and thus more accessible to practitioners. This stems from our more limited goal of quantifying performability to compare systems, as opposed to reasoning about system evolution as a function of time.

A recent work [1] proposed that faults are unavoidable and so systems should be built to recover rapidly, in addition to being fault-tolerant. While similar in viewpoint, our proposed methodology concentrates more on evaluating performability independently of the approach taken to improve performance or availability.

Perhaps more similar to our work is that of [6], which outlines a methodology for benchmarking systems' availability. Other works have proposed robustness [29] and reliability benchmarks [34] that quantify the degradation of system performance under faults. Our work here differs from these previous studies in that we focus on cluster-based servers. Our methodology and infrastructure seem to be the first directed to studying these servers, although recent studies have looked at response time and availability of a single-node Apache Web server [18]. Though other previous work proposes availability-improving strategies for applications spanning large configurations [9], we seem to be the first group to quantify the performability and the design and environmental tradeoffs of cluster-based servers.

Finally, we recently used the methodology introduced here to quantify the effects of two different communication architectures on the performability of PRESS [25].

Conclusions

The need for appropriate methodologies and infrastructures for the design and evaluation of highly available servers is rapidly emerging, as availability becomes an increasingly important metric for network services. In this paper, we have introduced a methodology that uses fault-injection and analytical modeling to quantitatively evaluate the performance and availability (performability) of cluster-based services. Designers can use our methodology to study what if scenarios, predicting the performability impact of design changes. We have also introduced Mendosus, a fault-injection and network emulation infrastructure designed to support our methodology.

We evaluated the performability of four different versions of PRESS, a sophisticated cluster-based server, to show how our methodology can be applied. In addition, we also showed how our methodology can be used to assess the potential impact of different design decisions and environmental parameters. An additional benefit of studying the various versions of PRESS is that our results provided insights into server design, particularly concerning runtime fault detection and diagnosis.

Bibliography

About this document ...

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)

The command line arguments were:
latex2html -nonavigation -math -html_version 4.0 -split 0 paper.tex

Using Fault Injection and Modeling to Evaluate the
Performability of Cluster-Based Services¹