Storage Response Time

To determine the performance impact of disk I/O, we must estimate the average response time R_S from storage. We model each storage server as a simple queuing center, parameterized for k disks; to simplify the presentation, we assume that the storage servers in the utility are physically homogeneous. Given a stable request mix, we estimate the utilization of a storage server at a given IOPS request load $\lambda _S$ as $\lambda_S/\mu_S$ , where $\mu_S$ is its saturation throughput in IOPS for that service's file set and workload profile. We determine $\mu_S$ empirically for a given request mix. A well-known response time formula then predicts the average storage response time as:

$\begin{displaymath}R_S = \frac{k/\mu_S}{1-(\lambda_S/\mu_S)} \end{displaymath}$

(3)

**Figure:** Predicted and observed R_S for an NFS server (Dell 4400, k=4 Seagate Cheetah disks, 256MB, BSD/UFS) under three synthetic file access workloads with different fileset sizes.
$\begin{figure} \centerline{\epsfig{file=try1.eps, width=\figwidth}} \end{figure}$

This model does not reflect variations in cache behavior within the storage server, e.g., from changes to M or $\lambda _S$ . Given the heavy-tailed nature of Zipf distributions, Web server miss streams tend to show poor locality when the Web server cache (M) is reasonably provisioned [14].

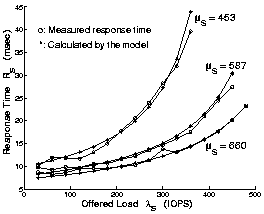
Figure 4 shows that this model closely approximates storage server behavior at typical utilization levels and under low-locality synthetic file access loads (random reads) with three different fileset sizes (T). We used the FreeBSD Concatenated Disk Driver (CCD) to stripe the filesets across k=4 disks, and the fstress tool [2] to generate the workloads and measure R_S.

Since storage servers may be shared, we extend the model to predict R_S when the service receives an allotment $\phi$ of storage server resources, representing the maximum storage throughput in IOPS available to the service within its share.

$\begin{displaymath}R_S = \frac{k/\phi}{1 - (\lambda_S/\phi)} \end{displaymath}$

(4)

This formula assumes that some scheduler enforces proportional shares $\phi/\mu_S$ for storage. Our prototype uses Request Windows [18] to approximate proportional sharing. Other approaches to differentiated scheduling for storage [23,33] are also applicable.