Micah Sherr Matt Blaze Boon Thau Loo
University of Pennsylvania
This paper describes Veracity, a practical fully-decentralized service for securing network coordinate systems. In Veracity, all advertised coordinates and subsequent coordinate updates must be independently verified by a small set of nodes via a voting scheme. Unlike existing approaches, Veracity does not require any a priori secrets or trusted parties, and does not depend on outlier analysis of coordinates based on a fixed set of neighbors. We have implemented Veracity by modifying an open-source network coordinate system, and have demonstrated within a simulated network environment and deployment on PlanetLab that Veracity mitigates attacks for moderate sizes of malicious nodes (up to 30% of the network), even when coalitions of attackers coordinate their attacks. We further show that Veracity resists high levels of churn and incurs only a modest communication overhead.
Decentralized network coordinate systems such as
Vivaldi [7], PIC [6], ICS [19], Big-bang
simulation [29], and NPS [22] have been proposed as a
means of efficiently estimating network distances without having to
explicitly contact the end-hosts involved. Distributed algorithms map
nodes to 
-dimensional coordinates such that the distance between
two nodes' coordinates corresponds to a network distance (e.g.,
latency) between the pair. For a network with 
nodes, coordinate
systems linearize the information necessary to compute pairwise
network distances, allowing nodes to estimate 
distances using
embedded coordinates.
Coordinate systems support a wide range of network services, including proximity-based routing [31], neighbor selection in overlays [9], network-aware overlays [23], and replica placement in content-distribution networks [8,37]. Several large-scale coordinate systems are currently deployed on the Internet. For example, the Vuze client (formally called Azureus) for BitTorrent uses coordinate systems for efficient distributed hash table (DHT) traversal [2] and locality-based neighbor selection [35], and currently operates on more than one million nodes [18].
Unfortunately, the distributed nature of coordinate systems make them particularly vulnerable to insider manipulation. To illustrate, recent studies [16] on Vivaldi have shown that when 30% of nodes lie about their coordinates, Vivaldi's accuracy decreases by a factor of five. When attackers collude, even 5% malicious nodes have a sizable impact on the system's accuracy.
In addition to causing significantly decreased accuracy and performance, corrupted coordinate systems may serve as stepping stones for attacks against the applications that rely on them. Attackers who control the coordinate system may advertise attractive (but false) coordinates for nodes under their control, increasing the likelihood that such hosts will be selected for routes, neighbors, or replicas. Such compromises enable myriad attacks against the overlying services. For example, malicious nodes may misdirect intercepted messages sent via overlay routing, return false data when serving as a replica in a content distribution network, or partition the keyspace in a distributed hash table.
This paper presents Veracity , a fully decentralized service for securing network coordinate systems. Veracity provides a practical deployment path while providing equivalent (or greater) security than previously proposed coordinate security systems. Unlike prior proposals, Veracity does not require either pre-selected trusted nodes [15], the triangle inequality test [6], or outlier detection based on a fixed neighbor set [40], allowing Veracity to be practically deployed and react more rapidly to changes in network conditions. Veracity is also agnostic to the type of decentralized coordinate system being deployed, and can be employed as a protection service over existing decentralized coordinate systems [7,6,19,22].
At a high-level, Veracity utilizes a two-step verification process. The first step involves a majority vote-based scheme in which a published coordinate has to be independently verified by a deterministically assigned set of verification nodes before it is used by peers. An adversary who attempts to disrupt the network by publishing inconsistent coordinates will fail this verification step, and consequently its coordinates will be ignored. As an additional measure, a second verification step utilizes a set of randomly chosen peers to independently compute the estimation error due to a new coordinate, and reject the coordinate if the error is above a threshold. This second protection mechanism detects attacks in which malicious nodes delay responses to measurement probes. The combination of the two techniques ensures that Veracity can tolerate a high fraction of malicious nodes that concurrently report false coordinates and delay latency measurements.
In this paper, we focus our implementation and evaluation on Vivaldi since it is widely used [3] and has been the focus of recent work [15,40] on securing coordinate systems. We demonstrate via execution in a simulated network environment using realistic network traces [38,17] and a deployment on PlanetLab that Veracity mitigates attacks for moderate sizes of malicious nodes (up to 30% of the network), even when coalitions of attackers coordinate their attacks. We further show that Veracity is resistant to high levels of churn and incurs only a modest communication overhead.
Vivaldi uses a fully distributed spring relaxation algorithm, requiring no fixed network infrastructure and no distinguished nodes. The system envisions a spring between each pair of nodes, with the resting position of the spring equaling the network latency between the pair. At any point in time, the distance between the nodes in the coordinate space determines the current length of the spring connecting the nodes.
Nodes adjust their coordinates after collecting published coordinate
and latency measurements from a randomly chosen neighbor. Consider a
node 
that wishes to update its coordinate 
. It picks a
randomly chosen neighbor 
, retrieves its coordinate 
and
performs a round-trip measurement 
from itself to . The
squared error function,
(where
is the distance between their coordinates) denotes the
estimation error between the coordinates of and . Using
Vivaldi's spring relaxation algorithm, 
reflects the potential
energy of the spring connecting the two nodes. Vivaldi attempts to
minimize the potential energies over all springs. In each timestep of
the algorithm, nodes allow themselves to be pulled or pushed by a
connected spring. The system converges when the squared error
function (i.e., the potential energies) is minimized below a
threshold.
Prior studies [16,15] have demonstrated that coordinate systems are susceptible to three classes of attacks: disorder attacks in which malicious insiders attempt to decrease the accuracy of the system by advertising false coordinates and delaying RTT responses, and isolation and repulsion attacks in which the attacker respectively attempts to isolate or repulse a subset of targeted nodes. Veracity's general approach defends against malicious nodes that falsify their coordinates or induce/report artificially inflated latencies. Hence, the techniques described in this paper can mitigate all three attacks.
We adopt the constrained-collusion Byzantine
model proposed by Castro et al. [5] in which malicious nodes
can insert, delete, or delay messages. Given a network of size , and
some fraction (
) of malicious attackers, there exist independent
coalitions of size 
, where
.
To assess the accuracy of a virtual coordinate, we measure the median error ratio of a node 
, defined as the median over the error ratios
and all other nodes 
(
).
Conceptually, Equation 1 computes the difference between
the computed latency between 
and 
based on coordinates
(
) and the actual measured RTT (denoted by
). The accuracy of a node's coordinate increases
inversely with its median error ratio. The use of median provides an
intuitive measure of a coordinate's accuracy and is more robust than
average to the effects of outlier errors. Previous
approaches [7,22,40] define similar metrics.
To gauge the accuracy of the system as a whole, we define the system error ratio as the median over all peers' median error ratios. The system error ratio enables us to quantitatively compare the performance and security of Veracity and Vivaldi. To show lower performance bounds, we also consider the 90th percentile error ratio - i.e., the 90th percentile of nodes' median error ratios.
We first provide an overview of Veracity's security mechanisms. We base our description on Vivaldi's coordinate update model. While other decentralized coordinate systems [6,19,22] differ in their implementations, the update models are conceptually similar to Vivaldi's, and hence, Veracity's techniques are applicable to these systems as well.
To update its coordinate, a participating node (the investigator) periodically obtains the coordinate of a selected peer (the publisher) and measures the RTT between the two nodes. In most implementations, the publisher is typically a pre-assigned neighbor node of the investigator. In Veracity, we relax the requirement that a publisher has to be a fixed neighbor of the investigator and instead use a distributed directory service (Section 4.2) to enable investigators to scalably select random publishers on demand.
The basic update model of Vivaldi leads to two possible avenues of attacks: first, if the publisher is dishonest, it may report inaccurate coordinates. Second, the publisher may delay the RTT probe response to increase the error of the investigator's updated coordinate. To defend against such attacks, Veracity protects the underlying coordinate system through a two-step verification process in which groups of nodes independently verify the correctness of another node's coordinates. We outline these two processes below, with additional details presented in Section 4.
An important benefit of Veracity is that it makes no distinction between intentionally falsified coordinates and those that are inaccurate due to limitations of the coordinate embedding process. In either case, Veracity prevents the use of inaccurate coordinates.
This section presents details of Veracity's two-step verification protocol. We first focus on various mechanisms necessary to realize publisher coordinate verification that prevents investigators from considering inaccurate coordinates. We then motivate and describe the candidate coordinate verification that protects against malicious RTT probe delays by the publisher.
 |
(e.g.,
SHA-1) to its network address. (To prevent malicious peers
from strategically positioning their GUIDs, Veracity restricts allowable
port numbers to a small range.) Given a node with GUID 
, the
members of its VSet are the peers whose GUIDs are closest to
, determined using the recurrence:
ranges from 
to the VSet size, 
. A larger
increases the trustworthiness of coordinates (since more
nodes are required in the verification process) at the expense of
additional communication.
VSet construction utilizes a hash function to increase the difficulty
of stacking VSets with collaborating malicious nodes. Attackers who
control large coalitions of peers may be able to populate a majority
of a particular malicious node's VSet (for example, by strategically
choosing IP addresses within its assigned range), but such VSet
stacking requires at a minimum
peers
per VSet. In practice, many more malicious peers are required since
the attacker does not have complete discretion over the IP addresses
of its coalition members. Moreover, as nodes join and leave the
network, VSet members change (since the nodes whose GUIDs are closest
to
also change), significantly impairing the ability
to persistently stack VSets.
Veracity utilizes a distributed directory service to resolve VSet
members and route messages based on node GUIDs. The directory service
implements a single API function, deliver(
), which delivers
the message 
to the peer whose GUID is closest to according to
a keyspace distance metric. Veracity is compatible with any distributed
directory service that supports the deliver function. We explore
the implementation of distributed directory services in
Section 5.
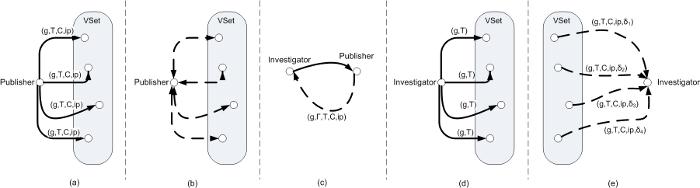
As shown in Figure 1(a), when a publisher updates its
coordinate, it transmits an update tuple
to
members of its VSet using the deliver function provided by the
directory service. The update tuple contains the following values:
is the publisher's GUID, 
is a logical timestamp incremented
whenever the publisher updates his coordinate, 
is the new
coordinate, and 
is the publisher's network address. Upon
receiving the update tuple, each VSet member 
measures the RTT
between itself and (Figure 1(b)), and computes the
error ratio
is 's coordinate and
is the
distance between the coordinates. Finally, locally stores the
evidence tuple
. Nodes
periodically purge tuples that have not recently been queried to
reduce storage costs.
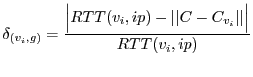
To update its coordinate, the investigator queries a random node (via
a deliver message to a random GUID ) in the network (i.e.,
the publisher). As depicted in Figure 1(c), the
publisher replies with a claim tuple
.
The investigator immediately discards the publisher's coordinates if
the publisher's IP address is not ,
, or it
deems (VSet size) insufficiently large to offer enough
supporting evidence for the coordinate.
Otherwise, the investigator transmits the evidence query
to each member of the publisher's VSet, constructed on
demand given according to Eq. 2
(Figure 1(d)). If a VSet member stores an
evidence tuple containing both and (logical timestamp), it
returns that tuple to the investigator (Figure 1(e)).
The investigator then checks that the GUID, network address, and
coordinates in the publisher's claim tuple matches those in the
evidence tuple. If there is a discrepancy, the evidence tuple is
ignored.
After querying all members of the publisher's VSet, the investigator
counts the number of non-discarded evidence tuples for which
, where
is the
investigator's chosen ratio cutoff parameter. Intuitively, this
parameter gauges the investigator's tolerance of coordinate errors: a
large
permits fast convergence times when all nodes are
honest, but risks increased likelihood of accepting false coordinates.
If the count of passing evidence tuples meets or exceeds the
investigator's evidence cutoff parameter, 
, the coordinate is
considered verified. Otherwise, the publisher's coordinate is
discarded.
To determine an appropriate value for the ratio cutoff parameter
, we examined Vivaldi's system error ratio when run
against the Meridian [38], King [17], and
Scalable Sensing Service (S
) [39] datasets, as well as a
pairwise latency experiment that we executed on
PlanetLab [24] (PL). Simulations and the PlanetLab
experiment used Bamboo [3], a DHT with a Vivaldi
implementation and a simulation mode that takes as input a matrix of
pairwise latencies. Due to scalability limitations, the simulator
used the first 500 nodes from the Meridian and King datasets.
Simulation results were averaged over 10 runs.
Table 1 provides the properties of the four datasets
as well as Vivaldi's achieved system error ratio.
An appropriate value for
should be sufficiently large
to accommodate baseline errors. For example, in our Veracity
implementation (see Section 6.1), we use a ratio
cutoff parameter
of 
, well above the system error
ratio for all datasets.
In the absence of network churn, the VSet membership of a publisher
remains unchanged. With network churn, some of the VSet members may
be modified as the keyspace of the directory service is reassigned.
New VSet members may not have stored any evidence tuples, but as long
as (evidence cutoff parameter) VSet members successfully
verify the coordinate, the coordinate can be used. In our experiments,
we note that even when is 
for a VSet size of 
, Veracity can
tolerate moderate to high degrees of churn while ensuring convergence
in the coordinate system.
 |
The publisher coordinate verification scheme described in Section 4.3 provides the investigator with evidence that a publisher's coordinate is accurate. This does not prevent a malicious publisher from deliberately delaying an investigator's RTT probe, thereby causing the investigator to update its own coordinate erroneously. (Recall that to update its coordinate, the investigator must measure the RTT between itself and the publisher after having obtained the publisher's coordinate.)
Once an investigator has validated the publisher's coordinate, the
candidate coordinate verification scheme compares coordinate
estimation errors among the investigator and a random subset of nodes
(the RSet ) using the investigator's current coordinate (
)
and a new candidate coordinate (
) calculated using the
publisher's verified coordinate and the measured RTT.
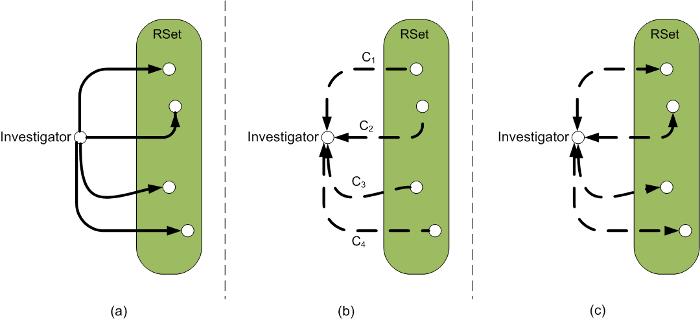
The investigator queries for the coordinates of 
RSet
members by addressing deliver messages to random GUIDs
(Figures 2(a) and 2(b)). As with
(VSet size), a larger (RSet size) increases confidence in
the candidate coordinate at the expense of additional communication.
In our experimentation, we found that setting
provides reasonable security without incurring significant bandwidth
overhead. The investigator (
) measures the RTT between itself and
each RSet member (Figure 2(c)) and computes the average
error ratio
and . If the new coordinate causes the error
ratio to increase by a factor of more than the tolerable error
factor 
, then is discarded and the investigator's
coordinate remains . Otherwise, the investigator sets as
his new coordinate. The value of must be sufficiently large
to permit normal oscillations (e.g., caused by node churn) in the
coordinate system. Setting
enabled Veracity to converge
at approximately the same rate as Vivaldi for all tested topologies
(we investigate Veracity's effect on convergence time in
Section 6.2.2).
Veracity utilizes DHTs to implement its distributed directory service,
which supports the deliver messaging functionality described in
Section 4.1. While one can adopt a centralized or
semi-centralized directory service, a fully-decentralized solution
ensures scalability, allowing Veracity's security mechanisms to be
deployable at Internet scale. DHTs are ideal because they scale
gracefully with network size, requiring 
messages to resolve
a GUID [34,26,25].
While DHTs ensure scalability, they are vulnerable to insider manipulation [36] due to their distributed nature. Malicious nodes can conduct Sybil attacks to increase their influence by registering multiple identities in the network [13], eclipse attacks in which they falsify routing update messages to corrupt honest nodes' routing tables [33], and routing attacks in which they inject spurious responses to messages that cross their paths [5]. Fortunately, well-studied techniques exist that defend DHTs against such attacks [11,10,4,14,5,1]. We describe defenses that are compatible with Veracity's design below.
Sybil attack countermeasures that are compatible with a decentralized
architecture include distributed registration in which registration nodes, computed using iterative hashing of a new
node's IP address, vote on whether the new node can join the system
based on the number of similar requests it has received from the same
IP address [11]. Alternatively, Danezis et al.
propose using bootstrap graphs that capture the relationships
between joining nodes and the nodes through which they join to
construct trust profiles [10]. Finally, Borisov
suggests the use of cryptographic puzzles (e.g., finding a string in
which the last 
bits of a cryptographic hash are zero) to increase
the cost of joining the network [4].
There are also several security techniques that mitigate eclipse and
routing attacks. The S-Chord system proposed by Fiat et al. organizes
the network into swarms based on GUIDs [14].
Lookups are relayed between swarms and are forwarded only if the
lookup was sent from a majority of the members of the previous swarm.
S-Chord is resilient to attacks in which the adversary controls
nodes, where
, 
is the minimum
number of nodes in the network at any time, 
is a tunable
parameter, and the number of honest nodes is less than or equal to
. Castro et al. propose the use of redundant routing in
which queries are sent via diverse paths [5], reaching
the intended recipient if all nodes on at least one path are honest.
Sanchez et al. improve the redundant routing technique in their Cyclone
system [1], showing that 85% of requests were correctly
delivered when attackers controlled 30% of a 1024 node network and
nodes sent messages using 8 redundant paths.
The impact of utilizing the above secure routing techniques is minimal. All of the above approaches operate below the Veracity protocol and do not affect Veracity's operation. Approaches that rely on redundant messaging incur a linear increase in bandwidth overhead, since all deliver messages must be reliably communicated. As we show in Section 6.5.1, Veracity's communication costs (measured using uncompressed messages) are within the tolerances of even dial-up Internet users. A small linear increase in bandwidth can likely be compensated for by using less expensive message formats (our implementation currently uses Java serialization libraries) and data compression.
We argue that the above DHT security techniques are sufficient to
provide the reliability required of Veracity's deliver messaging
functionality. Furthermore, unforeseen attacks that manage to
circumvent such mechanisms have the effect of artificially increasing
the fraction of malicious nodes in the network (since a greater
fraction of messages will be misdirected towards misbehaving nodes),
and such attacks can be compensated for by increasing (the number
of VSet members that must support a publisher's claimed coordinate
for it to be accepted) and (the RSet size).
Finally, to our best knowledge, Veracity is one of the first attempts at directly addressing the problem of secure distributed directory services and secure neighbor selection in the context of coordinate systems. Existing proposals for securing network coordinate systems either rely on a priori trusted nodes [15,28] or utilize decentralized architectures while ignoring the mechanisms used to locate peers [6,40], implicitly assuming in the latter case that the underlying coordinate system provides some distributed techniques to securely populate neighbor sets. Unfortunately, such an assumption does not hold as none of the existing systems (Vivaldi [7], PIC [6], ICS [19], the Big-bang simulation [29], nor NPS [22]) describe mechanisms for ensuring that neighbor selection cannot be influenced by misbehaving nodes. Veracity utilizes the distributed directory service for both neighbor location and VSet resolution, but other coordinate systems that rely on a directory service solely to determine neighbor sets risk significant vulnerability if the neighbor sets are easily populated by malicious nodes.
In this section, we evaluate Veracity's ability to mitigate various forms of attacks in the presence of network churn. We have implemented Veracity by modifying the Vivaldi implementation that is packaged with Bamboo [3], an open-source DHT that is resilient to high levels of node churn [25] and functions either in simulation mode or over an actual network.
Veracity uses Vivaldi as the underlying coordinate system with a
5-dimensional coordinate plane (the recommended configuration in the
Bamboo source code [3]). Each node attempted to update its coordinate every 10 seconds. The
size of VSets and RSets were both fixed at 7 (
).
We used a ratio cutoff parameter
of and an
evidence cutoff parameter of 4. That is, at least 4 of the 7
VSet members had to report error ratios less than for a
coordinate to be verified. The maximum tolerable increase in error
() for the candidate coordinate verification was set to 
.
Our experiments are carried out using Bamboo's simulation mode as well as on PlanetLab. In the simulation mode, we instantiated 500 nodes with pairwise latencies from the Meridian and King datasets. Due to space constraints, simulation results are shown only for the Meridian dataset. Similar conclusions were drawn from the King dataset and are available in the technical report version of this paper [30]. To distribute the burden of bootstrapping peers, a node joins the simulated network every second until all 500 nodes are present. Nodes join via an already joined peer selected uniformly at random.
In our PlanetLab experiments, the 100 participating nodes joined within 3 minutes of the first node. The selected PlanetLab nodes were chosen in a manner to maximize geographic diversity. The simulation and PlanetLab experiments share a common code base, with the exception of the simulator's virtualized network layer.
In Sections 6.2 through 6.4, we present our results in simulation mode in the absence and presence of attackers, followed by an evaluation on PlanetLab in Section 6.5. We focus our evaluation on comparing Vivaldi (with no protection scheme) and Veracity based on the accuracy of the coordinate system, convergence time, ability to handle churn, and communication overhead.
|
|
|
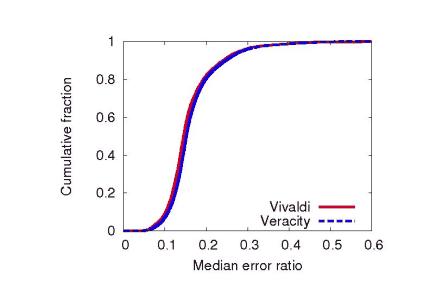
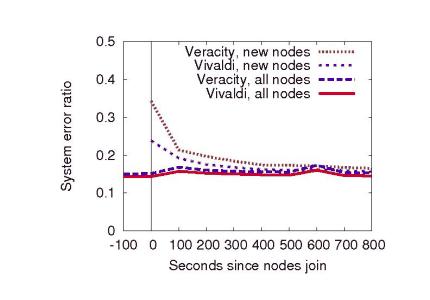
Before evaluating the effectiveness of Veracity at mitigating various attacks, we first provide a performance comparison between Veracity and Vivaldi in the absence of any attackers within the simulation environment.
The polling frequency - the rate at which nodes attempt to update their coordinate - is directly proportional to the system's convergence time. Higher polling frequencies enable faster convergence time at the expense of bandwidth. Although the values of the x-axis can be increased or decreased by adjusting the polling frequency, the shape of the curves remain fixed. Repeating our experiments with smaller and larger polling frequencies produced similar results.
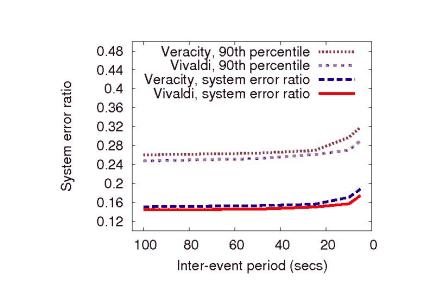
Figure 5 shows the system error ratio for Vivaldi and Veracity for various inter-event periods. Note that the level of churn is inversely proportional to the inter-event period. To illustrate near-worstcase performance, the figure also plots the 90th percentile error ratio.
Both Vivaldi and Veracity are able to tolerate high levels of churn. The
``breaking'' point of both systems occur when the inter-event period
is less than five seconds, reflecting a rate at which approximately a
quarter of the network is replaced every 10 minutes. Churn affects
Veracity since the joining and leaving of nodes may cause the members of a
VSet to more rapidly change, reducing the investigator's ability to
verify a coordinate. Even at this high churn rate, Veracity's system
error ratio (
) is only slightly worse than its error ratio
(
) when there is no churn. It is worth emphasizing that such
high churn (i.e., 25% of the network is replaced every 10 minutes) is
unlikely for real-world deployments. The near 0-slope in
Figure 5 for inter-event periods greater than 10 seconds
shows that neither Vivaldi nor Veracity are significantly affected by more
realistic churn rates.
. Additionally, attackers delay
RTT responses by between 0 and 
ms, choosing uniformly at
random from that range. Malicious nodes immediately begin their
attack upon joining the network.
To emulate realistic network conditions, all simulations experience moderate churn at a median rate of one churn event (a node leaving, immediately followed by a new node joining) every 120 seconds. This churn rate replaces 10% of the nodes during the lifetime of our experiments (100 minutes).
|
Malicious attackers significantly reduce Vivaldi's accuracy, resulting
in a 387% increase in the system error ratio (relative to Vivaldi
when no attack takes place) even when just 10% of nodes are
malicious. When 30% of nodes are malicious, the system error ratio
increases dramatically by 1013%. In contrast, Veracity easily mitigates
such attacks since the coordinate discrepancies are discernible in
evidence tuples, causing inconsistently advertised coordinates to be
immediately discarded by investigators. At low rates of attack
(10%), the system error ratio increases by only 6% (representing a
negligible system-wide median latency error of 
). When 30% of
the network is malicious, Veracity limits the increase in system error
ratio to 32% (
), an 88% improvement over Vivaldi under the
same attack.
Malicious nodes may conduct a more intelligent attack by randomly delaying probes while reporting consistent but erroneous coordinates. That is, each malicious node randomly generates a coordinate and reports the identical (and false) coordinate whenever probed. Such a strategy eliminates coordinate inconsistencies among VSet members. Compared to the previously described attack, this strategy results in lower estimation errors for Vivaldi but does slightly better against Veracity. Here, the increase in Vivaldi's system error ratio is 163% for 10% malicious nodes and 368% for 30% malicious. Veracity successfully defends against heavy network infiltrations, yielding an increase in the system error ratio of just 39% when 30% of the network is malicious. Veracity reaches its tipping point when 40% of nodes are malicious, incurring an increase of 118%. We note that this increase is still far below the 497% increase experienced by Vivaldi.
|
Figure 7 shows Veracity's performance (measured by the cumulative distribution of median error ratios) when the malicious nodes cooperate. For comparison, the Figure also plots the CDFs for equally sized uncoordinated attacks against Veracity and Vivaldi. Since Vivaldi does not collaborate with peers to asses the truthfulness of advertised coordinates, there is no equivalent ``coordinated'' attack against Vivaldi.
For all tested attack strengths, the coordinated attacks did not induce significantly more error than uncoordinated attacks. The resultant system error ratios differed little: when attackers control 30% of the network, the system error ratios are 0.202 and 0.201 for the uncoordinated and coordinated attacks, respectively (for comparison, Vivaldi's system error ratio is 0.679).
 |
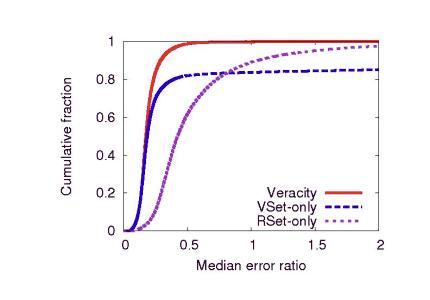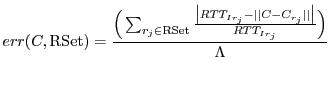
The previous sections show that Veracity's two protections schemes - publisher coordinate verification and candidate coordinate verification - effectively mitigate attacks when the adversary controls a large fraction of the network. In this section, we investigate whether it is sufficient to apply only one of the two techniques to achieve similar security.
Figure 8 shows the cumulative distribution of median error ratios when nodes utilize only publisher coordinate verification (``VSet-only'') or candidate coordinate verification (``RSet-only''). We model the attack scenario from Section 6.3.2 in which 20% of the nodes are malicious and cooperating. For comparison, we also show the CDF when both strategies are utilized (``Veracity''). The VSet-only technique achieves nearly the same system error ratio as Veracity (0.19 and 0.17, respectively). However, using only publisher coordinate verification results in a very long tail of median error ratios. In particular, the 90th percentile error ratio is 0.29 for Veracity and 4.42 for VSet-only. Hence, publisher coordinate verification protects the accuracy of most nodes, but permits a significant degradation in accuracy for a minority of peers.
By itself, candidate coordinate verification results in a higher system error ratio (0.42) than VSet-only or Veracity. Additionally, RSet-only has a longer tail than Veracity, resulting in a 90th percentile error ratio of 1.05 during the attack.
By combining both techniques, Veracity better protects the underlying coordinate system, achieving error ratios that nearly mirror those produced by Vivaldi in the absence of attack (see Figures 6 and 7).
| ||||||||||||||||||||||||||||||||||||||||||||||||
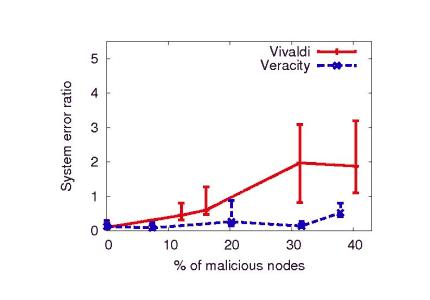
Overall we observe that Veracity is effective at mitigating the effects of disorder attacks. Even under heavy attack (40% malicious nodes), disorder attacks result in a relative system error of 1.54, far below Vivaldi's relative median error of 13.9.
Veracity's effectiveness matches or exceeds that of the prior proposals discussed in Section 7. In contrast to existing coordinate protection systems, Veracity does not require pre-selected trusted nodes, triangle inequality testing, nor outlier detection based on a fixed neighbor set, and is therefore better suited for practical deployment.
 |
While Veracity is intended primarily to defend against disorder attacks,
our next experiment demonstrates the effectiveness of Veracity for
protecting against repulsion and isolation attacks. We carry out a
combined repulsion and isolation attack as follows: malicious nodes
are partitioned into three coalitions, each of which attempts to
repulse and isolate a single victim node. Attackers attempt to
repulse the targeted node towards an extremely negative coordinate
(i.e., having 
in all five dimensions) by using the following
heuristic: if the victim is closer than the attacker to the negative
coordinate, the attacker behaves honestly. Otherwise, the attacker
reports his accurate coordinate but delays the victim investigator's
RTT probe response by 1000ms, causing the victim to migrate his
coordinate (provided it passes candidate coordinate verification)
towards the negative coordinate.
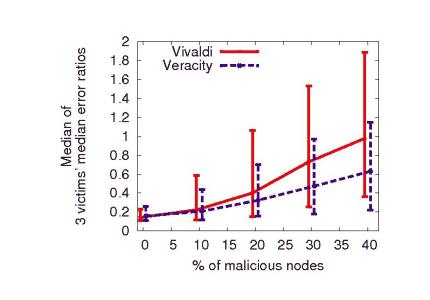
Figure 9 shows the median of the three victim nodes' median error ratios achieved during the combined repulsion and isolation attack. In contrast to previous experiments, we do not use the system error ratio (the median over all peers' median error ratios), as repulsion and isolation attacks target specific victims and need not cause a significant degradation in coordinate accuracy for the remaining peers.
Veracity consistently offers lower median error ratios than Vivaldi. While Veracity does not completely mitigate the effects of repulsion and isolation attacks, our results suggest that the vote-based verification scheme is amenable to defending against such attacks.
In our last experiment, we validate our simulation results by deploying Veracity on the PlanetLab testbed.
|
|
Veracity incurs a communication overhead since publishers' coordinates must
be verified by VSets and investigators' candidate coordinates must be
assessed by RSets. Since Veracity uses a DHT as its directory service, it
leverages the scalability of DHTs: each verification step requires
, where and denotes the
VSet and RSet sizes respectively.
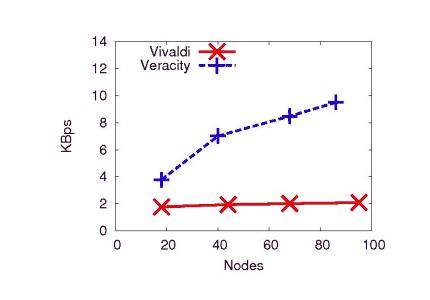
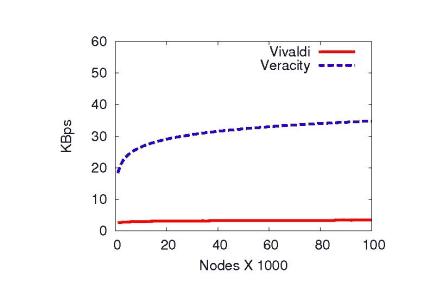
Based on the PlanetLab measurements, we performed logarithmic
regression analysis to extrapolate the per-node bandwidth requirements
of Veracity as the number of nodes increases:
KBps
(
) for Vivaldi and
KBps
(
) for Veracity. Figure 11 shows the
extrapolated bandwidth utilization of Vivaldi and Veracity for large
networks. For a large network consisting of 100,000 nodes, Veracity's
expected per-node bandwidth requirement is a modest 35KBps, making it
accessible to typical broadband users.
 |
PIC detects dishonest nodes by observing that falsified coordinates or delayed measurements likely induce triangle inequality violations (TIVs) [6]. To verify peers' coordinates and measurements, honest nodes use distances to trusted landmarks to detect TIVs. Using a generated transit-stub topology of 2000 nodes, PIC is able to tolerate attacks when up to 20% of the network was controlled by colluding adversaries [6]. However, more recent work has indicated that TIVs can potentially be common and persistent [20], reducing the practicality of PIC's protection scheme on real-world networks.
Kaafar et al. propose the use of trusted surveyor nodes to detect malicious behavior [15]. Surveyor nodes position themselves in the coordinate space using only other trusted surveyors. Nodes profile surveyors to model honest behavior, detecting falsified coordinates and measurements as behavior that differs from their constructed model. Kaafar et al. conclude that their approach is effective when 30% or less of the network is controlled by malicious and cooperating nodes [15]. Their technique requires 8% of the nodes to be a priori trusted surveyors [15] - a nontrivial fraction when the network consists of 100,000 or more nodes.
The RVivaldi system proposed by Saucez et al. protect coordinate systems using surveyors as well as centralized Reputation Computation Agents (RCAs), the latter of which assigns reputations (trust profiles) to coordinates [28,27]. Their technique is evaluated only against non-cooperating adversaries, and tolerates up to 20% malicious nodes [28].
Like Veracity, the system proposed by Zage and Nita-Rotaru is fully distributed and designed for potentially wide-scale deployments [40]. Their approach relies on outlier detection, reducing the influence of nodes whose coordinates are too distant (spatial locality) or whose values change too rapidly in short periods of time (temporal locality). Their technique successfully mitigates attacks when 30% or fewer of the nodes are under an attacker's control [40]. However, the temporal locality heuristic requires that each node maintains an immutable neighborset, a list of neighbors that a node uses to update its coordinates. Wide-scale deployments involving hundreds of thousands of nodes are likely to be dynamic with nodes frequently joining and leaving the system. The high rate of churn will lessen the opportunities for temporal analysis as nodes leave the system (since less history is available), and cause errors in such analysis for newly joined nodes for which frequent changes in coordinates are expected. In contrast, Veracity does not discriminate against spatial or temporal outliers, and as described in Section 6.2.3, tolerates high levels of churn.
This paper extends our original position paper [32] that outlines our initial design of Veracity. This paper additionally proposes a second verification step geared towards ensuring the correctness of coordinate updates in the presence of malicious delays in latency measurements. This paper further presents a full-fledged implementation that is experimented within a network simulation environment and on PlanetLab.
This paper proposes Veracity , a fully distributed service for securing network coordinates. We have demonstrated through extensive network simulations on real pairwise latency datasets as well as PlanetLab experiments that Veracity effectively mitigates various forms of attack. For instance, Veracity reduces Vivaldi's system error ratio by 88% when 30% of the network misbehaves by advertising inconsistent coordinates and adding artificial delay to RTT measurements. Veracity performs well even against cooperating attackers, reducing Vivaldi's system error ratio by 70% when 30% of the network is corrupt and coordinates its attacks.
We argue that Veracity provides a more practical path to deployment while providing equivalent (or greater) security than previously proposed coordinate security systems. Unlike PIC, Veracity does not associate triangle-inequality violations (TIVs) with malicious behavior [6], and as indicated by our simulation and PlanetLab results, does not impose additional inaccuracies in the coordinate system when TIVs do exist. Veracity is fully decentralized, requiring no a priori shared secrets or trusted nodes. In comparison to techniques that require specialized trusted nodes [28,27,15], Veracity is well-suited for applications for which centralized trust models are incompatible (e.g., anonymity networks [31]), and in general, removes central points of trust that may serve as focal points of attack. Veracity's use of distributed directory services enables graceful scalability, and hence the system can easily be applied to wide-scale virtual coordinate system deployments.
Our most immediate future work entails the use of secure network coordinate systems to permit applications to intelligently form routes that meet specific latency and bandwidth requirements. We are also investigating anonymity services [31] that may leverage Veracity to produce high-performance anonymous paths. Finally, we expect to release an open-source implementation of Veracity in the near future.
The authors are grateful to our shepherd, Kenneth Yocum, for his insightful comments and advice. We also thank the anonymous reviewers for their many helpful suggestions. This work is partially supported by NSF Grants CNS-0831376, CNS-0524047, CNS-0627579, and NeTS-0721845.
: A Scalable Sensing Service for Monitoring Large Networked
Systems.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation veracity.tex
The translation was initiated by Micah Sherr on 2009-04-22
