Binny S. Gill
IBM Almaden Research Center
Michael Ko
IBM Almaden Research Center
Biplob Debnath
University of Minnesota
Wendy Belluomini
IBM Almaden Research Center
Non-volatile write-back caches enable storage controllers to provide quick write response times by hiding the latency of the disks. Managing a write cache well is critical to the performance of storage controllers. Over two decades, various algorithms have been proposed, including the most popular, LRW, CSCAN, and WOW. While LRW leverages temporal locality in the workload, and CSCAN creates spatial locality in the destages, WOW combines the benefits of both temporal and spatial localities in a unified ordering for destages. However, there remains an equally important aspect of write caching to be considered, namely, the rate of destages. For the best performance, it is important to destage at a steady rate while making sure that the write cache is not under-utilized or over-committed. Most algorithms have not seriously considered this problem, and as a consequence, forgo a significant portion of the performance gains that can be achieved.
We propose a simple and adaptive algorithm, STOW, which not only exploits both spatial and temporal localities in a new order of destages, but also facilitates and controls the rate of destages effectively. Further, STOW partitions the write cache into a sequential queue and a random queue, and dynamically and continuously adapts their relative sizes. Treating the two kinds of writes separately provides for better destage rate control, resistance to one-time sequential requests polluting the cache, and a workload-responsive write caching policy.
STOW represents a leap ahead of all previously proposed write cache
management algorithms. As anecdotal evidence, with a write cache of 
K pages,
serving a 
+P RAID-
array, using an SPC-1 Like Benchmark, STOW outperforms WOW by
%, CSCAN by 
%, and LRW by 
%, in terms of measured throughput.
STOW consistently provides much
higher throughputs coupled with lower response times across
a wide range of cache sizes, workloads, and experimental configurations.
In spite of the recent slowdown in processor frequency scaling due to power and density issues, the advent of multi-core technology has enabled processors to continue their relentless increase in I/O rate to storage systems. In contrast, the electro-mechanical disks have not been able to keep up with a comparable improvement in access times. As this schism between disk and processor speeds widens, caching is attracting significant interest.
Enterprise storage controllers use caching as a fundamental technique to hide I/O latency. This is done by using fast but relatively expensive random access memory to hold data belonging to slow but relatively inexpensive disks.
Over a period of four decades, a large number of read cache management algorithms have been devised, including Least Recently Used (LRU), Frequency-Based Replacement (FBR) [19], Least Frequently Recently Used (LFRU) [15], Low Inter-Reference Recency Set (LIRS) [13], Multi-Queue (MQ) [24], Adaptive Replacement Cache (ARC) [17], CLOCK with Adaptive Replacement (CAR) [2], Sequential Prefetching in Adaptive Replacement Cache (SARC) [8], etc. While, the concept of a write cache has been around for over two decades, we realize that it is a more complex and less studied problem. We focus this paper on furthering our understanding of write caches and improving significantly on the state of the art.
A write-back (or fast-write) cache relies on fast, non-volatile storage to hide latency of disk writes. It can contribute to performance in five ways. It can (i) harness temporal locality, thereby reducing the number of pages that have to be destaged to disks; (ii) leverage spatial locality, by reordering the destages in the most disk-friendly order, thereby reducing the average cost of destages; (iii) absorb write bursts from applications by maintaining a steady and reasonable amount of free space, thereby guaranteeing a low response time for writes; (iv) distribute the write load evenly over time to minimize the impact to concurrent reads; and (v) serve read hits that occur within the write cache.
There are two critical decisions regarding destaging in write caching: the destage order and the destage rate. The destage order deals with leveraging temporal and spatial localities, while the destage rate deals with guaranteeing free space and destaging at a smooth rate. Write caching has so far been treated mainly as an eviction problem, with most algorithms focusing only on the destage order. The most powerful write caching algorithms will arise when we explore the class of algorithms that simultaneously optimize for both the destage order and the destage rate.
Firstly, we present a detailed analysis of the problem of managing the destage rate in a write cache. While this has remained a relatively unexplored area of research, we demonstrate that it is an extremely important aspect of write caching with the potential of significant gains if done right. Further, we show that to manage the destage rate well, we actually need a new destaging order.
Secondly, we present a Spatially and Temporally Optimized Write caching
algorithm (STOW), that for the
first time, exploits not only temporal and spatial localities, but also manages
both the destage rate and destage order effectively in a single powerful
algorithm that handsomely beats popular algorithms like WOW, CSCAN, and LRW,
across a wide range of experimental scenarios. Anecdotally,
with a write cache of K pages (and high destage thresholds), serving a RAID-5 array,
the measured throughput for STOW at 
ms response time,
outperform WOW by %, CSCAN by %, and LRW by %. STOW consistently
and significantly outperforms all other algorithms across a wide range of cache
sizes, workload intensities, destage threshold choices, and backend RAID configurations.
Although an extensive amount of work has been done in the area of read caching, not all techniques are directly applicable to write caching. While read caching is essentially a two dimensional optimization problem (maximizing hit ratio and minimizing prefetch wastage), write caching is a five dimensional optimization problem (as explained in Section 1.1).
In a write-back cache, the response time for a write is small if there is space in the write cache to store the new data. The data in the write cache is destaged to disks periodically, indirectly affecting any concurrent reads by increasing their average service response time. To reduce the number of destages from the write cache to the disks, it is important to leverage temporal locality and, just like in read caches, maximize the hit (overwrite) ratio. The primary way to maximize temporal locality is to attempt to evict the least recently written (LRW) pages from the cache. An efficient approximation of this is available in the CLOCK [5] algorithm which is widely used in operating systems and databases. These algorithms, however, do not account for the spatial locality factor in write cache performance.
Orthogonally, the order of destages can be chosen so as to minimize the average cost of each destage. This is achieved by destaging data that are physically proximate on the disks. Such spatial locality maximization has been studied mostly in the context of disk scheduling algorithms, such as shortest seek time first (SSTF) [6], SCAN [6], cyclical SCAN (CSCAN) [20], LOOK [18], VSCAN [7], and FSCAN [4]. Some of these require knowledge of the current state of the disk head [12,21], which is either not available or too cumbersome to track in the larger context of storage controllers. Others, such as CSCAN, order the destages by logical block address (LBA) and do not rely on knowing the internal state of the disk.
In the first attempt to combine spatial and temporal locality in write caching for storage systems [10], a combination of LRW [1,3,11] and LST [10,22] was used to balance spatial and temporal locality. This work had the drawback that it only dealt with one disk and it did not adapt to the workload.
In general, the order of destages is different for leveraging temporal locality
versus spatial locality. One notable write caching algorithm, Wise Ordering
for Writes (WOW) [9], removed this apparent contradiction, by combining
the strength of CLOCK [5] in exploiting temporal locality and Cyclical
SCAN (CSCAN) [20] in exploiting spatial locality. As shown in
Figure 1, WOW groups the pages in the cache in terms of write groups
and sorts them in their LBA order. To remember if a write group was recently
used, a recency bit is maintained in each write group. When a page is written in a write group
already present in the cache, the recency bit of the write group is set to 
.
Destages are done in the sorted order of the write groups. However, if the
recency bit of a write group is , the write group is bypassed after
resetting the recency bit to 
.
While WOW solves the destage order problem, the destage rate problem has attracted little research. Both WOW and an earlier work on destage algorithms [23] use a linear thresholding scheme that grows the rate of destages linearly as the number of modified pages in the cache grows. While this scheme is quite robust, destage orders like WOW and CSCAN cannot achieve their full potential due to a destructive interaction between the destage rate and the destage order policies. We are unaware of any research that studies the interaction between the two vital aspects of write caching: the destage order and the destage rate.
Table 1 shows how the set of algorithms discussed above compare. LRW considers only recency (temporal locality), CSCAN considers only spatial locality, and WOW considers both spatial and temporal locality. Our algorithm, STOW (Spatially and Temporally Optimized Writes), tracks spatial and temporal localities, and is scan resistant because it shields useful random data from being pushed out due to the influx of large amounts sequential data. STOW also avoids large fluctuations in the destage rate and cache occupancy.
Historically caching has always been treated as an eviction problem. While it might be true for demand-paging read caches, it is only partially true for write caches. The rate of eviction or the destage rate has attracted little research so far. In this section we explore why the destage rate is a crucial aspect of any good write caching algorithm.
Rather than simply present our approach, we explain why we reject other seemingly reasonable approaches, some of which have been used in the past.
 |
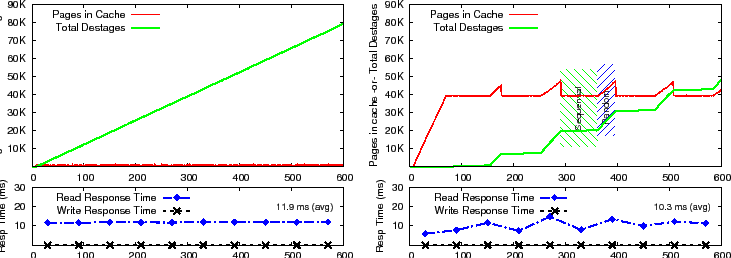The Spikes: Any write caching algorithm destages writes in a particular order. If the workload is such that the algorithm destages sequential data for some time followed by random data, such peaks are inevitable because destaging random data is far more time consuming and during such intervals, the cache occupancy can spike even for steady workloads. With WOW or CSCAN, such spikes appear when the workload has a sequential and a random component that target different portions of the LBA space. This is commonly observed in both real-life and benchmark workloads.
 |
In the WOW [9] paper, a linear threshold scheme is
proposed which is better than the fixed threshold scheme
because it provides a gradual gradation of destage rates which
is more friendly to concurrent reads and also allows the thresholds to be safely
closer to the 100% mark. For example, instead of destaging at full
force after reaching 60% occupancy, linear threshold would use a
number of concurrent destage requests that is proportional to
how close the write cache is to a high threshold (say 80% occupancy).
Beyond the high threshold
it will destage at the full rate. This is the best scheme so far
that we are aware of, however, it cannot address the spike
problem, as evidenced in Figure 3.
In this paper we use an 
notation for the thresholds:
e.g. 
implies that the high threshold is at 
% of the cache
and the low threshold is at 
%.
The STOW algorithm uses two WOW-like sorted circular queues for housing random and sequential data separately. The relative sizes of the queues is continuously adapted according to workload to maximize performance. The decisions for: which queue to destage from, when to destage, and at what rate, are carefully managed to leverage spatial and temporal locality in the workload, as well as to maintain steady cache occupancy levels and destage rates. Despite its simplicity, STOW represents the most comprehensive and powerful algorithm for write cache management.
A write hit (over-write) on a page generally implies that the page and its neighbors are likely to be accessed again. In the context of a storage controller connected to a RAID controller, we would like to postpone the destage of such pages hoping to absorb further writes, thereby reducing the destage load on the disks.
In RAID, each participating disk contributes one strip (e.g. 64 KB) towards each RAID stripe. A RAID stripe consists of logically contiguous strips, one from each data disk. Destaging two distinct pages in the same RAID stripe together is easier than destaging them separately, because in the former case the parity strip needs to be updated only once. We say a stripe hit has occurred when a new page is written in a RAID stripe that already has a member in the write cache. In RAID 5, therefore, a stripe hit saves two disk operations (the read and write of the parity strip), while a hit on a page saves four.
While we divide the write cache in pages of 4KB each, we manage the data structures in terms of write groups, where a write group is defined as a collection of a fixed number (one or more) of logically consecutive RAID stripes. In this paper, we define the write group to be equal to a RAID stripe. We say a write group is present in the cache if at least one of its member pages is physically present in the cache. Managing the cache in terms of such write groups allows us to better exploit both temporal locality by saving repeated destages and spatial locality by issuing writes in the same write group together, thus minimizing parity updates.
Sequential data, by definition, has high spatial locality,
and appears in large clumps in the sorted LBA space
for algorithms such as WOW or CSCAN. In between clumps of sequential data
are random data.
We discovered that destaging random data, even when it is sorted,
is far more time consuming than destaging sequential data.
Therefore, when the destage pointer is in an area full of random data, the slower destage rate
causes the cache occupancy to go up. These
spikes in the cache occupancy could lead to full-cache conditions even for
steady workloads, severely impacting the cache performance. Further, during a spike, a cache is
especially vulnerable to reaching the 
% occupancy mark even with smaller write
bursts.
This discovery led us to
partition the cache directory in STOW into two separate queues RanQ
and SeqQ for the ``random" and the ``sequential" components of a workload. It is
easy to determine whether a write is sequential by looking for the
presence of earlier pages in the cache [8] and keeping a counter.
The first few pages of a sequential stream are treated as random.
If a page is deemed to belong to a sequential stream it is populated in SeqQ;
otherwise, the page is stored in RanQ.
Separating sequential data from random data is a necessary first step towards alleviating the problem caused by the spikes in the cache occupancy. However, this is not sufficient by itself, as we will learn in Section 4.3.4 when we discuss destaging.
The STOW cache management policy is depicted in Algorithm 1. In each queue, RanQ or SeqQ, the write groups are arranged in an ascending order of logical block addresses (LBA), forming a circular queue, much like WOW, as shown in Figure 4. A destage pointer (akin to a clock arm) in each queue, points to the next write group in the queue to be considered for destaging to disk. Upon a page miss (a write that is not an over-write), if the write group does not exist in either queue, the write group with the new page is inserted in the correct sorted order in either RanQ or SeqQ depending on whether the page is determined to be a random or a sequential page. If the write group already exists, then the new page is inserted in the existing write group.
The LBA ordering in both queues allows us to minimize the cost of a destage which depends on how far the disk head would have to seek to complete an operation. The write groups, on the other hand, allow us to exploit any spatio-temporal locality in the workload, wherein a write on one page in a write group suggests an imminent write to another page within the same write group. Not only do we save on parity updates, but we also have the opportunity to coalesce consecutive pages together into the same write operation.
When either RanQ or SeqQ is empty, because the workload lacks the random or the sequential component, then STOW converges to WOW, and by the same token, is better than CSCAN and LRU.
The destage pointer traverses the sorted circular queue looking for destage victims.
Write groups with a recency bit of are skipped after resetting the recency bit
to .
If the recency bit of the write group was found to be ,
then the pages present in the write group are destaged.
Thus, write groups with a recency bit of one get an extra life equal to the time it takes for the
destage pointer to go around the clock once.
Setting the recency bit in RanQ: When a new write group is created in RanQ, the recency bit is
set to (line 24 in Algorithm 1). On a subsequent page hit or a write group hit, the recency bit is set
to (line 9),
giving all present members of the write group a longer life in the cache,
during which they can exploit any overwrites of the present pages or accumulate new
neighboring pages in the same write group. This leads to enhanced hit ratio,
fewer parity updates, and coalesced writes reducing the total number of
destages.
Setting the recency bit in SeqQ:
Whenever a page is written to SeqQ, the recency bit in the corresponding
write group is set to (lines 9 and 20). This is because we anticipate that subsequent pages
will soon be written to the write group by the sequential stream.
Destaging to disk is more efficient if the whole write
group is present since this avoids the extra read-modify-write of the parity
group in a RAID-5 configuration and also coalesces consecutive pages into the same
disk IO if possible.
However, if the page written is the last page of the write group
then the recency bit is forced to (lines 7 and 18). Since the last page of the write group has been
written, we do not anticipate any further writes and can free up the
cache space the next time the destage pointer visits this write group.
 |
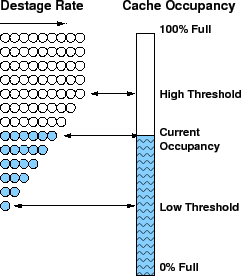In STOW, we use a linear threshold scheme (see Figure 5, as
described in WOW[9])
to determine when and at what rate to destage.
We set a low threshold and a high threshold for the cache occupancy. When the
cache occupancy is below the low threshold, we leave the write data in the
cache in order to gather potential write hits. When the cache occupancy is
above the high threshold, we destage data to disks at the full rate in
order to avoid the full-cache condition which is detrimental to response
time. When the cache occupancy is between the low and high threshold, the
number of concurrent destage requests is linearly proportional to how
close we are to the high threshold. Note, a higher number of concurrent destage
requests to the disks results in a higher throughput for destages, but of course
at the cost of making the disks busier and the concurrent reads slower.
The maximum number of concurrent destage requests (queue depth) is set to a
reasonable [9] in our experiments.
Once we have decided to destage from a queue, we should stick with that decision for a reasonable amount of time, so as to minimize the spatial locality pollution caused by the mixing of two sorted orders. To realize this, we define a fixed number called the HysteresisCount. Once a decision has been made to destage from a particular queue, we continue destaging from the same queue until, (i) we have destaged HysteresisCount pages from the queue; or (ii) either queue has since grown by more than HysteresisCount pages. Note that destages from RanQ are slower and the second condition avoids a large buildup in SeqQ in the meantime. Once either condition is met, we reevaluate which queue to destage from.
Normally, we fix HysteresisCount to be equal to 
times the number
of spindles in the RAID array. This ensures that a reasonable number of destage
operations are performed in one queue's sorted order, before moving to the other queue's
sorted order.
However, we observed that fluctuations in the cache occupancy are proportional to the HysteresisCount. To maintain a smooth destage rate these fluctuations need to
be small relative to the difference between the high and low thresholds.
Therefore, we limit HysteresisCount to
be no more than 
th of the difference (in terms of pages) between the
thresholds.
As we stated earlier, we use the size of SeqQ relative to DesiredSeqQSize for determining which queue to destage from, every time we have destaged HysteresisCount pages. Therefore, we need to wisely and continuously adapt DesiredSeqQSize to be responsive to the workload so as to maximize the aggregate utility of the cache. The marginal utility, in terms of IOPS gained, of increasing the size of either RanQ or SeqQ, is not well understood. Therefore, we propose intuitive heuristics that are very simple to calculate and result in good performance.
Marginal utility for RanQ: We would like to estimate the extra IOs
incurred if we make RanQ smaller by unit cache size (a page).
We first approximate
the number of misses that would be incurred if we reduce the size of RanQ.
Let 
be the hit rate for first time hits in RanQ (where the recency bit is previously zero).
We consider only page hits for RAID-10 but any stripe hit for RAID-5, since
in RAID-5, stripe hits save parity updates (two IOs) and are more common than page hits.
Assuming a uniform distribution of these hits, we can compute the density
of hits to be 
.
Since a cache does have diminishing returns as its size grows, we
add a factor of 
(empirically determined). Each extra miss results in two
extra IOs to the disk, yielding a marginal utility of .
Marginal utility for SeqQ: We would like to estimate the extra IOs
incurred by making SeqQ smaller by unit cache size.
We first measure the rate, 
, at which there
are breaks in the logical write group addresses being destaged from SeqQ.
Each contiguous group of pages destaged is called a stretch.
The smaller the size of SeqQ, the higher is the rate . Since
is inversely proportional to the cache size, the marginal increase in
equal to 
(since 
= const,
).
Each extra break in SeqQ results in one extra write to all 
disks.
This yields a marigical utility of 
.
We adapt the sizes of RanQ and SeqQ targeting a condition
where
, to minimize the IOs to the disk, maximizing
the performance of the cache.
We implement the above in Algorithm 3 as follows:
Initialization: The initial value of DesiredSeqQSize is the size of SeqQ when the write cache first reaches the low threshold of destaging.
Decrement: DesiredSeqQSize is reduced by one if: We have a hit (page hit for RAID-10 and write group hit for RAID-5) in RanQ (line 2), where the recency bit is zero (line 3), and the DesiredSeqQSize is not already HysteresisCount lower than the current SeqQ size (line 4).
Increment: DesiredSeqQSize is incremented whenever there is break
in the logical addresses of the write groups in SeqQ
being destaged (line 11). The amount
incremented is
, where is the number of disks in the
RAID array.
There are two conditions when we
do not increment DesiredSeqQSize: (i) When the break in the logical
address occurred after a relatively long stretch (more than what the queue depth
allows to be destaged together) (line 12);
or (ii) RanQ is already below its rightful share of the cache
based on the proportion of random requests in the workload (line 13).
A schematic diagram of the experimental system is depicted in Figure 6.
We use an IBM xSeries 3650 machine equipped with two Intel Xeon 3 GHz processors, 4 GB DDR2 memory at 667 MHz, and eight 2.5" 10K RPM SAS disks (IBM 40K1052, 4.5 ms avg. seek time) of 73.4 GB each. A Linux kernel (version 2.6.23) runs on this machine to host all our applications and standard workload generators. We employ five SAS disks for our experiments, and one for the operating system, our software, and workloads.
We study two popular RAID configurations, viz. RAID-5 and RAID-10, using Linux Software RAID. We issue direct I/O to the virtual RAID disk device, always bypassing the kernel buffer. For RAID-5, we use 5 SAS disks to create an array consisting of 4 data disks and 1 parity disk. We choose the strip size for each disk to be 64 KB, with the resulting stripe group size being 256 KB. For RAID-10, we use 4 SAS disks to create an array in a 2 + 2 configuration. We use the same strip size of 64 KB for each disk.
We use the entire available storage in one configuration which we call the Full Backend. For RAID-5, with the storage capacity of four disks, Full Backend amounts to 573 million 512-byte sectors. For RAID-10, with the storage capacity of two disks, Full Backend amounts to 286 million 512-byte sectors. We also define a Partial Backend configuration, where we use only 1/100th of the available storage. While Full Backend is characterized by large disk seeks and low hit ratio, the Partial Backend generates only short seeks coupled with high hit ratios.
For simplicity, we use volatile DDR2 memory as our write cache. In a real life storage controller, the write cache is necessarily non-volatile (e.g. battery-backed). In our setup, the write cache is managed outside the kernel so that its size can be easily varied allowing us to benchmark a wide range of write cache sizes.
We do not use a separate read cache in our experiments for the following reason. Read misses disrupt the sequentiality of destages determined by any write caching algorithm. A read cache reduces the read misses and amplifies the gains of the better write caching algorithm. Therefore the most adverse environment for a write caching algorithm is when there is no read cache. This maximizes the number of read misses that the disks have to service concurrent to the writes and provides the most valuable comparison of write caching algorithms.
Nevertheless, we do service read hits from the write cache for consistency.
SPC-1 [16,14] is the most respected performance benchmark in the storage industry. The benchmark simulates real world environments in a typical server class computer system by presenting a set of I/O operations that are typical for business critical applications like OLTP systems, database systems and mail server applications. We use a prototype implementation of the SPC-1 benchmark that we refer to as SPC-1 Like.
The SPC-1 workload roughly consists of 40% read requests and 60% write requests. For each request, there is a 40% chance that the request is sequential and a 60% chance that the request is random with some temporal locality. SPC-1 scales the footprint of the workload based on the amount of storage space specified. Therefore for a given cache size, the number of read and write hits will be larger if the backend is smaller (Partial Backend), and smaller if the amount of storage exposed to the benchmark is larger (Full Backend).
SPC-1 assumes three disjoint application storage units (ASU). ASU-1 is assigned 45% of the available back-end storage and represents ``Data Store". ASU-2 is assigned 45% and represents ``User Store". The remaining 10% is assigned to ASU-3 and represents ``Log/Sequential Write". In all configurations, we lay out ASU-3 at the outer rim of the disks followed by ASU-1 and ASU-2.
 |
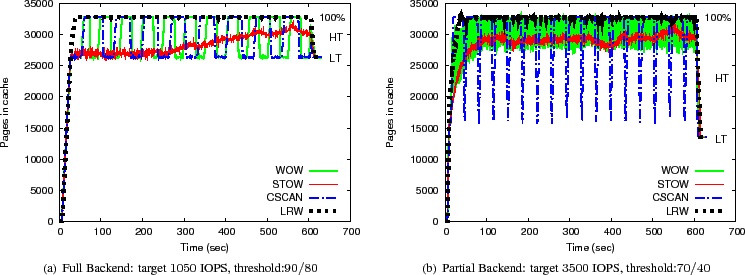We compare the performance of LRW, CSCAN, WOW and STOW under a wide range of cache size, workload, and backend configurations. We use linear thresholding to determine the rate of destages for all algorithms.
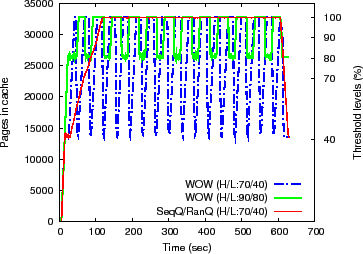
In Figure 7(a),
we observe that the occupancy graph for
WOW as well as CSCAN fluctuates wildly between the low threshold and the
% occupancy level.
For the same scenario, LRW's cache occupancy remains at % occupancy,
which implies that most of the time it does not have space
for new writes.
Only STOW exhibits measured changes in the overall
cache occupancy, consistently staying away from the full-cache condition.
Note that with linear thresholding,
the destage rate is a function of the cache occupancy, and consequently,
large fluctuations are detrimental to performance.
The sequential writes in the SPC-1 benchmark are huddled in a small fraction of the address space. As the destage pointer in WOW or CSCAN moves past this sequential region and into the subsequent random region, the occupancy graph spikes upwards because the cache cannot keep up with the incoming rate while destaging in the random region. This disparity can be so large that even the maximum destage concurrency may not be sufficient to keep up with the incoming rate, leading to the dreaded full-cache condition (Figure 7(a)).
Also note the flat bottoms at the low threshold on the occupancy graphs for WOW and CSCAN in Figure 7(a). Since destaging sequential data is quick and easy, the cache occupancy quickly drops down close to the low threshold, where it uses only a small portion of the allowed destage queue depth to keep up with the incoming rate of the overall workload. The lackadaisical destage rate in the sequential region results in underutilization of disks which is ironic given that the disks cannot keep up with the incoming rate when destages move to the subsequent random regions.
STOW wisely alternates between the two types of destages, ensuring that the disks are continuously utilized at a relatively constant rate. This eliminates large fluctuations in the occupancy curve for STOW in both the full and partial backend cases.
![\begin{figure*}\centerline{
\subfigure[Full Backend: RAID 5]{
\epsfig{figure=f...
...figure=figs/part_Pvary_C32768_T1030_RAID10.eps, scale=0.65}
}
}
\end{figure*}](img46.png) |
Presenting meaningful results: We use the best way to present
results for write caching improvements: the throughput-response time curve.
We present gains in terms of bandwidth
improvements at the same (reasonable) response time. Another approach is
to present gains in terms of response times at the same throughput.
E.g., at 
IOPS in Figure 8(a), we could report at least
a 
x improvement in response time over the contenders.
While it is accurate, we believe, it is not as informative because it can be
cherry-picked to aggrandize even modest gains in such ``hockey-stick" plots.
Backward bending: We also observe the backward bending phenomenon in some curves which happens whenever a storage controller is overdriven [9]. In this regime, congestion caused by the increasing queue lengths, lock contention, and CPU consumption, bogs down a storage controller such that the disks no longer remain the bottleneck.
In the top panel of Figure 8, we compare the average response time (aggregate read and write) as a function of the throughput achieved when the target throughput is gradually increased in the SPC1-Like workload generator. Overall, STOW outperforms all algorithms significantly across all load levels. Observe that WOW and CSCAN improve as the threshold range becomes wider since a wider range allow them to contain the fluctuations better, hitting the full-cache condition for lesser amount of time. Since there are no large fluctuations in STOW's cache occupancy, STOW delivers a consistent performance with any threshold, beating the best configuration for either WOW or CSCAN.
In particular, at around ms response time, with a threshold of ,
in terms of SPC-1 Like IOPS in RAID-5,
STOW outperforms WOW by %, CSCAN by %, and LRW by %. With a threshold
of 
, STOW beats WOW by 
%, CSCAN by 
%, and LRW by %.
Similarly, in RAID-10 with a threshold,
STOW outperforms WOW by 
%, CSCAN by 
%, and LRW by 
%, while, with a threshold
of , STOW beats WOW by %, and CSCAN and LRW by %.
These gains are not trivial in the world of hard drives which sees only a
meager improvement rate of 
% per year.
Although we include data points at response times greater than 
ms, they are
not of much practical significance as applications would become very slow at
those speeds. Even the SPC-1 Benchmark disallows submissions with greater than
ms response times.
For the partial backend scenario, depicted in the lower panel in Figure 8,
we use only the outer 1/100th of each disk in the RAID array, creating
a high hit ratio scenario with short-stroking on the disks. In this setup, the
fluctuations in the occupancy for WOW are closer together
(Figure 7(b)), resulting in a more rapid alternation between
sequential and random destages. This helps WOW somewhat, however, in terms of
SPC-1 Like IOPS at ms,
STOW still beats WOW by 
%, CSCAN by 
%, and LRW by 
% in a RAID-5
setup. In the RAID-10 setup, where writes become less important (because of no
read-modify-write penalties), STOW still beats WOW by 
% (actually it is much
better at lower response times), CSCAN by 
%, and LRW by 
%.
| |||||||||||||||||||||||||||||||||||
The response time in a lightly loaded system is also an important metric [14]. We present the actual numbers corresponding to RAID-5 in Figure 8 in Table 2.
Note that in all cases, STOW beats the competition easily. However, WOW is unique in that
it requires different thresholds to perform its best for different backend scenarios. While,
choosing a conservative () threshold allows WOW to beat CSCAN and
LRW, WOW is forced to sustain a response time of 
ms in the partial backend
case, even though it could have delivered 
ms response time with a
higher threshold which allows for higher hit ratio.
Since the workload is not known a priori, the right choice of
threshold levels remains elusive for WOW. So, in real life, STOW would
cut the response time not by just 
% (
ms vs ms) when compared to WOW,
but rather by 
% ( ms vs ms).
An adaptive threshold determination scheme might help WOW somewhat,
but in no instance would it be able to compete
with STOW, which at the fixed threshold consistently outperforms its
competition.
![\begin{figure*}\subfigure[Full Backend: Target of $1200$\ IOPS]{
\centerline{
...
...figure=figs/part_P70_C32768_Tvary_rt_RAID5.eps, scale=0.65}
}
}
\end{figure*}](img67.png) |
In Figure 9, we examine how changing the thresholds alone while
keeping the workload constant changes the performance of a write cache.
For WOW and CSCAN, in the full backend case, we can clearly see that as the thresholds become lower,
the performance improves. While the lower thresholds help keep the occupancy
fluctuations away from % occupancy more effectively, it cannot completely
eradicate the phenomenon and, consequently, both WOW and CSCAN fare worse than STOW.
STOW beats WOW and CSCAN by 
% on average, and LRW by 
% in terms of
SPC-1 Like IOPS.
In the partial backend case, both WOW and LRW are better than CSCAN because
they can leverage temporal locality more effectively. Further, the performance
does not depend on the choice of the threshold in this case because what is
gained by keeping lower thresholds is lost in the extra misses incurred in this
high hit ratio scenario.
In terms of SPC-1 Like IOPS, STOW beats WOW by about %, LRW by 
%, and
CSCAN by about %.
![\begin{figure*}\centerline{
\subfigure[Full Backend: Target of 1050 IOPS]{
\ep...
...{figure=figs/part_P80_Cvary_T10_RAID5.eps, scale=0.64}
}
}
\par
\end{figure*}](img71.png) |
Any good adaptive caching algorithm should be able to perform well for all cache
sizes.
In Figure 10(a), we observe that for the full backend scenario,
across all cache sizes, STOW outperforms WOW by 
-%, CSCAN by
-%, and LRW by 
-
%. The gains are
more significant for larger caches because of two reasons: (i) a larger
cache causes the cache occupancy spikes in WOW and CSCAN to be further apart and
much larger in amplitude, making it easier to hit the full-cache condition
(the performance of CSCAN actually dips as the cache size increases
to 
pages!);
(ii) a larger cache in LRW, WOW, and CSCAN proportionally devotes more cache space to
sequential data even though there might be nothing to gain. STOW adapts the
sizes of SeqQ and RanQ, which limits the size of SeqQ in larger caches,
and creates better spatial locality in the larger RanQ.
The partial backend scenario, presented in Figure 10(b),
also indicates that STOW is the best algorithm overall.
With smaller cache sizes, the lower hit ratio overdrives the cache for all
algorithms resulting in very high response times, which are not of much
practical interest.
If we had scaled the workload according to what the cache could support, the benefit
of STOW would be seen consistently even for lower cache sizes. At a cache size
of K pages, in terms of SPC-1 Like IOPS, STOW outperforms WOW by 
%, CSCAN by
%, and LRW by %. The performance at
higher cache sizes is similar for all algorithms because the working set fits in the cache, eliminating the disk bottleneck.
This document was generated using the LaTeX2HTML translator Version 2008 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation stowtop.tex
The translation was initiated by root on 2009-04-21
% full (out of 
K pages). We observe a better average
read response time, but the cache occupancy exhibits spikes
when random data is destaged. When sequential data is destaged, the disks are
under-utilized as shown by the flat steps in the total destages curve.
![\begin{algorithm}
% latex2html id marker 341
[h!]
\caption{STOW: Cache Managemen...
...xtbf{recency-bit} of $g$\ to $0$
\ENDIF
\ENDIF
\end{algorithmic}\end{algorithm}](img27.png)
![\begin{algorithm}
% latex2html id marker 397
[t!]
\caption{STOW: Destage Policy}...
...advanceDestagePtr(currentDestagePtr)}
\ENDWHILE
\end{algorithmic}\end{algorithm}](img31.png)
![\begin{algorithm}
% latex2html id marker 431
[h!]
\caption{STOW: Queue Size Mana...
...RAID5 or RAID10}
\ENDIF
\ENDIF
\ENDIF
\ENDIF
\end{algorithmic}\end{algorithm}](img32.png)
IOPS from
Figure 
IOPS from Figure