![\includegraphics[width=\myfigwidth]{fig/raid.eps}](img9.png)
|

Sung Hoon Baek and Kyu Ho Park
Korea Advanced Institute of Science and Technology
shbaek@core.kaist.ac.kr, kpark@ee.kaist.ac.kr
The frequently-addressed goal of disk prefetching is to make data available in a cache before the data is consumed; in this way, computational operations are overlapped with the transfer of data from the disk. The other goal is to enhance the disk throughput by aggregating multiple contiguous blocks as a single request. Prefetching schemes for a single disk cause problems is used in striped disk arrays. There is a need for a special scheme for multiple disks, in which the characteristics of striped disk arrays [7] are considered.
However, prefetching schemes for disk arrays have been rarely studied. Some offline prefetching schemes (described in Section 1.2.3) take load balancing among disks into account, though they are not practical since they require complete knowledge of future I/O references.
For multiple concurrent reads, the striping scheme of RAID resolves the load balancing among disks [7]. The greater number of concurrent reads implies more evenly distributed reads across striped blocks. As a result, researchers are forced to address five new problems that substantially affect the prefetching performance of striped disk arrays as follows:
In sequential prefetching (described in Section 1.2.4), a large prefetch size laid across multiple disks can prevent parallelism loss. For the worst case of a single stream, the prefetch size must be equal to or larger than the stripe size. However, this method gives rise to prefetching wastage [10] for multiple concurrent sequential reads, which are common in streaming servers. A streaming server that serves tens of thousands of clients, requires several gigabytes of prefetching memory. If the server does not have an over-provisioned memory, thrashing occurs as the prefetched pages are replaced too early by massive prefetches before they are used.
Traditional prefetching schemes have focused on parallelism or the load balance of disks. However, this paper reveals that the independency of disks is more important than parallelism for concurrent reads of large numbers of processes in striped disk arrays, whereas parallelism is only significant when the number of concurrent accesses is roughly less than the number of member disks.
A strip is defined by the RAID Advisory Board [39] as shown in Fig. 1, which illustrates a RAID-5 array consisting of five disks. The stripe is divided by the strips. Each strip is comprised of a set of blocks.
Figure 2(a) shows an example of independency loss. The prefetching requests of conventional prefetching schemes are not aligned in the strip; therefore, a single prefetching request may be split across several disks. In Fig. 2(a), three processes request sequential blocks for their own files. A preset amount of sequential blocks are aggregated as a single prefetching request by the prefetcher. If each prefetch request is not dedicated to a single strip, it is split across two disks, and each disk requires two accesses. For example, if a single prefetch request is for Block 2 to Block 5, the single prefetch request generates two disk commands that correspond to Block 2 & 3 belonging to Disk 0 and Block 4 & 5 belonging to Disk 1. This problem is called independency loss. In contrast, if each prefetching request is dedicated to only one disk, as shown in Fig. 2(b), independency loss is resolved.
To resolve independency loss, each prefetching request must be dedicated to a single strip and not split to multiple disks. The strip size is much less than the stripe size and, as a result, suffers parallelism loss for small numbers of concurrent reads. The two problems, independency loss and parallelism loss, conflict with one other. In the traditional prefetching schemes, if one problem is resolved, the other arises.
We propose an adaptive strip prefetching (ASP) scheme that eliminates almost all demerits of a new strip prefetching scheme, as discussed in Section 2.1. The proposed strip prefetching prefetches all blocks of a strip of a striped disk array on a cache miss. The strip is a set of contiguous blocks dedicated to only one disk, ASP including strip prefetching resolves independency loss. Parallelism loss is resolved by combining ASP with our earlier work, massive stripe prefetching (MSP) [2], which maximizes parallelism for sequential reads of a small number of processes.
![\includegraphics[width=\myfigwidthO]{fig/independency.eps}](img10.png)
|
ASP improves the performance of such workloads because strip prefetching exploits the principle of the spatial locality by implicitly prefetching data that is likely to be referenced in the near future.
We need to divide the traditional meaning of cache hit into prefetch hit and the narrow interpretation of cache hit. The prefetch hit is a read request on a prefetched data that has not yet been referenced by the host since it was prefetched. The cache hit is defined as a read request on a cached data that was loaded by the host's past request.
With the absence of efficient cache management for prefetched data, the low prediction accuracy of strip prefetching exhausts the cache memory. To resolve this problem, ASP early evicts (culls) prefetched data that is less valuable than the least-valuable cached data in an adaptive manner with differential feedback so that the sum of the cache hit rate and the prefetch hit rate of ASP is maximized in a given cache management scheme. The differential feedback has similar features with the adaptive scheme based on marginal utility used in the sequential prefetching in adaptive replacement cache (SARC) [11]. However, there are several differences between SARC and our scheme, which are discussed at the end of Section 2.3.
Several approaches for balancing the amount of memory given to cached data and prefetched data were taken by Patterson et al's transparent informed prefetching [35] and its extension [42]. However, there are many significant differences between them and our scheme. Section 1.2.5 addresses these in more detail.
ASP does not decide which cached data should be evicted and most cache replacement schemes do not take the prefetch hit into account. Hence, ASP may perform well with any of the recent cache replacement policies including RACE [48], ARC [29], SARC [11], AMP [10], and PROMOTE [9].
If a workload exhibits neither prefetch hits nor cache hits, it is apparent that strip prefetching has a greater cost than no prefetching. In this case, any prefetching should be deactivated, even though ASP efficiently culls uselessly prefetched data. For real workloads, ASP exploits an online disk simulation to estimate the two read costs.
History-based prefetching, which records and mines the extensive history of past accesses, is cumbersome and expensive to maintain in practical systems. It also suffers from low predictive accuracy, and the resultant unnecessary reads can degrade performance. Furthermore, it is effective only for stationary workloads.
Speculative execution provides application hints without modifying the code [6]. A copy of the original thread is speculatively executed without affecting the original execution in order to predict future accesses. However, the speculative thread consumes considerable computational resources and can cause misprediction if the future accesses rely on the data of past accesses.
The most common form of prefetching is sequential prefetching (SEQP), which is widely used in a variety of operating systems because sequential accesses are common in practical systems.
The Atropos volume manager [36] dramatically reduces disk positioning time for sequential accesses to two dimensional data structures by means of new data placement in disk arrays. However, Atropos does not give no solution at all to the five problems addressed in Introduction.
Table-based prefetching (TaP) [26] detects these sequential patterns in a storage cache without any help of file systems, and dynamically adjusts the cache size for sequentially prefetched data, namely prefetch cache size, which is adjusted to an efficient size that obtains no more prefetch hit rate above the preset level even if the prefetch cache size is increased. However, TaP fails to consider both prefetch hit rate and cache hit rate.
MSP, which was proposed in our earlier work [2], detects semi-sequential reads at the block level. A sequential read at the file level exhibits a semi-sequential read at the block level because reads at the block level require both metadata access and data access throughout in different regions and the file may be fragmented. If a long semi-sequentiality is detected, the prefetch size of MSP becomes a multiple of the stripe size, and the prefetching request of MSP is aligned in the stripe; as a result, MSP achieves perfect disk parallelism.
Although sequential prefetching is the most popular prefetching scheme in practical systems, sequential prefetching and its variations have until now failed to consider independency loss and they are not at all beneficial to non-sequential reads.
Distinguishing prefetched data from cached data is the common part of TIP, TIPTOE, and our ASP. However, there are notable differences between the first two and ASP. (1) While their eviction policy does not manage uselessly prefetched data, ASP can manage inaccurately prefetched data that are prestaged by strip prefetching. This provides noticeable benefits if the workload exhibits spatial locality. (2) They are based on an approximate I/O service time model to assess the costs for each prefetched block. This deterministic cost estimation may be different from the real costs and cause errors, while ASP uses an adaptive manner that measures and utilizes the instantaneous real cost of prefetched data and cached data. (3) They must scan block caches to find the least-valuable one, while ASP has a negligible overhead with O(1) complexity.
Strip prefetching resolves independency loss by dedicating each prefetching request to a single disk, and resolves parallelism loss when combined with MSP [2]. Adaptive cache culling eliminates the inaccurate prediction of strip prefetching by providing an optimal point that improves both cache hit rate and prefetch hit rate. To guarantee no performance degradation, ASP enables or disables strip prefetching by using a simple online disk simulation. The following sections describe the three new components comprising ASP.
![\includegraphics[width=\fullfigwidth]{fig/acc.eps}](img11.png)
|
To resolve independency loss and to be beneficial for non-sequential reads as well as sequential reads, we propose strip prefetching. Whenever the block requested by the host is not in the cache, strip prefetching reads all blocks of the strip to which the requested block belongs. By grouping consecutive blocks of each strip into a single prefetch unit, strip caches exploit the principle of spatial locality by implicitly prefetching data that is likely to be referenced in the near future. Because each strip is dedicated to only one disk, each prefetch request is not laid across multiple disks; as a result, the problem of independency loss is resolved.
However, strip prefetching has two drawbacks. First, strip prefetching may degrade memory utilization by prefetching useless data. Hence, we propose adaptive cache culling to improve strip prefetching. Adaptive cache culling evicts (culls) prefetched and unused data at the proper time in an adaptive manner; as a result, the sum of the cache hit rate and the prefetch hit rate of ASP is guaranteed to be equal to or larger than those of either strip prefetching or no prefetching.
Second, the read service time of strip prefetching may be longer than that of no prefetching. Hence, ASP activates or deactivates strip prefetching by estimating whether the read cost of is less than not prefetching for the current workload. The estimation can be performed by an online disk simulation with low overhead.
To efficiently manage data prefetched by strip prefetching, as a component of ASP, we propose an adaptive cache culling (ACC) scheme, which maximizes the sum of the cache hit rate and the prefetch hit rate (see Section 1.1.4 for this terminology) of ASP in a given cache management scheme.
Figure 3 illustrates the cache structure that is managed in strip caches, each of which consists of four blocks. ACC manages the cache in strip units. Each strip cache holds the data blocks of a strip. The data block can be a cached block holding cached data, a prefetched block holding prefetched data, or an empty block holding neither memory nor data.
To evict prefetched data earlier than cached data at the proper time
in an adaptive manner (described in Section 2.3), as
shown in Fig. 3, strip caches are partitioned into the
upstream ![]() and the downstream
and the downstream ![]() .
. ![]() can include both prefetched
blocks and cached blocks but
can include both prefetched
blocks and cached blocks but ![]() excludes prefetched blocks. Newly
allocated strip cache that may hold both prefetched blocks and
cached blocks is inserted into
excludes prefetched blocks. Newly
allocated strip cache that may hold both prefetched blocks and
cached blocks is inserted into ![]() . If the number of strip caches in
. If the number of strip caches in
![]() exceeds the maximum number of strip caches that
exceeds the maximum number of strip caches that ![]() can
accommodate, the LRU strip cache of
can
accommodate, the LRU strip cache of ![]() moves to
moves to ![]() , and ACC
culls (evicts) the prefetched blocks of this strip cache.
, and ACC
culls (evicts) the prefetched blocks of this strip cache.
A host request that is delivered to a prefetched block changes it
into a cached block. All cached or prefetched blocks make their way
from upstream toward downstream like a stream of water. If a
prefetched block flows downstream, the prefetched block is changed
into an empty block by culling, which deallocates the memory holding
the prefetched data but retains the information that the block is
empty in ![]() . Thus, blocks requested by the host remain in the cache
for a longer time than prefetched and unrequested blocks. The
average lifetime of prefetched blocks is determined by the size of
. Thus, blocks requested by the host remain in the cache
for a longer time than prefetched and unrequested blocks. The
average lifetime of prefetched blocks is determined by the size of
![]() , which is dynamically adjusted by measuring instant hit rates.
, which is dynamically adjusted by measuring instant hit rates.
ACC changes a variable ![]() , the maximum number of strip caches
that
, the maximum number of strip caches
that ![]() can accommodate, in an adaptive manner. If
can accommodate, in an adaptive manner. If ![]() decreases,
the prefetch hit rate decreases due to a reduced amount of
prefetched data but the cache hit rate increases, otherwise, vice
versa. The system performance depends on the total hit rate that is
the sum of the prefetched hit rate and the cache hit rate. Section
2.3 describes a control scheme for
decreases,
the prefetch hit rate decreases due to a reduced amount of
prefetched data but the cache hit rate increases, otherwise, vice
versa. The system performance depends on the total hit rate that is
the sum of the prefetched hit rate and the cache hit rate. Section
2.3 describes a control scheme for ![]() to maximize
the total hit rate, while this section describes the cache
management and structure of ACC.
to maximize
the total hit rate, while this section describes the cache
management and structure of ACC.
The LRU strip cache of all is evicted under memory pressure. A cache
hit for a strip cache of ![]() and
and ![]() moves the corresponding strip
cache to the MRU position of
moves the corresponding strip
cache to the MRU position of ![]() and
and ![]() , respectively, like the
least recently used (LRU) policy. An evicted strip cache can be a
ghost strip cache, which is designed to improve the performance
using request history. The ghost strip cache has a loose
relationship with the major culling process. Hence, ACC can perform
even if we do not manage the ghost strip cache. The next section
describes the ghost strip cache and some issues.
, respectively, like the
least recently used (LRU) policy. An evicted strip cache can be a
ghost strip cache, which is designed to improve the performance
using request history. The ghost strip cache has a loose
relationship with the major culling process. Hence, ACC can perform
even if we do not manage the ghost strip cache. The next section
describes the ghost strip cache and some issues.
Sibling strip caches are the strip caches corresponding to the strips that belong to the same stripe. Destaging dirty blocks from the RAID cache is more efficient when it is managed in stripes than in blocks or strips [12]. The stripe cache contains sibling strip caches belonging to the stripe. Hence, although a strip cache is evicted, its stripe cache is still alive if at least one sibling strip cache is alive. Therefore, the stripe cache can easily maintain an evicted strip cache as a ghost strip cache.
When all blocks of a strip cache are evicted from the cache, the strip cache becomes a ghost strip cache if one of its sibling strip caches is still alive in the cache. Ghost strip caches hold no memory except for request states of the past. The request states indicate which blocks of the strip cache were requested by the host. When an I/O request is delivered for a ghost strip, the ghost strip becomes alive as a strip cache that retains the past request states. This strip cache that was a ghost is called a reincarnated strip cache, but which has no distinction with the other strip caches except for the past request states.
The past request states of the ghost strip cache works like a kind of history-based prefetching. The past request states remain even after the ghost strip cache is reincarnated. The past cached block, which had not been requested before the block became a ghost, has high possibility of being referenced by the host in the near future although it has not yet been referenced since it was reincarnated. Thus, the culling process does not evict past cached blocks as well as cached blocks.
The cache replacement policy in our implementation is to evict the
LRU strip cache of all. However, ACC does not determine a cache
replacement policy that may evict any cached block in ![]() or
or ![]() . A
new policy for ACC or a combination of a state-of-the-art cache
replacement policy as referenced in Section 1.1.4 and ACC
may provide better performance than the LRU scheme. The exact cache
replacement policy is not within the scope of this paper.
. A
new policy for ACC or a combination of a state-of-the-art cache
replacement policy as referenced in Section 1.1.4 and ACC
may provide better performance than the LRU scheme. The exact cache
replacement policy is not within the scope of this paper.
![\includegraphics[width=\myfigwidthO]{fig/balance.eps}](img12.png)
|
Finding the optimal value of ![]() , the maximum number of strip
caches occupying
, the maximum number of strip
caches occupying ![]() , is the most important part of ACC. We regard
, is the most important part of ACC. We regard
![]() as optimal when it maximizes the total hit rate, which is the
sum of the prefetch hit rate
as optimal when it maximizes the total hit rate, which is the
sum of the prefetch hit rate ![]() and the cache hit rate
and the cache hit rate ![]() . Fig.
4 illustrates a function of the total hit rate with
respect to
. Fig.
4 illustrates a function of the total hit rate with
respect to ![]() . When the slope of the function is zero, the total
hit rate is at the maximum.
. When the slope of the function is zero, the total
hit rate is at the maximum.
As ![]() increases,
increases, ![]() increases but the incremental rate of
increases but the incremental rate of ![]() declines. As
declines. As ![]() decreases,
decreases, ![]() increases and the incremental rate
of
increases and the incremental rate
of ![]() declines. Therefore, the derivative of
declines. Therefore, the derivative of ![]() with respect to
with respect to
![]() ,
, ![]() , is a monotonically decreasing function
and so is the negative derivative of
, is a monotonically decreasing function
and so is the negative derivative of ![]() with respect to
with respect to ![]() ,
,
![]() . Then, there is zero or one cross point of these
derivatives. The function of
. Then, there is zero or one cross point of these
derivatives. The function of ![]() with respect to
with respect to ![]() can form a
hill shape or be an monotonically increasing or deceasing function,
these three types of functions have only one peak point.
can form a
hill shape or be an monotonically increasing or deceasing function,
these three types of functions have only one peak point.
If we can determine the instant value of the slope for the current
![]() , the optimal
, the optimal ![]() can be achieved using the following
feedback with the instant value of the slope.
can be achieved using the following
feedback with the instant value of the slope.
When ![]() is on the left side of Fig 4, the
feedback increases
is on the left side of Fig 4, the
feedback increases ![]() by the positive value of the slope. If
by the positive value of the slope. If
![]() increases so much that the slope becomes negative, the
feedback with the negative slope decreases
increases so much that the slope becomes negative, the
feedback with the negative slope decreases ![]() so that the total
hit rate is near the peak. Even if
so that the total
hit rate is near the peak. Even if ![]() is an increasing or
decreasing function, the above feedback finds the optimal value of
is an increasing or
decreasing function, the above feedback finds the optimal value of
![]() .
.
The function of the slope is the derivative of the total hit rate
![]() , which is the sum of the two derivatives of
, which is the sum of the two derivatives of ![]() and
and ![]() with
respect to
with
respect to ![]() as the following equation.
as the following equation.
slope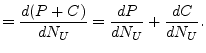 |
(2) |
![\includegraphics[width=\myfigwidthO]{fig/differential.eps}](img17.png)
|
An approximated derivative can be measured as shown in Fig.
5. By the definition of differential, the
derivative of ![]() is similarly equal to the number of prefetch hits
is similarly equal to the number of prefetch hits
![]() that, during a time interval, occur in the
that, during a time interval, occur in the
![]() strip caches additionally allocated to
strip caches additionally allocated to ![]() . The additional
prefetch hit rate
. The additional
prefetch hit rate
![]() is similar to
is similar to
![]() , which
is the prefetch hit rate of the strip caches of the upstream bottom
that is adjacent to the additionally allocated strip caches.
Therefore, the derivative of the prefetch hit rate with respect to
, which
is the prefetch hit rate of the strip caches of the upstream bottom
that is adjacent to the additionally allocated strip caches.
Therefore, the derivative of the prefetch hit rate with respect to
![]() can be approximated with the following equation.
can be approximated with the following equation.
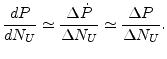 |
(3) |
If the upstream ![]() increases by
increases by
![]() , the downstream
, the downstream ![]() decreases by
decreases by
![]() . The coefficient
. The coefficient ![]() is
determined by the occupancy ratio of the non-empty blocks in both
the expanded portion of
is
determined by the occupancy ratio of the non-empty blocks in both
the expanded portion of ![]() and the shrunk portion of
and the shrunk portion of ![]() (see Eq.
(6)). The derivative of the cache hit rate with respect
to
(see Eq.
(6)). The derivative of the cache hit rate with respect
to ![]() is similar to the cache hit rate
is similar to the cache hit rate
![]() that
occurs in the
that
occurs in the
![]() strip caches of the global bottom.
If we want to monitor the cache hit rate,
strip caches of the global bottom.
If we want to monitor the cache hit rate, ![]() , in a fixed
size of the global bottom, the derivative of the cache hit rate can
be approximated with the following equation.
, in a fixed
size of the global bottom, the derivative of the cache hit rate can
be approximated with the following equation.
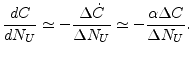 |
(4) |
The differential value (slope) of the current partition can be
obtained by monitoring the number of prefetch hits ![]() occurring in the upstream bottom and the number of cache hits
occurring in the upstream bottom and the number of cache hits
![]() occurring in the global bottom during a time interval.
occurring in the global bottom during a time interval.
The upstream bottom ![]() is the bottom portion of
is the bottom portion of ![]() , where the
number of strip caches of
, where the
number of strip caches of ![]() is predetermined as 20% of the
maximum number of strip caches of the simple strip prefetching
policy. Similarly, the global bottom
is predetermined as 20% of the
maximum number of strip caches of the simple strip prefetching
policy. Similarly, the global bottom ![]() is the bottom portion of
the global list (the combination of
is the bottom portion of
the global list (the combination of ![]() and
and ![]() ). At an initial
stage or in some other cases,
). At an initial
stage or in some other cases, ![]() contains no strip cache or too
small number of strip caches. Hence,
contains no strip cache or too
small number of strip caches. Hence, ![]() can overlap with
can overlap with ![]() .
.
![]() accommodates the same number of strip caches as
accommodates the same number of strip caches as ![]() .
.
By combining Eqs. (1) and (5), the final feedback operation that achieves the maximum hit rate can be written as in the following process.
The upstream size ![]() is initially set to the cache size over the
strip size. Until the cache is fully filled with data, ASP activates
strip prefetching and
is initially set to the cache size over the
strip size. Until the cache is fully filled with data, ASP activates
strip prefetching and ![]() is not changed by the feedback. At the
initial time,
is not changed by the feedback. At the
initial time, ![]() does not exist, and thus,
does not exist, and thus, ![]() is identical to
is identical to
![]() .
.
We do not let ![]() fall below the size of
fall below the size of ![]() to retain the fixed
size of
to retain the fixed
size of ![]() . If
. If ![]() shrinks to the size of
shrinks to the size of ![]() , ACC
deactivates strip prefetching until
, ACC
deactivates strip prefetching until ![]() swells to twice the size
of
swells to twice the size
of ![]() to make a hysteresis curve. The reason of this deactivation
is that too small
to make a hysteresis curve. The reason of this deactivation
is that too small ![]() indicates strip prefetching is not
beneficial in terms of not only hit rate but also read service time.
indicates strip prefetching is not
beneficial in terms of not only hit rate but also read service time.
The differential feedback has similar features with the adaptive
manner based on marginal utility used in the sequential prefetching
in adaptive replacement cache (SARC) [11]. However, we
present a formal method that finds an optimal point using the
derivatives of cache hit rate and prefetch hit rate. Only our
analytical approach can explain the feedback coefficient ![]() .
Furthermore, there are several differences between the two
algorithms: (1) while SARC does not distinguish prefetched blocks
from cached blocks, our scheme takes care of the eviction of only
prefetched blocks that are ignored in SARC, (2) SARC relates to
random data and sequential data, whereas the proposed scheme
considers both prefetch hits and cache hits in a prefetching
scenarios, and (3) our scheme manages the caches in terms of strips
for an efficient management of striped disk arrays, while SARC has
no feature for disk arrays.
.
Furthermore, there are several differences between the two
algorithms: (1) while SARC does not distinguish prefetched blocks
from cached blocks, our scheme takes care of the eviction of only
prefetched blocks that are ignored in SARC, (2) SARC relates to
random data and sequential data, whereas the proposed scheme
considers both prefetch hits and cache hits in a prefetching
scenarios, and (3) our scheme manages the caches in terms of strips
for an efficient management of striped disk arrays, while SARC has
no feature for disk arrays.
For example, if ![]() decreases to the minimum value due to the lack
of prefetch hits, ASP must deactivate strip prefetching. The
deactivation, however, cannot rely on the minimum size of
decreases to the minimum value due to the lack
of prefetch hits, ASP must deactivate strip prefetching. The
deactivation, however, cannot rely on the minimum size of ![]() because
because ![]() may not shrink if both the prefetch hit rate and cache
hit rate are zero or extremely low. Therefore, ASP employs an online
disk simulation, which investigates whether strip prefetching
requires a greater read cost than no prefetching.
may not shrink if both the prefetch hit rate and cache
hit rate are zero or extremely low. Therefore, ASP employs an online
disk simulation, which investigates whether strip prefetching
requires a greater read cost than no prefetching.
Whenever the host requests a block, ASP calculates two read costs,
![]() and
and
![]() , by using an online disk
simulation with a very low overhead. The disk cost
, by using an online disk
simulation with a very low overhead. The disk cost
![]() is the virtual read time spent in disks for all the blocks of the
cache by pretending that strip prefetching has always been
performed. Similarly, the disk cost
is the virtual read time spent in disks for all the blocks of the
cache by pretending that strip prefetching has always been
performed. Similarly, the disk cost
![]() is the virtual
read time spent in disks for all blocks of the current cache by
pretending that no prefetching has ever been performed.
is the virtual
read time spent in disks for all blocks of the current cache by
pretending that no prefetching has ever been performed.
Whenever the host requests a block that is not in the cache, ASP
compares
![]() with
with
![]() . If
. If
![]() is less than
is less than
![]() , ASP deactivates strip prefetching
for this request because strip prefetching is estimated to have
provided slower read service time than no prefetching for all recent
I/Os that have affected the current cache.
, ASP deactivates strip prefetching
for this request because strip prefetching is estimated to have
provided slower read service time than no prefetching for all recent
I/Os that have affected the current cache.
If a block hits the cache as a result of strip prefetching, the block must be one of all the blocks in the cache. The gain of strip prefetching is therefore correlated with all blocks in the cache that contains the past data. Hence, all blocks in the cache are exploited to determine whether strip prefetching provides a performance gain.
The cache is managed in terms of strips and consists of ![]() strip
caches, and each strip cache,
strip
caches, and each strip cache, ![]() , has two variables,
, has two variables,
![]() and
and
![]() , which are updated by
the online disk simulation for every request from the host to the
strip cache
, which are updated by
the online disk simulation for every request from the host to the
strip cache ![]() . The variable
. The variable
![]() is the virtual
read time spent in
is the virtual
read time spent in ![]() if we assume that no prefetching has ever
been performed. The variable
if we assume that no prefetching has ever
been performed. The variable
![]() is the virtual
read time spent in
is the virtual
read time spent in ![]() if we assume that strip prefetching has
always been performed. Then we can express
if we assume that strip prefetching has
always been performed. Then we can express
![]() and
and
![]() as follows:
as follows:
From Eq.(8),
![]() can be obtained by the
sum of
can be obtained by the
sum of
![]() for all strip caches. It seems to
require a great overhead. However, an equivalent operation with O(1)
complexity can be achieved as follows: (1) Whenever the host causes
a cache miss on a new block whose strip cache is not in
for all strip caches. It seems to
require a great overhead. However, an equivalent operation with O(1)
complexity can be achieved as follows: (1) Whenever the host causes
a cache miss on a new block whose strip cache is not in ![]() ,
calculate the disk cost to read all blocks of the requested strip
and add it to both
,
calculate the disk cost to read all blocks of the requested strip
and add it to both
![]() and
and
![]() ; (2)
whenever a read request accesses to a prefetched block or misses the
cache, calculate the virtual disk cost to access to the block even
though the request hits the cache, and add the disk cost to both
; (2)
whenever a read request accesses to a prefetched block or misses the
cache, calculate the virtual disk cost to access to the block even
though the request hits the cache, and add the disk cost to both
![]() and
and
![]() of the strip cache
of the strip cache ![]() to which the requested block belongs; and (3) subtract
to which the requested block belongs; and (3) subtract
![]() from
from
![]() and subtract
and subtract
![]() from
from
![]() when the strip cache
when the strip cache
![]() is evicted from the cache.
is evicted from the cache.
ASP suffers parallelism loss when there are only a small number of sequential reads. In other words, disks are serialized for a single stream because each request of ASP is dedicated to only one disk. However, the combination of ASP and massive stripe prefetching (MSP), which was briefly described in Section 1.2.4, resolves the parallelism loss of ASP without interfering with the ASP operation and without losing the benefit of ASP.
To combine ASP with MSP, we need the following rules:
The reading by MSP does not change any of the cost variables of ASP.
When ASP tries to reference a block prefetched by MSP, ASP updates
![]() and
and
![]() as if the block has not been
prefetched. MSP excludes blocks which are already in the cache or
being read or prefetched by ASP or MSP from blocks that are assigned
to be prefetched by MSP. ASP culls strip caches prefetched by MSP as
well as strip prefetching.
as if the block has not been
prefetched. MSP excludes blocks which are already in the cache or
being read or prefetched by ASP or MSP from blocks that are assigned
to be prefetched by MSP. ASP culls strip caches prefetched by MSP as
well as strip prefetching.
The system in the experiments uses dual 3.0 GHz 64-bits Xeon
processors, 1 GiB of main memory, two Adaptec Ultra320 SCSI host bus
adapters, and five ST373454LC disks, each of which has a speed of
15,000 revolutions per minute (rpm) and a 75 Gbyte capacity - GiB is
the abbreviation of gibibyte, as defined by the International
Electrotechnical Commission. 1 GiB refers to ![]() bytes, whereas
1 GB refers to
bytes, whereas
1 GB refers to ![]() bytes. [17]. The five disks
comprise a RAID-5 array with a strip size of 128 KiB. A Linux kernel
(version 2.6.18) for the x86_64 architecture runs on this machine;
the kernel also hosts the existing benchmark programs, the ext3 file
system, the anticipatory disk scheduler, and our RAID driver,
namely, the Layer of RAID Engine (LORE) driver. Apart from the page
cache of Linux, the LORE driver has its own cache memory of 500 MiB
just as hardware RAIDs have their own cache. The block size is set
to 4 KiB.
bytes. [17]. The five disks
comprise a RAID-5 array with a strip size of 128 KiB. A Linux kernel
(version 2.6.18) for the x86_64 architecture runs on this machine;
the kernel also hosts the existing benchmark programs, the ext3 file
system, the anticipatory disk scheduler, and our RAID driver,
namely, the Layer of RAID Engine (LORE) driver. Apart from the page
cache of Linux, the LORE driver has its own cache memory of 500 MiB
just as hardware RAIDs have their own cache. The block size is set
to 4 KiB.
In our experiments, we compare all possible combinations of our scheme (ASP) and the existing schemes (MSP and SEQP): namely ASP, MSP, SEQP, ASP+MSP, ASP+SEQP, MSP+SEQP, and ASP+MSP+SEQP. The method of combining ASP and MSP is described in Section 2.5. ASP and MSP operate in the LORE driver while SEQP is performed by the virtual file system (VFS) that is independent of the LORE driver. By simply turning on or off the SEQP of VFS, we can easily combine SEQP with ASP or MSP without any rules.
In all the figures of this paper, SEQPX denotes a SEQP with X kibibytes of the maximum prefetch size. For example, SEQP128 indicates that the maximum prefetch size is 128 KiB. All the experimental results are obtained from six repetitions. For some of the results that exhibit significant deviation, each standard deviation is displayed in its graph.
Figure 6 is the results of the general hard disk drive usage of PCMark that contains disk activities from using several common applications. In this experiment, we compare ASP, strip prefetching (SP), and no prefetching. SP exhibits the highest prefetch hit rate while no prefetching provides the highest cache hit rate. ASP outperforms both SP and no prefetching at all of the cases in Fig. 6. With an over-provisioned memory, the throughput of SP is similar with that of ASP. However, ASP is significantly superior to SP with 400 MiB or less of the RAID cache. At the bast case, ASP outperforms SP by 2 times and no prefetching by 2.2 times with 400 MiB of the RAID cache.
![\includegraphics[width=1.05\mygraphwidthO]{fig/dbench500.eps}](img47.png)
|
The benchmark Dbench (version 3.04) [43] produces a local file system load. It does all the same read and write calls that the smbd server in Samba [37] would produce when confronted with a Netbench [30] run. Dbench generates realistic workloads consisting of so many cache hits, prefetch hits, cache misses, and writes that the ability of ASP can be sufficiently evaluated.
Figure 7 shows the results of Dbench. We divided the main memory of 1 GiB into 512 MiB for the Linux system, 500 MiB for the RAID cache, 12 MiB for the RAID driver. It took 10 minutes for each run.
![\includegraphics[width=\mygraphwidth]{fig/tiothru1.eps}](img48.png)
(a) Throughput
|
Both ASP and ASP+MSP rank the highest in Fig. 7
and outperform strip prefetching (SP) by 20% for 128 clients. In
this experiment, ![]() was always less than
was always less than ![]() ; hence, the
gain of ASP over SP originated from ACC. ASP outperforms SEQP32 by 2
times for 128 clients and a hardware-based RAID by 11 times for 64
clients and by 7.6 times for 128 clients. The hardware-based RAID,
which is an Intel SRCU42X with a 512 MiB memory, has write-back with
a battery pack, cached-IO, and adaptive read-ahead capabilities.
; hence, the
gain of ASP over SP originated from ACC. ASP outperforms SEQP32 by 2
times for 128 clients and a hardware-based RAID by 11 times for 64
clients and by 7.6 times for 128 clients. The hardware-based RAID,
which is an Intel SRCU42X with a 512 MiB memory, has write-back with
a battery pack, cached-IO, and adaptive read-ahead capabilities.
For a fair comparison, the memory of the Linux system for the hardware-based RAID was given the same size (512 MiB) as in the case of our RAID driver, and to compensate the memory occupied by the firmware of the hardware RAID, the cache of our RAID driver is tuned to 500 MiB that is slightly smaller than the internal memory of the hardware RAID. The sequential prefetching of Linux is turned on for the hardware RAID.
Sequential prefetching (SEQP) itself and combinations with SEQP significantly degrade throughput by causing independency loss. Furthermore, because redundant prefetched data that exist in both the RAID cache with ASP and the page cache of Linux with SEQP inefficiently consume cache memory. The addition of SEQP to ASP is inferior to ASP due to independency loss and redundant prefetched data. In addition, the adaptive culling operates inefficiently because prefetched data that are requested by SEQP of the host are considered cached data from the viewpoint of the RAID cache with ASP. Although ASP+SEQP128 is inferior to ASP, it outperforms SEQP128 by 67% for 128 clients.
SEQP with a large prefetch size suffers from cache wastage for a large number of processes. As shown in Fig. 7, SEQP32 outperforms SEQP512 by 4% for 64 clients and by 15% for 128 clients. In contrast, Fig. 9(a) shows that an increase in the maximum prefetch size of SEQP improves disk parallelism for a small number of processes.
``ASP w/o ghost" in Fig. 7 indicates the improved culling effect with the past cached block. ASP outperforms ASP without the ghost by 14% for 128 clients. The addition of MSP to ASP slightly degrades ASP. However, the addition of MSP can resolve parallelism loss for small numbers of processes or a single process. Section 3.5 shows the evaluation of parallelism loss.
We used the benchmark Tiobench (version 0.3.3) [24] to evaluate whether the disk simulation of ASP makes the right decision on the basis of the workload property. Figure 8(a) shows the throughput of random reads with four threads, 40,000 read transactions, and 4 KiB of the block size in relation to a varied aggregate file size (workspace size). A random read with a small workspace size of 0.6 GiB exhibits such high spatial locality that ASP outperforms SEQP128. With a workspace size of 0.8 GiB, ASP outperforms both SP and SEQP. When the workspace size is equal to or larger than 1 GiB, ASP outperforms SP and show the same throughput as SEQP by deactivating SP. For random reads, SEQP does not prefetch anything. This random read with the large workspace generates so few cache hits that the adaptive cache culling does not improve the throughput of ASP.
![\includegraphics[width=\mygraphwidth]{fig/conseq.eps}](img54.png)
(a) Forward read
|
Figure 8(b) shows that when combined with other prefetching schemes MSP is effectively disabled without interfering with the combined prefetching scheme for random reads.
Figure 8(c) shows the CPU load over throughput and the standard deviation for the random reads. Although ASP+SEQP128 requires a greater computational overhead than SEQP128, Fig. 8(c) shows that the CPU load over throughput of ASP+SEQP128 is less than or almost equal to that of SEQP128. Thus, the computational overhead of ASP is too low to be measured.
In spite of its throughput gain, SP may cause the latency to increase because it reads more blocks than no prefetching. However, the performance enhancement by the gain of SP decreases the latency. Figure 8(d) shows that the maximum latency of SEQP128 is longer than that of SP and ASP when SP is beneficial.
This section evaluates the decision correctness and overhead of ASP for the two types of workloads, which may or may not be beneficial to SP. However, because many types of reads exhibit spatial locality, many realistic workloads are beneficial to SP. The next sections show the performance evaluation for various workloads that exhibit spatial locality.
We used the benchmark IOzone (version 3.283) [32] for the three types of concurrent sequential reads: the forward read, the reverse read, and the stride read. We vary the number of processes from one to 16 with a fixed aggregate file size of 2 GiB and a block size of 4 KiB.
As shown in Fig. 9(a), MSP boosts and dominates the forward sequential throughput when the number of processes is two or four as well as one. The combination of ASP and MSP (ASP+MSP) shows 5.8 times better throughput than ASP for a single stream because ASP suffers the parallelism loss. When the number of processes is four, ASP+MSP also outperforms ASP by 76%.
When the number of process is one, ASP+MSP outperforms SEQP512 by 134% and SEQP32 by 379%. SEQP, If sequential prefetching has the larger prefetch size, it may resolve the parallelism loss for a small number of streams. However, this approach causes cache wastage and independency loss for concurrent multiple sequential reads. When the number of streams is 16, ASP+MSP outperforms ASP+MSP+SEQP128 by 33% because a combination with SEQP gives rise to independency loss.
For the reverse sequential reads shown in Fig. 9(b), MSP and SEQP do not prefetch any block and, as a consequence, severely degrade the system throughput. ASP is the best for the reserve reads and outperforms SEQP by 41 times for 16 processes.
Figure 9(c) and 9(d) show the throughput results of the stride reads; these results were obtained with IOzone. A stride read means a sequentially discontiguous read with a fixed stride distance that is defined by the number of blocks between discontiguous reads. Stride reads cause additional revolutions in some disk models, thereby degrading the throughput. This problem was unveiled in [3]. The stride reads shown in Fig. 9 are significantly beneficial to MSP and ASP because they prefetch contiguous blocks regardless of stride requests.
Figures 9(c) and 9(d) show that as the stride distance decreases, the throughput of the combinations with ASP increases, whereas the throughput of SEQP decreases. ASP+MSP outperforms any of SEQPs by 84.6 times for a single process when the stride distance is three blocks. As the number of processes increases, MSP is deactivated and ASP dominates the throughput of the stride reads. In Fig. 9(d), the combinations with ASP outperform the combinations without ASP by at least 9.44 times when the number of processes is 16.
The TPC BenchmarkTMH (TPC-H) is a decision support benchmark that runs a suite of business-oriented ad-hoc queries and concurrent data modifications on a database system. Figure 10 shows the results of the queries of TPC-H running on a MySQL database system with the scale factor of one.
Most read patterns of TPC-H are stride reads and non-sequential reads with spatial locality [48], which are highly beneficial to ASP but not to SEQP. ASP and ASP+MSP outperform SEQP128 by 1.7 times and 2.2 times, respectively, on average for the 12 queries. ASP+MSP and ASP+MSP+SEQP are the best for all the 12 queries of TCP-H. Query four (Q4) delivers the best performance of ASP+MSP with 8.1 times better throughput than that of SEQP128.
The MySQL system with TPC-H exhibits neither independency loss nor enough cache hits at the global bottom. Hence, most of ASP's superior performance originates from the principle of the spatial locality of SP. In the experiments in the next section, we do not compare ASP with SP for the same reason.
This section presents the results of cscope [38], glimpse [28], link, and booting as real applications.
The developer's tool cscope, which is used for browsing source code, can build the symbol cross-reference of C source files and allow users to browse through the C source files. Figure 11 shows the turnaround time that is required for cscope to index the symbol cross-reference of the Linux kernel (2.6.18) source files. In Fig. 11, cscope1 means that the symbol indexing is performed without object files that are the results of compilation. The symbol indexing of cscope2 is performed with source files and object files.
Because cscope is an application that uses a single thread, SEQP does not cause independency loss. Hence, ASP+MSP+SEQP128 shows the best performance and ASP+MSP shows the next best performance. However, ASP+MSP+SEQP128 slightly outperforms ASP+MSP by 0.65% for cscope1 and 1.2% for cscope2. In addition, ASP+MSP outperforms SEQP by 2.1 times in cscope1 and by 38 % in cscope2.
In the cscope2 experiment with both the source files and the object files, the performance gap between ASP+MSP and SEQP decreases. In other words, ASP prefetches unnecessary data because the required source files and the unnecessary object files are interleaved. However, ASP+MSP outperforms SEQP by at least 41%.
![\includegraphics[width=\mygraphwidth]{fig/cscope.eps}](img59.png)
|
Figure 12 shows the execution time needed for glimpse, a text information retrieval application from the University of Arizona, to index the text files in ``/usr/share/doc" of Fedora Core 5 Release. The results of glimpse resemble the results of cscope1. ASP+MSP and ASP+MSP+SEQP128 outperform SEQP128 by 106%.
The link of Fig. 12 shows the turnaround time for gcc to link the object files of the Linux kernel. The results are obtained by executing ``make vmlinux" in the kernel source directory after executing ``make vmlinux" and ``rm vmlinux". The link operation requires a high computational overhead and small reads that inspect the modification date of the source files. However, ASP+MSP outperforms SEQPs by at least 10%.
![\includegraphics[width=\mygraphwidth]{fig/glimpselink.eps}](img60.png)
|
Figure 13 shows the Linux booting speed. The Linux booting consists of partially random reads for scattered applications and script files. We partitioned the booting sequence into two phases. Phase 1 shown in Fig. 13 is the time that elapses from just before the running of the ``init" process to just before the remounting of the root file system in read-write mode. Phase 2 is the time that elapses from the end of Phase 1 to just after the completion of all the booting scripts (/etc/rc3.d/S* files).
Phase 1 consists of CPU-bounded operations rather than I/O-bounded operations. Hence, the gain of ASP is small. Phase 2, on the other hand, requires I/O bounded operations. Because Linux booting does not produce multiple concurrent reads and consequently causes no independency loss, the best scheme for the Linux booting is ASP+MSP+SEQP128 rather than ASP+MSP. However, the performance gap is negligible. In Phase 2, ASP+MSP outperforms SEQP128 by 46% and SEQP512 by 34%.
![\includegraphics[width=\mygraphwidth]{fig/booting.eps}](img61.png)
|
From the results of Dbench and IOzone, we see that SEQP suffers both parallelism loss and independent loss, but ASP and ASP+MSP are free from them. Additionally, the results of Dbench show that ASP efficiently manages prefetched data. As a result, the sum of the prefetch hit rate and cache hit rate is equal to or greater than that of strip prefetching and no prefetching. The experiments using Tiobench show that ASP has a low overhead and wisely deactivates SP if SP is not beneficial to the current workload. In the results of Dbench, ASP outperforms SEQP128 by 2.3 times and a hardware RAID controller (SRCU42X) by 11 times. The experimental result with PCMark shows that ASP is 2 times faster than SP due to the culling scheme. From the experiments using TPC-H, cscope, link, glimpse, and Linux booting, we can perceive that many realistic workloads exhibit high spatial locality. ASP+MSP is 8.1 times faster than SEQP128 for the query four of TPC-H, and outperforms SEQP by 2.2 times on average for the 12 queries of TPC-H.
Among all the prefetching schemes and combinations presented in this
paper, ASP and ASP+MSP rank the highest. We implemented a RAID
driver with our schemes in a Linux kernel. Our schemes have a low
overhead, and can be used in various RAID systems ranging from
entry-level to enterprise-class.
The source code of our RAID driver is downloadable from https://core.kaist.ac.kr/dn/lore.dist.tgz, but you may violate some patent rights belonging to KAIST if you commercially use the code.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation baek
The translation was initiated by root on 2008-04-29