Next: Predictability over time Up: Predicting node resources Previous: Predicting node resources

We first investigate the correlation among attributes on the same node. A high correlation would allow us to use the value of one attribute on the node to predict the values of other attributes on the node. Table 2 shows the correlation coefficient (r) among attributes on the same node, based on data from all nodes and all timesteps in our trace. Somewhat surprisingly, we see no strong correlations--we might expect to see a correlation between load and network bandwidth, free memory, or swap space. Instead, because each PlanetLab node is heavily multiprogrammed, as suggested by Figure 1, the overall resource utilization is an average (aggregate) across many applications. A spike in resource consumption by one application might occur at the same time as a dip on resource consumption by another application, leaving the net change ``in the noise.'' We found a similar negative result when examining the correlation of a single attribute across nodes at the same site (e.g., between load on pairs of nodes at the same site). While we initially hypothesized that there may be some correlation in the level of available resources within a site, for instance because of user preference for some geographic or network locality, the weakness of these same-site correlations implies that we cannot use measurements of a resource on one node at a site to predict values of that resource on other nodes at the site.
|
One pair of potentially correlated attributes that merits special attention is inter-node latency and bandwidth. In general, for a given loss rate, one expects bandwidth to vary roughly with 1/latency [16]. If we empirically find a strong correlation between latency and bandwidth, we might use latency as a surrogate for bandwidth, saving substantial measurement overhead.
To investigate the potential correlation, we annotated each pairwise available bandwidth measurement collected by Iperf with the most recently measured latency between that pair of nodes. We graph these (latency,bandwidth) tuples in Figure 19. Fitting a power law regression line, we find a correlation coefficient of -0.59, suggesting a moderate inverse power correlation. One reason why the correlation is not stronger is the presence of nodes with limited bandwidth (relative to the bulk of other nodes), such as DSL nodes and nodes configured to limit outgoing bandwidth to 1.5 Mb/s or lower. These capacity limits artificially lower available bandwidth below what would be predicted based on the latency-bandwidth relationship from the dataset as a whole. Measurements taken by nodes in this category correspond to the dense rectangular region at the bottom of Figure 19 below a horizontal line at 1.5 Mb/s, where decreased latency does not correlate to increased bandwidth.
When such nodes are removed from the regression equation computation, the correlation coefficient improves to a strong -0.74. Viewed another way, using a regression equation derived from all nodes to predict available bandwidth using measured latency leads to an average 233% error across all nodes. But if known bandwidth-limited nodes are excluded when computing the regression equation, predicting available bandwidth using measured latency leads to only an average 36% error across the non-bandwidth-limited nodes. Additionally, certain node pairs show even stronger latency-bandwidth correlation. For example, 48% of node pairs have bandwidths within 25% of the value predicted from their latency. We conclude that a power-law regression equation computed from those nodes with ``unlimited'' bandwidth (not DSL or administratively limited) allows us to accurately predict available bandwidth using measured latency for the majority of those non-bandwidth-limited nodes. This in turn allows a resource discovery system to reduce measurement overhead by measuring bandwidth among those nodes infrequently (only to periodically recompute the regression equation), and to use measured latency to estimate bandwidth the rest of the time. Of course, if the number of bandwidth-capped nodes in PlanetLab increases, then more nodes would have to be excluded and this correlation would become of less value.
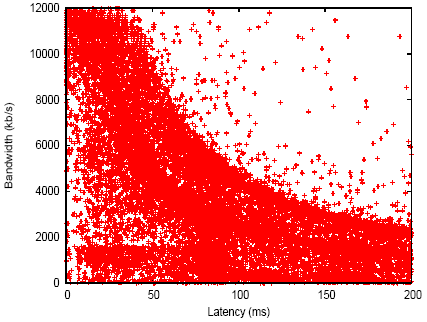
Figure 19: Correlation between latency and available bandwidth. Each point represents one end-to-end bandwidth measurement and the latency measurement between the same pair of nodes taken at the closest time to that of the bandwidth measurement.
David Oppenheimer 2006-04-14