


Next: Failure of high connectivity
Up: Geographic fault tolerance of
Previous: Geographic fault tolerance of
The degree of a node provides a first-level quantification of the
fault tolerance of that node in a given topology. A node with a degree
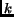 can tolerate up to
can tolerate up to 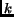 geographic failures before getting
completely disconnected from all other nodes in the topology. In
particular, a leaf node is not resilient to the geographic failure of
its neighbor, but the failure of a leaf node itself has minimal impact
on the rest of the network. On the other hand, the failure of a node
with a very high degree would impact its many neighbors (corresponding
to many different geographic regions).
Given complete freedom in placing
geographic failures before getting
completely disconnected from all other nodes in the topology. In
particular, a leaf node is not resilient to the geographic failure of
its neighbor, but the failure of a leaf node itself has minimal impact
on the rest of the network. On the other hand, the failure of a node
with a very high degree would impact its many neighbors (corresponding
to many different geographic regions).
Given complete freedom in placing 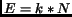 edges on
edges on 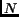 nodes, it is
possible to construct a topology that has a minimum vertex-cut of
nodes, it is
possible to construct a topology that has a minimum vertex-cut of
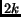 . In other words, the
. In other words, the 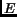 edges can be placed in such a way that
even in the presence of any
edges can be placed in such a way that
even in the presence of any 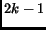 node failures in the graph, the
resulting topology will still remain connected. We term such a
placement of edges that maximizes the size of the vertex cut as an
optimal placement. In the optimal placement, all the vertices
have the same degree, viz.
node failures in the graph, the
resulting topology will still remain connected. We term such a
placement of edges that maximizes the size of the vertex cut as an
optimal placement. In the optimal placement, all the vertices
have the same degree, viz. 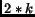 . For the simple case of
. For the simple case of 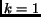 , the
optimal placement results in a ring topology. Although this optimal
placement may be difficult to construct due to practical constraints,
it provides us a nice reference point for comparing the fault
tolerance of ISP topologies. In order to contrast an ISP's topology
from the optimal scenario, we look at the degree distribution of the
nodes. We say that a graph has a skewed degree distribution if
its node degrees are distributed over a wide range with a few large
node degrees and a high percentage of the nodes are leaves. The
Internet topology exhibits a skewed degree distribution which can
be characterized by a power law as described in [4].
, the
optimal placement results in a ring topology. Although this optimal
placement may be difficult to construct due to practical constraints,
it provides us a nice reference point for comparing the fault
tolerance of ISP topologies. In order to contrast an ISP's topology
from the optimal scenario, we look at the degree distribution of the
nodes. We say that a graph has a skewed degree distribution if
its node degrees are distributed over a wide range with a few large
node degrees and a high percentage of the nodes are leaves. The
Internet topology exhibits a skewed degree distribution which can
be characterized by a power law as described in [4].
Figure 15:
Degree Distribution of Geographic Topologies of ISPs
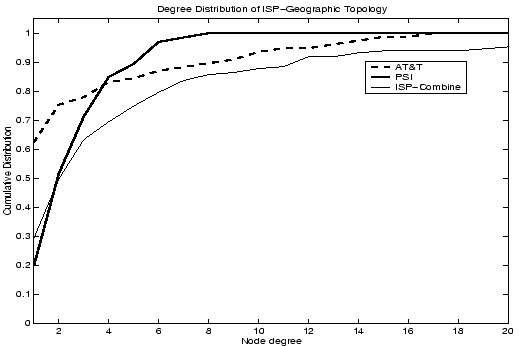 |
Among the 9 commercial ISPs, some of them such as AT&T and Genuity
have a very skewed degree distributions while other ISPs such as
PSINet and Verio have much less skewed degree distributions (closer to
optimal). The degree distribution will not be affected much due to a
few missing links. Figure 15 shows the degree
distributions of AT&T and PSINet. AT&T's topology has the maximum
percentage of leaves among the 9 ISP topologies (62%) and has a few
nodes with a degree greater than 12 (Chicago, Dallas). On the other
hand, more than 50% of PSINet's nodes have a degree of either 2 or 3.
This matches the optimal degree for Verio given that it has an edge to
node ratio 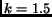 , which corresponds to an optimal degree of
, which corresponds to an optimal degree of 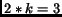 . The ISP-Combine curve shows the degree distribution of the
geographic topology obtained by combining the topology graphs of all 9
ISPs. The geographic nodes corresponding to the same city in the
individual ISP topologies map to a single node in the combined
topology. The combined topology still has a significant skew in its
degree distribution.
. The ISP-Combine curve shows the degree distribution of the
geographic topology obtained by combining the topology graphs of all 9
ISPs. The geographic nodes corresponding to the same city in the
individual ISP topologies map to a single node in the combined
topology. The combined topology still has a significant skew in its
degree distribution. 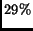 of the nodes continue to be leaves. This
happens despite the combined topology having an edge to node ratio of
of the nodes continue to be leaves. This
happens despite the combined topology having an edge to node ratio of
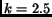 , which corresponds to an optimal degree of 5. On the other
hand, nodes located in the important networking hubs of U.S. (e.g, San
Jose, Washington DC, Chicago) have a degree of more than
, which corresponds to an optimal degree of 5. On the other
hand, nodes located in the important networking hubs of U.S. (e.g, San
Jose, Washington DC, Chicago) have a degree of more than 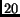 in the
combined topology.
in the
combined topology.


Next: Failure of high connectivity
Up: Geographic fault tolerance of
Previous: Geographic fault tolerance of
Lakshminarayanan Subramanian
2002-04-14

