


Next: Distribution of ISP path
Up: Impact of multiple ISPs
Previous: Impact of path length
Impact of multiple ISPs on circuitousness
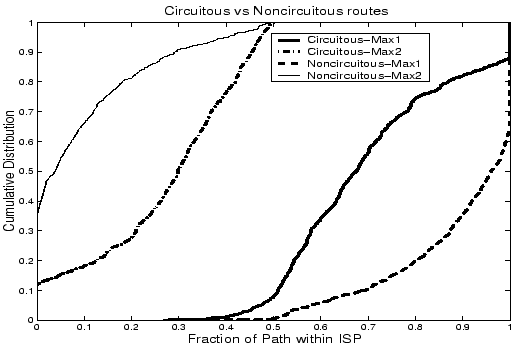
Figure 11:
CDF of the fraction of the end-to-end path that lies within the top 2 ISPs in the case of circuitous paths and non-circuitous paths.
 |
In Section 5.1 we hypothesized that the presence of
multiple ISPs in an end-to-end path contributes to the circuitousness
of the path. We now examine this issue more carefully. We classify
end-to-end paths into two categories - non-circuitous (distance ratio
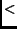 1.5) and circuitous (distance ratio
1.5) and circuitous (distance ratio 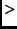 2).7 For each path in either
category, we identify the top two ISPs that account for most of the
end-to-end linearized distance. We then compute the fraction of the
end-to-end linearized distance that is accounted for by the top two
ISPs, and denote these fractions by
2).7 For each path in either
category, we identify the top two ISPs that account for most of the
end-to-end linearized distance. We then compute the fraction of the
end-to-end linearized distance that is accounted for by the top two
ISPs, and denote these fractions by 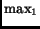 and
and 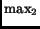 . For example,
if an end-to-end path with a linearized distance of 1000 km traverses
400 km in AT&T's network and 300 km in UUNET's network (and smaller
distances in other networks), then
. For example,
if an end-to-end path with a linearized distance of 1000 km traverses
400 km in AT&T's network and 300 km in UUNET's network (and smaller
distances in other networks), then 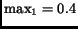 and
and 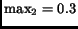 . Note
that it is possible for
. Note
that it is possible for 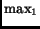 to be 1.0 (and so
to be 1.0 (and so 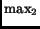 to be 0.0)
if the entire end-to-end path traverses just one ISP network. We note
that local-area networks confined to a city (e.g., a university
network) contribute nil to the linearized distance and therefore are
ignored.
Figure 11 shows the CDF of
to be 0.0)
if the entire end-to-end path traverses just one ISP network. We note
that local-area networks confined to a city (e.g., a university
network) contribute nil to the linearized distance and therefore are
ignored.
Figure 11 shows the CDF of 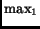 and
and 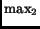 for the circuitous and non-circuitous paths. The difference in the
characteristics of these two categories of paths is striking. The
for the circuitous and non-circuitous paths. The difference in the
characteristics of these two categories of paths is striking. The
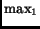 and
and 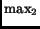 curves are much closer together in the case of
circuitous paths than in the case of non-circuitous paths. In other
words, in the case of circuitous paths, the end-to-end path traverses
substantial distances in each of the top two ISPs (and perhaps other ISPs
too). In contrast, non-circuitous paths tend to be dominated by a
single ISP. For instance, the median values of
curves are much closer together in the case of
circuitous paths than in the case of non-circuitous paths. In other
words, in the case of circuitous paths, the end-to-end path traverses
substantial distances in each of the top two ISPs (and perhaps other ISPs
too). In contrast, non-circuitous paths tend to be dominated by a
single ISP. For instance, the median values of 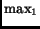 and
and 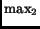 in
the case of circuitous paths is approximately 0.65 and 0.3,
respectively. In other words, the top two ISPs account for 65% and
30%, respectively, of the end-to-end path in the median
case. However, the fractions for the non-circuitous paths are
approximately 95% and 4%, respectively - much more skewed in favor
of the top ISP.
in
the case of circuitous paths is approximately 0.65 and 0.3,
respectively. In other words, the top two ISPs account for 65% and
30%, respectively, of the end-to-end path in the median
case. However, the fractions for the non-circuitous paths are
approximately 95% and 4%, respectively - much more skewed in favor
of the top ISP.
Figure 12:
CDF of the distance ratio as a function of the number of major ISPs traversed along an end-to-end path. There were few paths that traversed more than 3 major ISPs.
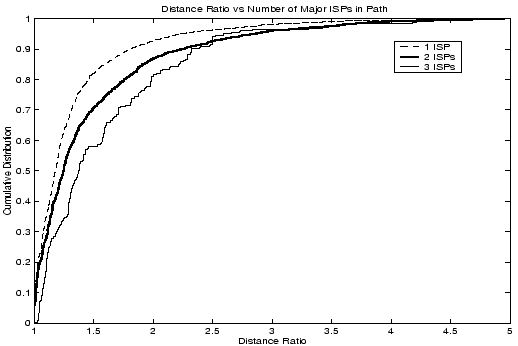 |
We also consider the impact of the number of major ISPs
traversed along an end-to-end path on the distance
ratio. Figure 12 shows a clear trend: the distance ratio
tends to increase as the path traverses a greater number of ISPs. For
instance, the median distance ratios are 1.18, 1.25, and 1.38,
respectively with 1, 2, and 3 major ISPs. The 90th percentile of the
distance ratio is 1.81, 2.26, and 2.35, respectively. A path that
traverses a larger number of major ISPs may span a greater
distance. However, as noted in Section 5.1.1, this
would not explain the larger distance ratio. In fact, a greater
geographic distance would tend to make the distance ratio smaller, not
larger
These findings reinforce our hypothesis that there is a correlation
between the circuitousness of a path (as quantified by the distance
ratio) and the presence or absence of multiple ISPs that account for
substantial portions of the path.


Next: Distribution of ISP path
Up: Impact of multiple ISPs
Previous: Impact of path length
Lakshminarayanan Subramanian
2002-04-14



