


Next: Summary of Results
Up: Circuitousness of Internet paths
Previous: Temporal properties of routing
Correlation between delay and distance
Finally, we analyze the relationship between geography and the end-to-end
delay along a path. Though geography by itself cannot provide any
information about many performance characteristics like bandwidth,
congestion along a path, the linearized distance of a path does
enforce a minimum delay along a path (propagation delay along a path).
To study this correlation, we use the TVHosts data set since it
represents a wide variety of end-hosts. In our traceroute data, we
obtain  RTT samples for every router along the path. Since not all
routers in a path are recognizable, we consider the minimum RTT,
geographic distance and linearized distance to the last recognizable
router along the path. In this analysis, we restrict ourselves to the
list of probes in the U.S.
RTT samples for every router along the path. Since not all
routers in a path are recognizable, we consider the minimum RTT,
geographic distance and linearized distance to the last recognizable
router along the path. In this analysis, we restrict ourselves to the
list of probes in the U.S.
Figure 8:
CDF of minimum end-to-end RTT to TVHosts for different ranges
of linearized distances and geographic distances of paths
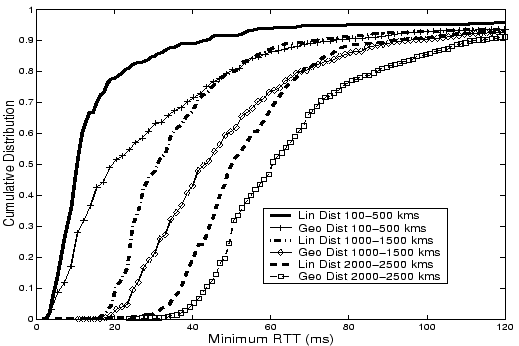 |
Figure 8 illustrates the correlation of the minimum
RTT along a path to the linearized distance of a path and the
geographic distance between the end-hosts. We make three important
observations. First, at low values of the linearized distance there
exists a strong correlation between the delay and linearized distance
for a large fraction of end-hosts especially for small values of
linearized distances. We expect this correlation to be much stronger
as we compute the minimum over a larger number of samples. Second,
linearized distance along a path does enforce a minimum end-to-end RTT
which is an important performance metric for latency sensitive
applications. Third, the minimum RTT between two end-hosts has lesser
correlation to the geographic distance between them as compared to the
linearized distance of the path connecting them. We observe that for a
given range of linearized distance of a path, the RTT variation is
much smaller than its variation for the same range of geographic
distance between the end-hosts. Hence linearized distance of a path
conveys more about the minimum RTT characteristics of a path than
merely the geographic distance between the end-hosts. We also verified
that these observations hold across the other data sets we
collected. The coarse correlation between minimum delay and geographic
distance was used in building GeoPing, an IP-to-location mapping
service [13].


Next: Summary of Results
Up: Circuitousness of Internet paths
Previous: Temporal properties of routing
Lakshminarayanan Subramanian
2002-04-14


