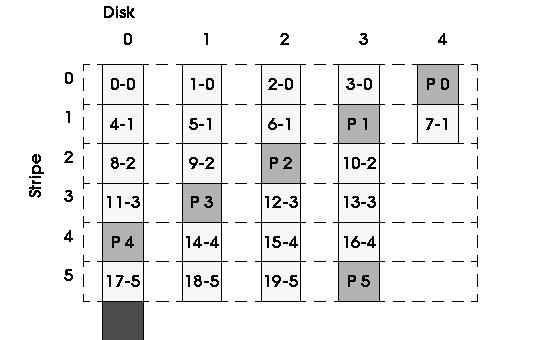
Figure 1: Distribution of data and parity blocks according to the intuitive version.

The intuitive idea is to place more data blocks in the larger disks than in smaller ones. This makes sense when larger disks are also faster, and thus they can serve more blocks per unit of time. Following this idea, we propose to use all D disks (as in a regular RAID5) for as many stripes as blocks can fit in the smallest disk. Once the smallest disk is full, we use the rest of the disks as if we had a disk array with D-1 disks. This distribution continues until all disks are full with data.
A side effect of this distribution is that the system may have stripes with different lengths. For instance, if the array has D disks where F of them are fast, the array will have stripes with D-1 blocks (plus the parity block), but it will also have stripes with F-1 blocks (plus the parity block). This was not a problem in RAIDs level 0 [5], nevertheless, the effect it may have on a RAID 5 will be discussed later in this paper.
Finally, the parity block for each stripe is placed in the same position it would have been in a regular array with as many disks as blocks in the stripe.

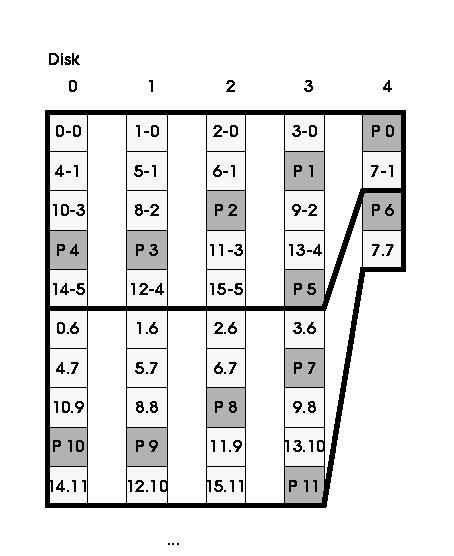
In Figure 1, we present the distribution of blocks in a five-disk array where disks have different capacities. Each block has been labeled with the block number in the array followed by the stripe in which it is located (i.e. 8-2 represents data block 8, which is in the strip number 2). Parity blocks are just labeled with a P and the stripe to which they belong. We have to notice that the last block of the largest disk is not used. This happens because stripes must be at least two blocks long, otherwise there is no room to store the parity block for the stripe.
The solution to this problem can be approached from two different levels: file system or device. In the first case, the file system has to know that there are different stripe sizes in order to optimize writes accordingly. In the second case, which is the one we propose, the array hides the problem from the file system that assumes a fixed stripe size.
The array can hide the problem of having different stripe sizes by making sure that the number of data blocks in each stripe is a divisor of the number of data blocks in the largest stripe, which we assume is what is being used by the file system. This condition guarantees that full stripes, from the file system point of view, are divided into a set of full stripes, and thus the number of small writes is not increased.
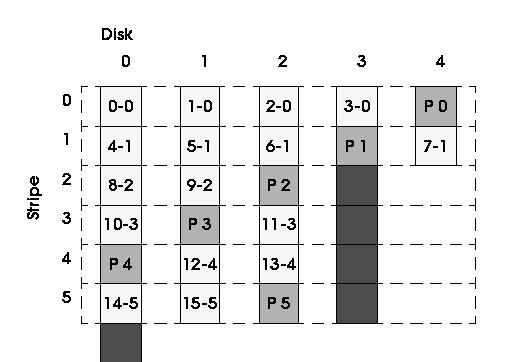
In Figure 2, we present the new distribution for the example in Figure 1. We should notice that the last four blocks in disk 3 become unused. As we have mentioned, the number of data blocks in a stripe has to be a divisor of the data blocks in the largest one. In this example, the largest stripe has 4 data blocks, and thus a stripe with three data blocks is not a valid one. For this reason, stripe number 2 becomes a three-block stripe and all the space in disk 3 that comes after P1 remains unused.
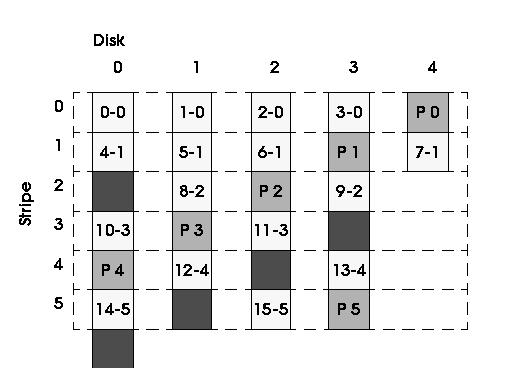
We will describe this optimization in two steps. First, we will find a way to use all the available disks without worrying about the capacity. And second, we will use this distribution to increase the effective capacity.
The first problem, then, is how to map stripes that are N-blocks long in a set of D disks (D > N) using all the disks. One way to do this mapping is to start each stripe in a different disk. For instance, if stripe i starts in disk d, then stripe i+1 should start on disk d-1. Figure 3 shows an example where stripes that are 3-blocks long (2 data plus 1 parity) are distributed among four disks. Please notice that this only happens for stripes 2 to 5.
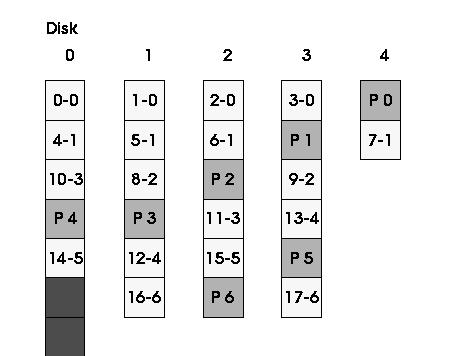
The previous step uses all disks, but the number of unused blocks is not reduced at all. To fill these unused blocks we can use a Tetris-like algorithm. We can push all blocks so that all empty spaces are filled. Figure 4 presents the previous example once the pushing has been done. We can observe now, that all the blocks in the disk are used regardless of the size of the stripe (2 additional data blocks plus one parity block can be accommodated). With this algorithm, we can have stripes with different sizes while all the blocks in all disks are used to store either data or parity information.
This can be a problem if our file system tries to place all the blocks of a file together, which is a common practice [13, 14, 19]. This means that a given file may have most of its blocks in the lower part of the address space (long stripes) while another file may have all its blocks in the higher part of the address space (short stripes). Although the global access in the system will be an average, the first file will have a faster access time (more parallelism) while the second one will have a slower access time (less parallelism). For this reason, evenly distributing the location of long and short stripes all over the array will reduce the variance between the accesses in the different portions of the disk array, which we believe is how the storage system should behave.
To make this distribution, we introduce the concept of a pattern of stripes. The algorithm assumes, for a moment, that disks are smaller than they actually are (but with the same proportions in size) and distributes the blocks in this smaller array. This distribution becomes the pattern that is repeated until all disks are full. The resulting distribution has the same number of stripes as the previous version of the algorithm. Furthermore, each disk also has the same number of blocks as in the previous version. The only difference is that short and long stripes are distributed all over the array, which was our objective. An example of this pattern repetition can be seen in Figure 5.
With this solution, we can see the pictures presented so far (Figures 1, 2, or 4) as patterns that can be repeated in disks thousands of times larger than the ones presented.
It is also important to notice that the concept of patterns will simplify the algorithm to find a block as will be described later (Section 4.2).
In a regular disk array, all stripes are aligned to a multiple of the number of data blocks in the stripe. We may have systems, or applications, that try to align their full-stripe requests to the beginning of a stripe to avoid making extra read operations. For example, if we have a distribution where the pattern is the one in Figure 4, accessing 4 blocks starting from block 16 should be a full stripe. However, it is not with our new block-distribution algorithm.
Before presenting the solution, we need to define the concept of reference stripe. A reference stripe is the stripe that the system or application assumes to be a full stripe. For instance, in the previous example the reference stripe has 4 data blocks and 1 parity block.
The solution to this problem is quite simple. The algorithm only has to make sure that the number of data blocks in a pattern is a multiple of the number of blocks in the reference stripe. This condition guarantees that all repetitions of the pattern start at the beginning of a file system full stripe. The result of applying this last step in the example can be seen in Figure 5.
If we examine the algorithm we can see that there are two main ideas that can be parameterized. The first one is the number of blocks we place in each disk. So far, we assumed that all blocks in a disk are to be used. Now, we want to add a parameter to the algorithm that defines the proportion of blocks that are placed in each disk. The utilization factor (UF), which is defined on a per-disk basis, is a number between 0 and 1 that defines the relationship between the number of blocks placed in each disk. The disk with the most blocks always has a UF of 1 and the rest of disks have a UF related to the number of blocks they use compared to the most loaded one. For instance, if a disk has a UF of 0.5, it means that it stores half the number of blocks as compared to the most loaded one. This parameter allows the system administrator to decide the load of the disks. We can set values that reflect the size of the disks, or we can find values that reflect the performance of the disk instead of the capacity.
The second parameter is the number of stripes in the pattern (SIP). The number of stripes in the pattern indicates how well distributed are the different kinds of stripes along the array. Nevertheless, we should keep in mind that smaller disks will participate in less than SIP stripes.
Figure 5 presents a graphic example of how blocks are distributed in the first two repetitions of the pattern if we use the following parameters: UF0=UF1=UF2=UF3=1, UF4=0.4 and SIP = 6. Please note that there are no empty blocks in the picture because we assume much larger disks and the empty blocks would be placed at the end. Remember that the picture only shows the first two repetitions of the pattern.
This is done in a very simple way. When the system boots, the distribution
of blocks in a pattern is computed and kept in three tables. The first
one (location) contains the disk and position within that disk
of any block in the pattern. The second one (parity) keeps the
location of the parity block for each stripe. Finally, the third table
(Blks_per_disk_in_pattern) stores the number of blocks each disk
has in a pattern. These tables should not be too large. In our experiments
the position table has 152 entries, the parity one only
has 19 entries, and the Blks_per_disk_in_pattern has 9 entries.
These sizes can be assumed by any RAID controller or file system. The formulas
to compute the location of a given block (B) follow:
| disk (B) = location[B % Blks_in_a_pattern].disk | |
| pos (B) = location[B % Blks_in_a_pattern].pos + | |
| (B / Blks_in_a_pattern)* Blks_per_disk_in_pattern[disk(B)] | (1) |
As these operations are very simple, the algorithm to locate blocks
is very fast. To check this time, we profiled the simulator and we found
that the time spent in deciding the location of blocks was less than 81µs
in average per request
![]()
![]()
![]()
![]()
![]()