
15th USENIX Security Symposium
Pp. 193–208 of the Proceedings


Rule-Based Static Analysis of Network Protocol Implementations
Octavian Udrea, Cristian Lumezanu, and Jeffrey S. Foster
{udrea, lume, jfoster}@cs.umd.edu
University of Maryland, College Park
Abstract:
Today's software systems communicate over the Internet using
standard protocols that have been heavily scrutinized, providing
some assurance of resistance to malicious attacks and general
robustness. However, the software that implements those protocols
may still contain mistakes, and an incorrect implementation could
lead to vulnerabilities even in the most well-understood protocol.
The goal of this work is to close this gap by introducing a new
technique for checking that a C implementation of a protocol matches
its description in an RFC or similar standards document. We present
a static (compile-time) source code analysis tool called Pistachio
that checks C code against a rule-based specification of its
behavior. Rules describe what should happen during each round of
communication, and can be used to enforce constraints on ordering
of operations and on data values.
Our analysis is not guaranteed sound due to some heuristic
approximations it makes, but has a low false negative rate in
practice when compared to known bug reports. We have applied
Pistachio to implementations of SSH and RCP, and our system was able
to find many bugs, including
security vulnerabilities, that we confirmed by hand and checked
against each project's bug databases.
1 Introduction
Networked software systems communicate using protocols
designed to provide security against attacks and robustness against
network glitches. There has been a significant body of research, both
formal and informal, in scrutinizing abstract protocols and proving
that they meet certain reliability and safety requirements [24,18,6,14,25]. These abstract protocols, however,
are ultimately implemented in software, and an incorrect
implementation could lead to vulnerabilities even in the most
heavily-studied and well-understood protocol.
In this paper we present a tool called Pistachio that helps close this
gap. Pistachio is a static (compile-time) analysis tool that can
check that each communication step taken by a protocol implementation
matches an abstract specification. Because it starts from a
detailed protocol specification, Pistachio is able to check
communication properties that generic tools such as buffer overflow
detectors do not look for. Our static analysis algorithm is also very
fast, enabling Pistachio to be deployed regularly during the
development cycle, potentially on every compile.
The input to our system is the C source code implementing the protocol
and a rule-based specification of its behavior, where each rule
describes what should happen in a ``round'' of communication. For
example, the IETF current draft of the SSH connection protocol
specifies that ``When either party wishes to terminate the channel, it
sends SSH_MSG_CHANNEL_CLOSE. Upon receiving this message,
a party must send back a
SSH_MSG_CHANNEL_CLOSE .''
This statement translates into the
following rule (slightly simplified): .''
This statement translates into the
following rule (slightly simplified):
This rule means that after seeing a call to recv() whose
second argument points to memory containing
SSH_MSG_CHANNEL_CLOSE, we should reply with the same type
of message. The full version of such a rule would also require that
the reply contain the same channel identifier as the initial
message.
In addition to this specification language,
another key contribution of Pistachio is a novel static analysis
algorithm for checking protocol implementations against their
rule-based specification. Pistachio performs an abstract
interpretation [10] to simulate the execution of
program source code, keeping track of the state of program variables
and of ghost variables representing abstract protocol state,
such as the last value received in a communication. Using a fully
automatic theorem prover, Pistachio checks that whenever it encounters a
statement that triggers a rule (e.g., a call to recv), on all
paths the conclusion of the rule is eventually satisfied (e.g.,
send is called with the right arguments). Although this
seems potentially expensive, our algorithms run efficiently in
practice because the code corresponding to a round of communication is
relatively compact. Our static analysis is not guaranteed to find all
rule violations, both because it operates on C, an unsafe language, and because
the algorithm uses some heuristics to improve performance. In
practice, however, our system missed less than 5% of known bugs when measured
against a bug database.
We have applied Pistachio to two protocol implementations: the LSH
implementation of SSH2 and the RCP implementation from Cygwin.
Analysis took less than a minute for each of the test runs, and
Pistachio detected a multitude of bugs in the implementations,
including many security vulnerabilities. For example, Pistachio
found a known problem in LSH that causes it to leak privileged
information [22].
Pistachio also found a number of buffer overflows due to rule
violations, although Pistachio does not detect arbitrary buffer
overflows.
We confirmed the bugs we found against bug databases for the
projects, and we also found two new unconfirmed security bugs in LSH: a
buffer overflow and an incorrect authentication failure message when
using public key authentication.
In summary, the main contributions of this work are:
- We present a rule-based specification language for describing
network protocol implementations. Using pattern matching to identify routines in
the source code and ghost variables to track state, we can naturally
represent the kinds of English specifications made in documents like
RFCs. (Section 2)
- We describe a static analysis algorithm for checking that an
implementation meets a protocol specification. Our approach uses
abstract interpretation to simulate the execution of the program and
an automatic theorem prover to determine whether the rules are
satisfied. (Section 3)
- We have applied our implementation, Pistachio, to LSH and RCP.
Pistachio discovered a wide variety of known bugs,
including security vulnerabilities, as well as two new unconfirmed bugs.
Overall Pistachio missed about 5% of known bugs and had a 38%
false positive rate. (Section 4)
Based on our results, we believe that Pistachio can be a valuable tool
in ensuring the safety and security of network protocol
implementations.
2 Rule-Based Protocol Specification
Figure 1:
Simple alternating bit protocol implementation
0. int main(void) {
1. int sock, val = 1, recval;
2. send(sock, &val, sizeof(int));
3. while(1) {
4. recv(sock, &recval, sizeof(int));
5. if (recval == val)
6. val += 2;
7. send(sock, &val, sizeof(int));
8. }
9. } |
|
Figure 2:
Rule-based protocol specification
 |
The first step in using Pistachio is developing a rule-based protocol
specification, usually from a standards document. As an example,
we develop a specification for a
straightforward extension of the alternating bit protocol [4]. Here is a
straw-man description of the protocol:
The protocol begins with the current party sending the value  .
In each round, if .
In each round, if
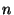 is received then the current party sends is received then the current party sends 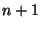 ; otherwise the
current party resends ; otherwise the
current party resends 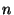 . .
Figure 1 gives a sample implementation of this protocol.
Here recv() and send() are used to receive and send
data, respectively. Notice that this implementation is actually
flawed--on statement 6, val is incremented by 2 instead of by 1.
To check this protocol, we must first identify the communication
primitives in the source code. In this case we see that
the calls to send() in statements 2 and 7 and the call to
recv() in statement 4 perform the communication. More
specifically, we observe that we will need to track the value of the
second argument in the calls, since that contains a pointer to the
value that is communicated.
We use patterns to match these function calls or other
expressions in the source code. Patterns contain pattern
variables that specify which part of the call is of interest to the
rule. For this protocol, we use pattern send(_, out, _) to bind pattern
variable out to the second argument of send(), and
we use pattern recv(_, in, _) to bind in to the second argument
of recv(). For other implementations we may need to use
patterns that match different functions. Notice that in both of these
patterns, we are already abstracting away some implementation details.
For example, we do not check that the last parameter matches the size
of val, or that the communication socket is correct, i.e.,
these patterns will match calls even on other sockets.
Patterns can be used to match any function calls. For example, we
have found that protocol implementers often create higher-level
functions that wrap send and receive operations, rather than calling
low-level primitives directly. Using patterns to match these
functions can make for more compact rules that are faster to check,
though this is only safe if those routines are trusted.
Once we have identified the communication operations in the source
code, we need to write rules that encode the steps of the protocol.
Rules are of the form
where  is a
hypothesis and is a
hypothesis and  is a conclusion, is a conclusion, 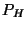 and and 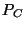 are patterns, and
are patterns, and 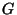 is a set of assignments to ghost variables
representing protocol state. In words, such a rule means: If we find a statement is a set of assignments to ghost variables
representing protocol state. In words, such a rule means: If we find a statement
 in the program that matches pattern in the program that matches pattern 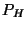 , assume that , assume that  holds,
and make sure that on all possible execution paths from holds,
and make sure that on all possible execution paths from  there is some
statement matching there is some
statement matching 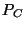 , and moreover at that point the conditions in , and moreover at that point the conditions in
 must hold. If a rule is satisfied in this manner, then the side
effects must hold. If a rule is satisfied in this manner, then the side
effects 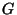 to ghost variables hold after the statements matching to ghost variables hold after the statements matching 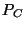 . .
For example, Figure 2 contains the rules for our
alternating bit protocol. Rule (1) is triggered by the start of the
program, denoted by hypothesis 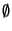 . This rule says that on
all paths from the start of the program, send() must be
called, and its second argument must point to a 4-byte block
containing the value 1. We can see that this rule is satisfied in
statement 2 in Figure 1. As a side effect, the successful
conclusion of rule (1) sets the ghost variable . This rule says that on
all paths from the start of the program, send() must be
called, and its second argument must point to a 4-byte block
containing the value 1. We can see that this rule is satisfied in
statement 2 in Figure 1. As a side effect, the successful
conclusion of rule (1) sets the ghost variable 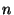 to 1. Thus
the value of to 1. Thus
the value of 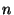 corresponds to the data stored in val.
Notice that there is a call to send() in statement 7 that
could match the conclusion pattern--but it does not,
because we interpret patterns in rules to always mean the first
occurrence of a pattern on a path. corresponds to the data stored in val.
Notice that there is a call to send() in statement 7 that
could match the conclusion pattern--but it does not,
because we interpret patterns in rules to always mean the first
occurrence of a pattern on a path.
Rule (2) is triggered by a call to recv(). It says that if
recv() is called, then assuming that the value 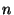 is
received in the first four bytes of is
received in the first four bytes of  , the function send()
must eventually be called with , the function send()
must eventually be called with  as an argument, and as a side
effect the value of as an argument, and as a side
effect the value of 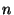 is incremented. Similarly to before, this
rule matches the first occurrence of send() following
recv(). In our example code this rule
is not satisfied. Suppose rule (1) has triggered once, so the value of is incremented. Similarly to before, this
rule matches the first occurrence of send() following
recv(). In our example code this rule
is not satisfied. Suppose rule (1) has triggered once, so the value of
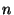 is 1, and we trigger rule (2) in statement 4. Then if we assume is 1, and we trigger rule (2) in statement 4. Then if we assume 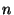 is
received in statement 4, then statement 7 will send is
received in statement 4, then statement 7 will send 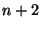 . Hence Pistachio
signals a rule violation on this line. . Hence Pistachio
signals a rule violation on this line.
Finally, rule (3) is triggered on the same call to recv() in
statement 4. It says that if we assume the value of 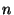 is not received in is not received in
 , then eventually send() is called with , then eventually send() is called with 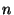 as the
argument. This rule will be satisfied by the implementation, because
when we take the false branch in statement 5 we will resend val,
which always contains as the
argument. This rule will be satisfied by the implementation, because
when we take the false branch in statement 5 we will resend val,
which always contains 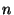 after rules (1) or (3) fire. after rules (1) or (3) fire.
2.2 Developing Rule-Based Specifications
As part of our experimental evaluation
(Section 4), we developed rule-based
specifications for the SSH2 protocol and
the RCP protocol. In both cases we started with a
specification document such as an RFC or IETF standard. We then
developed rules from the textual descriptions in the document,
using the following steps:
- Identifying patterns. The specification writer can either
choose the low-level communication primitives as the primary
patterns, as in Figure 2, or write rules in terms of
higher-level routines. We have attempted both approaches when
developing our specifications, but decided in favor of the first
method for more future portability.
- Defining the rules. The main task in constructing a
rule-based specification is, of course, determining the basic rules.
The specification writer first needs to read the standards document
carefully to discover what data is communicated and how it is
represented. Then to discover the actual rules they should study
the sections of the specification document that describe the
protocol's behavior. We found that phrases containing must
are good candidates for such rules. (For a discussion of terms such
as must, may, and should in RFC documents, see
RFC 1111.)
For instance, as we read the SSH2 standard we learned that the
message format for SSH user authentication starts with the message
type, followed by the user name, service name, and method name.
Furthermore, we found that the use of ``none'' as the authentication
method is strongly discouraged by the specification except for
debugging purposes. This suggested a potential security property:
To prevent anonymous users from
obtaining remote shells, we should ensure that If we receive a
user authentication request containing the none method, we
must return SSH_MSG_USERAUTH_FAILURE. Once we
determine this rule, it is easy to encode it in Pistachio's
notation, given our knowledge of SSH message formats.
- Describing state. Finally, as we are constructing the
rules, we may discover that some protocol steps are state-based.
For instance, in the SSH2 protocol, any banner message
has to be sent before the server sends
SSH_MSG_USERAUTH_SUCCESS. To keep track of whether we
have sent the success message, we introduce a new ghost variable
called successSent that is initially 0 (here we assume for
simplicity that we only have one client). We modify our rules to
set successSent to 1 or 0 in the appropriate cases.
Then the condition on banner messages can be stated as Given
that successSent is 1 and for any message received, the
output message type is different from
SSH_MSG_USERAUTH_BANNER. Our experience is that
coming up with the ghost variables is the least-obvious part of
writing a specification and requires some insight. In the LSH and
RCP protocols, the state of the protocol usually depends on the
previous message that was sent, and so our rules use ghost variables
to track the last message.
Section 4.1 discusses the actual rule-based
specifications we developed for our experiments.
3 Static Analysis of Protocol Source Code
Figure 3:
Static Checking of Example Program
![\includegraphics[height=3in]{cfg2}](img29.png) |
|
Rule (1) |
Hyp: facts = 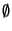 |
|---|
Concl: stmt 2 matches, facts =
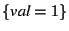 |
|---|
Need to show:
![$\{\textit{val} = 1\} \wedge \{\&\textit{val} = \textit{out}\}
\Rightarrow \textit{out}[0..3] = 1$](img19.png) |
|---|
Action:  |
|---|
|
|
Rule (3) |
|
Hyp: stmt 4 matches, |
|---|
facts =
![$\{n=1, \textit{val}=1, \textit{in}=\textit{\&recval}, \textit{in}[0..3]\neq
n\} = F$](img21.png) |
Branch: Since assumptions
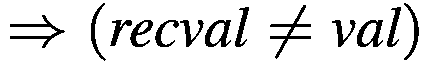 , false branch taken , false branch taken |
|---|
Concl: stmt 7 matches, same facts 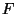 as above as above |
|---|
Need to show:
![$F \wedge \{\textit{\&val}=\textit{out}\} \Rightarrow
\textit{out}[0..3]=n$](img24.png) |
|---|
|
Action: none
|
|---|
|
|
Rule (2) |
|
Hyp: stmt 4 matches, |
|---|
facts =
![$\{n=1, \textit{val}=1, \textit{in}=\textit{\&recval}, \textit{in}[0..3]=n\}$](img25.png) |
Branch: Since assumptions
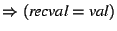 ,
true branch taken ,
true branch taken |
|---|
|
Concl: stmt 7 matches, facts are |
|---|
![$F = \{n=1, \textit{val}=3, \textit{in}=\textit{\&recval}, \textit{in}[0..3]=n\}$](img27.png) |
Need to show:
![$F \wedge \{\textit{\&val}=\textit{out}\} \Rightarrow
(\textit{out}[0..3]=\textit{in}[0..3]+1)$](img28.png) |
|---|
|
Fails to hold; issue warning
|
|---|
|
|
|
(a) Control-Flow Graph |
(b) Algorithm Trace
|
|
Given a set of rules as described in Section 2 and the
source code of a C program, Pistachio performs a static analysis to
check that the program obeys the specified rules.
Pistachio uses abstract interpretation [10] to simulate
the behavior of source code. The basic idea is to associate a set of
facts with each point during execution. In our system, the
facts we need to keep track of are the predicates in the rules and
anything that might be related to them. Each statement in the
program can be thought of as a transfer function [1],
which is a ``fact transformer'' that takes the set of facts
that hold before the statement and determines the facts that
hold immediately after:
- After an assignment statement var = expr, we first
remove any previous facts about var and then add the fact
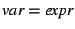 . For example, consider the code in
Figure 1 again. If before statement 6 . For example, consider the code in
Figure 1 again. If before statement 6
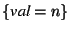 is the set of facts that hold, after the assignment in
statement 6 the set is the set of facts that hold, after the assignment in
statement 6 the set
 holds.
Pointers and indirect assignments are handled similarly, as
discussed below. holds.
Pointers and indirect assignments are handled similarly, as
discussed below.
- If we see a conditional if (p) s1 else s2, we add
the fact that
 holds on the true branch, and that holds on the true branch, and that
 holds on the false branch. For example, in statement 6 in
Figure 1 we can always assume holds on the false branch. For example, in statement 6 in
Figure 1 we can always assume
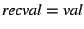 , since to
reach this statement the condition in statement 5 must have been true. , since to
reach this statement the condition in statement 5 must have been true.
- If we see a function call f(x1, ..., xn), we
propagate facts from the call site through the body of f
and back to the caller. I.e., we treat the
program as if all functions are inlined. As discussed below, we
bound the number of times we visit recursive functions to prevent
infinite looping, although recursive functions are rare in practice for
network protocol implementations.
We perform our analysis on a standard control-flow graph (CFG)
constructed from the program source code. In the CFG, each statement
forms a node, and there is an edge from  to to 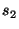 if statement if statement
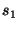 occurs immediately before statement occurs immediately before statement 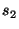 . For example,
Figure 3(a) gives the CFG for the program in Figure 1. . For example,
Figure 3(a) gives the CFG for the program in Figure 1.
Figure 4:
Fact derivation in Pistachio
 |
Figure 4 presents our abstract interpretation
algorithm more formally. The goal of this algorithm is to update
 , a mapping such that , a mapping such that
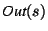 is the set of facts that
definitely hold just after statement is the set of facts that
definitely hold just after statement  . The input to
FactDerivation is an initial mapping . The input to
FactDerivation is an initial mapping  , a set of
starting statements , a set of
starting statements 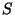 , and a set of ending statements , and a set of ending statements  . The
algorithm simulates the execution of the program from statements in . The
algorithm simulates the execution of the program from statements in
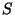 to statements in to statements in  while updating while updating  . Our algorithm
uses an automatic theorem prover to determine which way conditional
branches are taken. In this
pseudocode, we write . Our algorithm
uses an automatic theorem prover to determine which way conditional
branches are taken. In this
pseudocode, we write
 and and
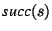 for the predecessor
and successor nodes of for the predecessor
and successor nodes of  in the CFG. in the CFG.
Our simulation algorithm uses a worklist  of statements,
initialized on line 1 of Figure 4. We repeatedly pick
statements from the worklist until it is empty. When we reach a
statement in of statements,
initialized on line 1 of Figure 4. We repeatedly pick
statements from the worklist until it is empty. When we reach a
statement in  on line 6, we stop propagation along that path.
Because the set of possible facts is large (most likely infinite),
simulation might not terminate if the code has a loop. Thus on line 10
we heuristically stop iterating once we have visited a statement on line 6, we stop propagation along that path.
Because the set of possible facts is large (most likely infinite),
simulation might not terminate if the code has a loop. Thus on line 10
we heuristically stop iterating once we have visited a statement
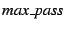 times, where times, where
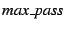 is a predetermined constant bound.
Based on our experiments, we set is a predetermined constant bound.
Based on our experiments, we set
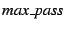 to 75.
We settled on this value empirically by observing that if we vary the
number of iterations, then the overall false positive and false
negative rates from Pistachio rarely changed after 75 iterations in
our experiments. to 75.
We settled on this value empirically by observing that if we vary the
number of iterations, then the overall false positive and false
negative rates from Pistachio rarely changed after 75 iterations in
our experiments.
In line 5 of the algorithm, we compute the set  of facts from
the predecessors of of facts from
the predecessors of  in the CFG. If the predecessor was a
conditional, then we also add in the appropriate guard based on
whether in the CFG. If the predecessor was a
conditional, then we also add in the appropriate guard based on
whether  is on the true or false branch. Then we apply a transfer
function that depends on what kind of statement is on the true or false branch. Then we apply a transfer
function that depends on what kind of statement  is:
Lines 13-15 handle simple assignments, which kill and add facts as
described earlier, and then add successor statements to the worklist.
Lines 16-24 handle conditionals. Here we use an automatic theorem prover to
prune impossible code paths. If the guard is:
Lines 13-15 handle simple assignments, which kill and add facts as
described earlier, and then add successor statements to the worklist.
Lines 16-24 handle conditionals. Here we use an automatic theorem prover to
prune impossible code paths. If the guard  holds in the current
state, then we only add holds in the current
state, then we only add 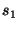 to the worklist, and if to the worklist, and if  holds
then we only add holds
then we only add 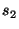 to the worklist. If we cannot prove either,
i.e., we do not know which path we will take, then we add both to the worklist. If we cannot prove either,
i.e., we do not know which path we will take, then we add both 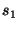 and
and 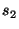 to the worklist.
Finally, lines 25-32 handle function calls. We compute a renaming
map between the actual and formal parameters of to the worklist.
Finally, lines 25-32 handle function calls. We compute a renaming
map between the actual and formal parameters of  ,
and then recursively simulate ,
and then recursively simulate  from its entry node to its
exit nodes. We start simulation in state from its entry node to its
exit nodes. We start simulation in state
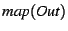 , which contains
the facts in , which contains
the facts in  renamed by renamed by  . Then the
state after the call returns is the intersection of the states at all
possible exits from the function, with the inverse mapping . Then the
state after the call returns is the intersection of the states at all
possible exits from the function, with the inverse mapping
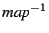 applied. applied.
C includes a number of language features not covered in
Figure 4. Pistachio uses CIL [26] as a front-end, which
internally simplifies many C constructs by introducing temporary
variables and translating loops into canonical form.
We unroll loops up to
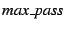 times in an
effort to improve precision. However, as discussed in
Section 3.2, we attempt to find a fixpoint during
unrolling process and stop if we can do so, i.e., if we can find a
loop invariant.
C also includes pointers and a number of
unsafe features, such as type casts and unions. Pistachio tracks
facts about pointers during its simulation, and all C data is modeled
as arrays of bytes with bounds information. When there is an indirect
assignment through a pointer, Pistachio only derives a fact if the
theorem prover can show that the write is within bounds, and otherwise
kills all existing facts about the array. Note that even though a
buffer overflow may modify other memory, we do not kill other facts,
which is unsound but helps reduce false positives. Since all C
data is represented as byte arrays, type casts are implicitly handled
as well, as long we can determine at analysis time the allocation size
for each type, which Pistachio could always do in our experiments. In
addition, in order to reduce false positives Pistachio assumes that variables are initialized with their default values independently of their scope.
In the next sections, we illustrate the use of FactDerivation
during the process of checking the alternating bit protocol from
Figure 2. times in an
effort to improve precision. However, as discussed in
Section 3.2, we attempt to find a fixpoint during
unrolling process and stop if we can do so, i.e., if we can find a
loop invariant.
C also includes pointers and a number of
unsafe features, such as type casts and unions. Pistachio tracks
facts about pointers during its simulation, and all C data is modeled
as arrays of bytes with bounds information. When there is an indirect
assignment through a pointer, Pistachio only derives a fact if the
theorem prover can show that the write is within bounds, and otherwise
kills all existing facts about the array. Note that even though a
buffer overflow may modify other memory, we do not kill other facts,
which is unsound but helps reduce false positives. Since all C
data is represented as byte arrays, type casts are implicitly handled
as well, as long we can determine at analysis time the allocation size
for each type, which Pistachio could always do in our experiments. In
addition, in order to reduce false positives Pistachio assumes that variables are initialized with their default values independently of their scope.
In the next sections, we illustrate the use of FactDerivation
during the process of checking the alternating bit protocol from
Figure 2.
3.1 Checking a Single Rule
Figure 5:
Algorithm for checking a single rule
 |
Given the FactDerivation algorithm, we can now present our
algorithm for checking that the code obeys a single rule  of the form of the form
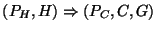 . Assume that we are given a set of
statements . Assume that we are given a set of
statements 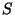 that match that match 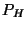 . Then to check . Then to check  , we need to
simulate the program forward from the statements in , we need to
simulate the program forward from the statements in 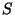 using
FactDerivation. We check that we can reach statements
matching using
FactDerivation. We check that we can reach statements
matching 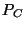 along all paths and that the conclusion along all paths and that the conclusion  holds at those
statements. Figure 5 gives our formal algorithm
Check-SingleRule for carrying out this process. holds at those
statements. Figure 5 gives our formal algorithm
Check-SingleRule for carrying out this process.
The input to CheckSingleRule is a rule  , an initial set of facts , an initial set of facts
 , and a set of starting statements , and a set of starting statements 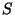 . For all statements
in . For all statements
in 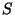 , on line 3 we add to their facts the assumptions , on line 3 we add to their facts the assumptions  and any facts
derived from pattern-matching and any facts
derived from pattern-matching 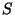 against against 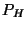 ; we denote this latter
set of facts by ; we denote this latter
set of facts by 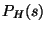 . If there is some path from . If there is some path from 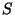 along which we
cannot find a match to along which we
cannot find a match to 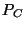 , we report an error on line 5 and consider the rule
unsatisfied. Otherwise on line 6 we search forward along all program
paths until we first find the conclusion pattern , we report an error on line 5 and consider the rule
unsatisfied. Otherwise on line 6 we search forward along all program
paths until we first find the conclusion pattern 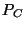 . Then on line
7 we perform abstract interpretation using FactDerivation
to update . Then on line
7 we perform abstract interpretation using FactDerivation
to update  . On line 8, we use the theorem prover to
check whether the
conclusion . On line 8, we use the theorem prover to
check whether the
conclusion  holds at the statements that match holds at the statements that match 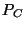 . If they do
then the rule is satisfied, and lines 11-12 update . If they do
then the rule is satisfied, and lines 11-12 update
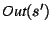 with facts for ghost variables. We
also remove any facts about pattern variables
(in and out in our examples) from with facts for ghost variables. We
also remove any facts about pattern variables
(in and out in our examples) from  (line 14).
(line 14).
We illustrate using CheckSingleRule to check rule (1) from
Figure 2 on the code in Figure 1. The first block in Figure 3(b)
lists the steps taken by the algorithm. We will discuss the remainder
of this figure in Section 3.2.
In rule (1), the hypothesis pattern 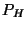 is the start of the program,
and the set of assumptions is the start of the program,
and the set of assumptions  is empty. The conclusion is empty. The conclusion  of this
rule is of this
rule is ![$out[0..3]=1$](img59.png) , where , where  matches the second argument
passed to a call to send(). Thus to satisfy this rule, we
need to show that matches the second argument
passed to a call to send(). Thus to satisfy this rule, we
need to show that ![$out[0..3]=1$](img59.png) at statement 2 in
Figure 1. We begin by adding at statement 2 in
Figure 1. We begin by adding  and and 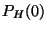 , which in
this case are empty, to , which in
this case are empty, to
 , the set of facts at the
beginning of the program, which is also empty. We trace the program from
this point forward using FactDerivation. In particular, , the set of facts at the
beginning of the program, which is also empty. We trace the program from
this point forward using FactDerivation. In particular,
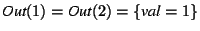 . At statement 2 we match the
call to send() against . At statement 2 we match the
call to send() against  , and thus we also have fact , and thus we also have fact
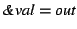 . Then we ask the theorem prover to show . Then we ask the theorem prover to show
 . In this case the proof succeeds,
and so the rule is satisfied, and we set ghost variable . In this case the proof succeeds,
and so the rule is satisfied, and we set ghost variable 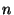 to 1. to 1.
3.2 Checking a Set of Rules
Figure 6:
Algorithm for checking a set of rules
 |
Finally, we develop our algorithm for checking a set of rules.
Consider again the rules in Figure 2. Notice that rules
(2) and (3) both depend on 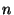 , which is set in the
conclusion of rules (1) and (2). Thus we need to check whether rules
(2) or (3) are triggered on any program path after we update , which is set in the
conclusion of rules (1) and (2). Thus we need to check whether rules
(2) or (3) are triggered on any program path after we update 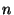 , and
if they are, then we need to check whether they are satisfied. Since
rule (2) depends on itself, we in fact need to iterate.
Formally, we say that rule , and
if they are, then we need to check whether they are satisfied. Since
rule (2) depends on itself, we in fact need to iterate.
Formally, we say that rule 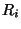 depends on rule depends on rule
 if if  sets a ghost variable that sets a ghost variable that 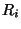 uses in its
hypothesis. We can think of dependencies as defining a graph between
rules, and we use a modified depth-first search algorithm to check
rules in the appropriate order based on dependencies. uses in its
hypothesis. We can think of dependencies as defining a graph between
rules, and we use a modified depth-first search algorithm to check
rules in the appropriate order based on dependencies.
Figure 6 gives our algorithm for checking a set of
rules. The input is a set of rules  that need to
be checked, a mapping that need to
be checked, a mapping  of facts at each program point, and a
set of statements of facts at each program point, and a
set of statements 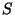 from which to begin checking the rules in from which to begin checking the rules in  .
To begin checking the program, we call .
To begin checking the program, we call
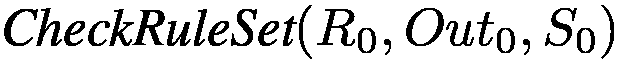 , where , where 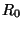 is the rule with hypothesis is the rule with hypothesis 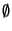 (we
can always create such a rule if it does not exist), (we
can always create such a rule if it does not exist),  is the
initial statement in the program, and is the
initial statement in the program, and 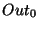 maps every statement to
the set of all possible facts. maps every statement to
the set of all possible facts.
Then the body of the algorithm removes a rule  from the worklist from the worklist  and
checks it. Because rule dependencies may be cyclic, we may visit a
rule multiple times, and as in Figure 5 we terminate
iteration once we have visited a rule and
checks it. Because rule dependencies may be cyclic, we may visit a
rule multiple times, and as in Figure 5 we terminate
iteration once we have visited a rule
 times (line 5). On line 8 we
trace forward from times (line 5). On line 8 we
trace forward from 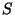 to find all statements to find all statements  that match that match 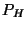 .
Then we copy the current set of facts .
Then we copy the current set of facts  into a new set into a new set
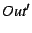 , simulate the program from , simulate the program from 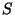 to to  (line 10), and then on line 11
check the rule (line 10), and then on line 11
check the rule  with facts with facts 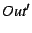 . Notice that the call to
FactDerivation on line 10 and the call to
CheckSingleRule on line 11 modify the copy . Notice that the call to
FactDerivation on line 10 and the call to
CheckSingleRule on line 11 modify the copy 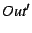 while
leaving the original input while
leaving the original input  unchanged. This means that in
the next iteration of the loop, when we pick another rule from the
worklist and check it starting from unchanged. This means that in
the next iteration of the loop, when we pick another rule from the
worklist and check it starting from 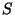 , we will again check it
using the initial facts in , we will again check it
using the initial facts in  , which is the intended behavior:
A call to CheckRuleSet should check all rules in , which is the intended behavior:
A call to CheckRuleSet should check all rules in  starting
in the same state. Finally, on line 14, if the rule starting
in the same state. Finally, on line 14, if the rule  was
satisfied, we compute the set of all rules that depend on was
satisfied, we compute the set of all rules that depend on  , and
then we recursively check those rules, starting in our new state from
statements that matched the conclusion pattern. , and
then we recursively check those rules, starting in our new state from
statements that matched the conclusion pattern.
We illustrate the algorithm by tracing through the remainder of
Figure 3(b), which describes the execution of
CheckRuleSet on our example program. Observe that rule (1)
can be checked with no assumptions, hence we use it to begin the
checking process. We begin with the initial statement in the program
and call CheckSingleRule. As described in
Section 3.1, we satisfy rule (1) at statement 2,
and we set ghost variable 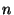 to 1. Thus after checking rule (1), we
can verify rules that depend on to 1. Thus after checking rule (1), we
can verify rules that depend on 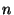 's value. For our example, either
rule (2) or rule (3) might fire next, and so 's value. For our example, either
rule (2) or rule (3) might fire next, and so  will contain both of
them. will contain both of
them.
Suppose we next choose rule (3). We
continue from statement 2, since that is where we set ghost variable
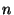 , and we perform abstract interpretation forward until we find a
statement that matches the hypothesis pattern of rule (3), which is
statement 4. Now we add the hypothesis assumption , and we perform abstract interpretation forward until we find a
statement that matches the hypothesis pattern of rule (3), which is
statement 4. Now we add the hypothesis assumption
![$\textit{in}[0..3] \neq n$](img76.png) to our
set of facts and continue forward. When we reach statement 5, the theorem
prover shows that the false branch will be taken, so we only continue
along that one branch--which is important, because if we followed the
other branch we would not be able to prove the conclusion. Taking the
false branch, we fall through to statement 7, and the theorem prover
concludes that rule (3) holds. to our
set of facts and continue forward. When we reach statement 5, the theorem
prover shows that the false branch will be taken, so we only continue
along that one branch--which is important, because if we followed the
other branch we would not be able to prove the conclusion. Taking the
false branch, we fall through to statement 7, and the theorem prover
concludes that rule (3) holds.
Once we are done checking rule (3),
we need to go back and start checking rule (2) where we left off after
rule (1), namely just after we set  after statement 2. The set of
facts contains after statement 2. The set of
facts contains  and and
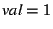 , both set during the checking of rule
(1). We continue forward from statement 2, match the hypothesis of rule (2)
at statement 4, and then this time at the conditional we conclude that the true
branch is taken, hence , both set during the checking of rule
(1). We continue forward from statement 2, match the hypothesis of rule (2)
at statement 4, and then this time at the conditional we conclude that the true
branch is taken, hence  becomes 3 at statement 7. Now the
conclusion of the rule cannot be proven, so we issue a
warning that the protocol was violated at this statement. becomes 3 at statement 7. Now the
conclusion of the rule cannot be proven, so we issue a
warning that the protocol was violated at this statement.
Suppose for illustration purposes
that rule (2) had checked successfully, i.e., in statement 6, val
was only incremented by one. Then at statement 7 we would have shown the
conclusion and set ghost variable
![$n:=\textit{out}[0..3]$](img79.png) . Then since we
changed the value of . Then since we
changed the value of 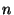 , we need to re-check rules (2) and (3)
starting from this point, since they depend on the value of , we need to re-check rules (2) and (3)
starting from this point, since they depend on the value of 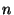 . Of
course, if we follow the loop around again we would need to check
rules (2) and (3) yet again, leading to an infinite loop, cut off
after max_pass times. . Of
course, if we follow the loop around again we would need to check
rules (2) and (3) yet again, leading to an infinite loop, cut off
after max_pass times.
In order to model this case more efficiently, Pistachio's
implementation of CheckRuleSet includes a technique for
finding a fixpoint and safely stopping abstract interpretation early.
Due to lack of space, we omit pseudocode for this technique and
illustrate it by example.
During the first check of rule (2), we would have that
 , where the superscript of , where the superscript of  indicates
how many iterations we have performed. After rule (2) succeeds at
statement 7, we set indicates
how many iterations we have performed. After rule (2) succeeds at
statement 7, we set 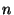 to to  , and hence , and hence
 .
Since rule (2) depends on itself, we need to check it once again. After
simulating the loop in statements 3-8 another time, we would
check rule (2) with facts .
Since rule (2) depends on itself, we need to check it once again. After
simulating the loop in statements 3-8 another time, we would
check rule (2) with facts
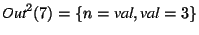 . Rather than
continuing until we reach . Rather than
continuing until we reach
 , we instead try to intersect the facts we have
discovered to form a potential loop invariant. We look at the set of
facts that hold just before rule (2) is triggered and just after rule
(2) is verified: , we instead try to intersect the facts we have
discovered to form a potential loop invariant. We look at the set of
facts that hold just before rule (2) is triggered and just after rule
(2) is verified:
 |
Initial entry to loop |
 |
Back-edge from the first iteration |
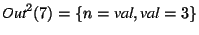 |
Back-edge from the second iteration |
Generally speaking, at step  we are interested in the intersection we are interested in the intersection
![$\textit{Out}^0(2)\cap\bigcap_{i\in[1,k]}\textit{Out}^i(7)$](img84.png) . In our case, the only fact in
this intersection is . In our case, the only fact in
this intersection is
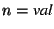 . We then set . We then set
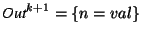 (thus
ignoring the particular value of (thus
ignoring the particular value of  for step for step  ) and attempt to
verify rule (2) once more. Rule (2) indeed verifies, which means we
have reached a fixpoint, and we can stop iterating well before
reaching max_pass. We found this technique for finding fixpoints
effective in our experiments (Section 4). ) and attempt to
verify rule (2) once more. Rule (2) indeed verifies, which means we
have reached a fixpoint, and we can stop iterating well before
reaching max_pass. We found this technique for finding fixpoints
effective in our experiments (Section 4).
4 Implementation and Experiments
Our tool Pistachio is implemented in approximately 6000 lines of OCaml.
We use CIL [26] to parse C programs and Darwin [5] as
the automated theorem prover. Darwin is a sound,
fully-automated theorem prover for first order clausal logic. We
chose Darwin because it performs well and can handle the limited set
of Horn-type theorems we ask it to prove. Since Darwin is not
complete, it can return either ``yes,'' ``no,'' or ``maybe'' for each
theorem. Pistachio conservatively assumes that a warning should be
generated if a rule conclusion cannot be provably implied by
the facts derived starting from the hypothesis.
Figure 7:
Categorization and example rules for the SSH2 protocols
![\begin{figure*}\scriptsize \centering \begin{displaymath}
\begin{array}{\vert l...
... flag [byte 15] set to 1.}\\ \hline
\end{array} \end{displaymath} \end{figure*}](img87.png) |
In order to analyze realistic programs, Pistachio needs to model system
libraries.
When Pistachio encounters a library call, it generates a skeleton
rule-based specification for the function that can be filled in by the
user. Rules for library functions are assumed correct, rather
than checked. For our experiments we added such specifications for several
I/O and memory allocation routines. There are some
library functions we cannot fully model in our framework, e.g.,
 , which potentially depends on any other library
call. In this case, Pistachio assumes that conditionals based on the
result of , which potentially depends on any other library
call. In this case, Pistachio assumes that conditionals based on the
result of
 may take either branch, which can
reduce precision. may take either branch, which can
reduce precision.
4.1 Core Rule Sets
We evaluated Pistachio by analyzing the
LSH [21]
implementation of SSH2 and the RCP implementation from Cygwin's
inetutils package. We chose these systems because of their
extensive bug databases and the number of different versions
available.
We created rule-based specifications by following the process described in
Section 2.2. Our (partial) specification for
SSH2 totaled 96 rules, and the one for RCP totaled 58 rules. Because
the rules describe particular protocol details and are interdependent,
it is difficult to correlate individual rules with general correctness
or security properties. In Figure 7, we give a rough
breakdown of the rules in our SSH2 specification, and we list
example rules with descriptions. These
rules are taken directly from our
experiments--the only changes are that we have reformatted them in
more readable notation, rather than in the concrete grammar used in
our implementation, and we have used send and
recv rather than the actual function names.
The categories we chose are based on functional behavior. The first
category, message structure and data transfer, includes rules
that relate to the format, structure, and restrictions on messages in
SSH2. The example rule requires that any prompt sent to keyboard interactive
clients not be the empty string.
The second category, compatibility rules, includes rules about
backwards compatibility with SSH1. The example rule places a
requirement on sending an identification string in compatibility mode.
The third category, functionality rules, includes rules about what
abilities should or should not be supported. The example rule
requires that the implementation not allow the ``none''
authentication method.
The last
category, protocol logic rules, contains the majority of the rules.
These rules require that the proper response is sent for each received
message. The first example rule requires that the server provide an
adequate response to TCP/IP forwarding requests with a value of 0 for
port. The second rule requires that the server replies to all
global requests that have the wantreply flag set.
Figure 8:
Analysis Results with Core Rule Sets
 |
Based on our experience developing rules for SSH and RCP, we believe
that the process does not require any specialized knowledge other than
familiarity with the rule-based language grammar and the specification
document. It took the authors less than 7 hours to develop each of
our SSH2 and RCP specifications.
The rules are generally
slightly more complex than is shown in Figure 7,
containing on average 11 facts in the hypothesis and 5 facts in the
conclusion for LSH, and 9 facts for the hypothesis and 4 for the
conclusion for RCP. Originally, we started with a rule set derived
directly from specification documents, which was able to catch many
but not all bugs, and then we added some additional rules (a little
over 10% more per specification) to look for some specific known bugs
(Section 4.4). These additional rules produced
about 20% of the warnings from Pistachio. Generally, the rules written
from the specification document tend to catch
missing functionality and message format related problems,
but are less likely to catch errors relating to compatibility problems
or unsafe use of library functions. The process of extending the
initial set of rules proved fairly easy, since specific information
about the targeted bugs was available from the respective bug
databases.
We started with initial specifications for the SSH2 protocols (87 rules) and the RCP protocol
(51 rules), with ``core rules'' based only on specification documents.
In Section 4.4 we discuss extending these rules to target
particular bugs. Using these specifications, we ran our tool against
several different versions of LSH, ranging from 0.1.3 to 2.0.1, and
several different versions of RCP, ranging from 0.5.4 to 1.3.2. We
used the same specification for all versions of the code, and we ran
Pistachio with max_pass set to 75.
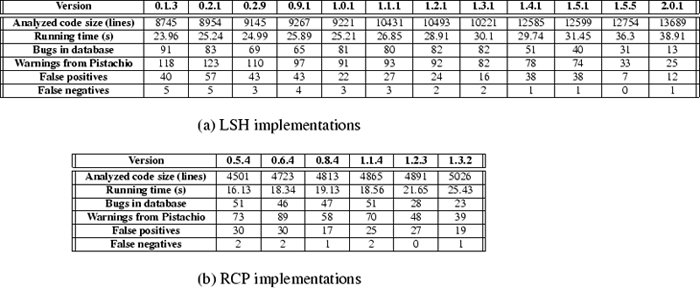
Figure 8 presents the results of our analysis. We
list the lines of code (omitting comments and blank lines) analyzed by
Pistachio. We only include code involved in the rules,
e.g., we omit the bodies of functions our rules treat as
opaque, such as cryptographic functions.
The third row contains the running time of our system. (The
running times include the time for checking the core rules plus the
additional rules discussed in the next section.) In all cases the running times were under one minute.
The next four rows
measure Pistachio's effectiveness. We list the number of bugs found
in the project's bug database for that version and the number of
warnings issued by Pistachio. We counted only bugs in the database
that were reported for components covered by our specifications. For
instance, we only include bugs in LSH's authentication and transport
protocol code and not in its connection protocol code. We also did
not include reports that appeared to be feature requests or other
issues in our bug
counts. The last two rows report the number of false positives
(warnings that do not correspond to bugs in the code) and false
negatives (bugs in the database we did not find).
We found that most of the warnings reported by Pistachio corresponded to
bugs that were in the database. We also found two apparently new bugs
in LSH version 2.0.1. The first involves a buffer overflow in buffers
reserved for passing environment variables in the implementation of
the SSH Transport protocol. The second involves an incorrectly formed
authentication failure message when using PKI. We have not yet
confirmed these bugs; we sent an email to the LSH mailing list with a
report, but it appears that the project has not been maintained
recently, and we did not receive a response.
To determine whether a warning is a bug, we trace the fact derivation
process in reverse, using logs produced by Pistachio that give
 for each analyzed statement. We start from a rule failure
at a conclusion, and then examine the preceding statements to see
whether they directly contradict those facts. If so, then we have
found what we think is a bug, and we look in the bug database to judge
whether we are correct. If the preceding statements do not directly
contradict the facts, we continue tracing backward, using for each analyzed statement. We start from a rule failure
at a conclusion, and then examine the preceding statements to see
whether they directly contradict those facts. If so, then we have
found what we think is a bug, and we look in the bug database to judge
whether we are correct. If the preceding statements do not directly
contradict the facts, we continue tracing backward, using  to help understand the results, until we either find a contradiction
or reach the hypothesis, in which case we have found a false positive.
If the conclusion pattern is not found on all program paths, we use
the same process to determine why those paths were not pruned from the
search during fact derivation.
to help understand the results, until we either find a contradiction
or reach the hypothesis, in which case we have found a false positive.
If the conclusion pattern is not found on all program paths, we use
the same process to determine why those paths were not pruned from the
search during fact derivation.
Figure 9:
Sample compatibility bug
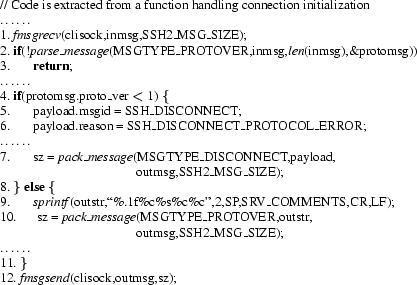 |
As a concrete example of this process, consider the second rule
in Figure 7. This rule is derived from section 5
of the SSH2 Transport Protocol specification, and Pistachio reported
that this rule was violated for LSH implementation 0.2.9, since it
could not prove that
![$\textit{out}[\textit{len}(\textit{out})-2]=\textit{CR}$](img91.png) and and
![$\textit{out}[\textit{len}(\textit{out})-1]=\textit{LF}$](img92.png) at a
conclusion. Figure 9 shows the code (slightly
simplified for readability) where the bug was reported. Statement 12
matches the conclusion pattern (here fmsgsend is a wrapper
around send), and so that is where we begin. Statement 12 has
two predecessors in the CFG, one for each branch of the conditional
statement 4. Looking through the log, we determined that the required
facts to show the conclusion were in at a
conclusion. Figure 9 shows the code (slightly
simplified for readability) where the bug was reported. Statement 12
matches the conclusion pattern (here fmsgsend is a wrapper
around send), and so that is where we begin. Statement 12 has
two predecessors in the CFG, one for each branch of the conditional
statement 4. Looking through the log, we determined that the required
facts to show the conclusion were in
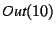 but not in but not in
 . We examined statement 7, and observed that if it is
executed (i.e., if the conditional statement 4 takes the true branch),
then line 10 will send the a disconnect message, which is incorrect.
Thus we backtracked to statement 4 and determined that
protomsg.proto_ver . We examined statement 7, and observed that if it is
executed (i.e., if the conditional statement 4 takes the true branch),
then line 10 will send the a disconnect message, which is incorrect.
Thus we backtracked to statement 4 and determined that
protomsg.proto_ver 1 could not be proved either true or false based
on 1 could not be proved either true or false based
on
 , which was correctly derived from the hypothesis
(asserted in , which was correctly derived from the hypothesis
(asserted in
 ). Thus we determined that we found a bug,
in which the implementation could send an SSH_DISCONNECT
message for clients with versions below 1.0, although the protocol
specifies that the server must send the identification first,
independently of the other party's version. We then confirmed this
bug against the LSH bug database. ). Thus we determined that we found a bug,
in which the implementation could send an SSH_DISCONNECT
message for clients with versions below 1.0, although the protocol
specifies that the server must send the identification first,
independently of the other party's version. We then confirmed this
bug against the LSH bug database.
While it is non-trivial to determine whether the reports issued by
Pistachio correspond to bugs, we found it was generally
straightforward to follow the process described above. Usually the
number of facts we were trying to trace was small (at most 2-3), and
the number of preceding statements was also small (rarely larger than
2). In the vast majority of the cases, it took on the order of
minutes to trace through a Pistachio warning, though in some cases it
took up to an hour (often due to insufficiently specified library
functions that produced many paths). In general, the effort required
to understand a Pistachio warning is directly proportional to the
complexity of the code making up a communication round.
Figure 10:
Error breakdown by type in LSH version 1.2.1
|
Figure 10 gives a more detailed breakdown of our
results on LSH version 1.2.1. We divide the warnings and bugs into
five main categories. The categories mostly but do not completely
correspond to those in Figure 7.
Figure 11:
Sample functionality bug
 |
Functionality errors correspond to missing functionality for
which the implementation does not degrade gracefully, or conversely,
to additional functionality that should not be present. The vast
majority of these bugs were found as violations of rules in the
functionality category from Figure 7.
For example, the third rule in Figure 7
detected a functionality bug in LSH version 0.1.3, for the code in
Figure 11. In this case, a message is received at
statement 2, and Pistachio assumes the rule hypotheses, which indicate
that the message is a user authorization request. Then a success
message is always sent in statement --but the rule specifies that
the ``none'' authentication method must result in a failure response.
Tracing back through the code, we discovered that the else
statement on line 6 allows the ``none'' method to succeed. This
statement should have checked for the ``hostbased'' authentication
method, and indeed this corresponds to a bug in the LSH bug database.
Message format errors correspond to problems with certain
message formats, and are found by violations of the message
format and data transfer rules. For example, the first rule in
Figure 7 detected a violation in LSH version 0.2.9
(code not shown due to lack of space).
In this version of LSH, the server stores the string values of the
possible prompts in an array terminated by the empty string. However,
the implementation uses the array size and not the empty string
terminator to determine the end of the array, which
causes the implementation to potentially include the empty string
terminator as one of the prompts, violating the rule.
Compatibility related errors correspond to problems in the
implementation that cause it to work incorrectly with clients or
servers that implement earlier versions of the SSH protocol. These
bugs correspond to violations of compatibility rules, and the
earlier discussion of the code in Figure 9 illustrated
one example.
Figure 12:
Sample buffer overflow
![\begin{figure}\scriptsize0. ~char laddr[17]; int lport; \\
\ldots\ldots\\
1.~\...
...~~~$\textit{fmsgsend}(clisock,outmsg,sz);\\
14.$~~~~~~$\}\\
15.\}
\end{figure}](img100.png) |
Buffer overflows are detected by Pistachio indirectly during
rule checking. Recall that when Pistachio sees a write to an array
that it cannot prove is in-bounds, then it kills facts about the array.
Thus sometimes when we investigated why a
conclusion was not provable, we discovered it was due to an
out-of-bounds write corresponding to a buffer overflow. For example,
consider the code in Figure 12, which is
taken from LSH version 0.9.1 (slightly simplified). While checking this code,
we found a violation of the fourth rule in Figure 7, as follows. At statement 1, Pistachio
assumes the hypothesis of this rule, including that the
wantreply flag (corresponding to in[15]) is set, and
that the message is for TCP forwarding. Under these assumptions,
Pistachio reasons that the true branch of statement 4 is taken.
But then line 5 performs a strcpy into laddr, which is a
fixed-sized locally-allocated array. The function
getstrfield() (not shown) extracts a string out of the
received message, but that string may be more than 17 bytes.
Thus at the call to strcpy,
there may be a write outside the bounds of laddr, and so we kill facts
about laddr. Then at statement 7, we call
create_forwarding(), which expects laddr to be
null-terminated--and since we do not know whether there is a null
byte within laddr, Pistachio determines that
create_forwarding() might return false, causing us to return
from this code without executing the call to fmsgsend in
statement 13.
In this case, if Pistachio had been able to reason at statement 5 that
laddr was null-terminated, then it would not have issued a warning.
Although the return statement 8 might seem be reachable in that case,
looking inside of create_forwarding(), we find
that can only occur if LSH runs out of ports, and our model
for library functions assumes that this never happens.
(Even if an ill-formed address is passed to
create_forwarding(), it still creates the forwarding for 0.0.0.0.)
On the hand, if create_forwarding() had relied on the length
of laddr, rather than it being null-terminated, then Pistachio would
not have reported a warning here--even though there still would be a
buffer overflow in that case. Thus the ability to detect buffer
overflows in Pistachio is somewhat fragile, and it is a
side effect of the analysis that they can be detected at all. Buffer
overflows that do not result in rule
violations, or that occur in code we do not analyze, will go
unnoticed.
Figure 13:
Sample library call bug
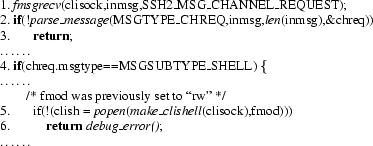 |
Library call errors correspond to unsafe use of library
functions. These bugs are generally found the same ways buffer
overflows are, as a side effect of rule checking. For example,
Figure 13 contains code from LSH 0.9.1 that violated the
last rule in Figure 7. In this case, we matched the
hypothesis of the rule at statement 1, and then matched the request
type at statement 2, and thus one possible path leads to the call to
popen in statement 5. In this case, our model of popen
requires that the second argument must be either ``r'' or ``w,'' or
the call to popen yields an undefined result. Since before
statement 5 fmod was set to ``rw,'' Pistachio assumes that
popen may return any value, including null, and thus
statement 6 may be executed and return without
sending a reply message, thus violating the rule conclusion. Note
that our model of popen always succeeds if valid
arguments are passed, and thus if fmod were ``r'' or ``w'' a
rule violation would not have been reported.
Figure 14:
Causes for false positives in LSH
|
In addition to warnings that correspond to bugs, Pistachio also issues
a number of false positives. Figure 14 breaks down
the causes of false positives found in LSH, averaged over all
versions. The main cause of false positives is insufficient
specification of library calls. This is primarily due to the fact
that library functions sometimes rely on external factors such as
system state (e.g., whether getenv() returns NULL or not depends on which
environment variables are defined)
that cannot be fully modeled using our rule-based semantics. For such
functions, only partial specifications can be devised. The remaining
false positives are due to limitations of the theorem prover and to
loop breaking, where we halt iteration of our algorithm after max_pass
times.
Besides false positives, Pistachio also has false negatives, as measured
against the LSH and RCP bug databases. From our experience, these are
generally caused by either assumptions made when modeling library
calls, or by the fact that the rule sets are not complete. As an
example of the first case, we generally make the simplifying
assumption that on open() calls, there are sufficient file
handles available. This caused a false negative for LSH version
0.1.3, where a misplaced open() call within a loop lead to
the exhaustion of available handles for certain SSH global requests.
4.3 Security Implications
As can be seen from the previous discussion, many of the bugs found by
Pistachio have obvious security implications. Even bugs that initially
appear benign may introduce security vulnerabilities, depending on
what constitutes a vulnerability in a particular circumstance.
However, in order to measure our results we looked through the bug
databases to identify which of the bugs are either clearly
security-related by their nature or were documented as
security-related. On average, we classified approximately 30% of the
warnings (excluding false positives) as security-related for LSH and
approximately 23% for RCP. Of these, buffer overflows account for
approximately 53% of the security-related bugs. We consider all
buffer overflows security-related. Access control warnings account
for 20% of the total. These refer to the execution of functions
for which the user does not have
sufficient privileges. Finally, compatibility problems account for
18% of the total. These do not directly violate security, but
do impede the use of a secure protocol. The remaining
security-related bugs did not fall into any broader categories.
Our classification of bugs as security-related has some uncertainty,
because the bug databases might incorrectly
categorize some non-exploitable bugs as security holes. Conversely,
some bugs that are not documented as being security-related might be
exploitable by a sufficiently clever attacker. In general, any bug in
a network protocol implementation is undesirable.
Figure 15:
Analysis Results for Extended Rule Sets
 |
4.4 Results for Extended Rule Sets
In a second set of experiments, we were interested in estimating how
easily the rule-based specification could be extended to catch
specific bugs we found in the bug databases. Our goal was to study
how Pistachio could be used during the development process. In
particular, as a programmer finds bugs in their code, good software
engineering practice is to write regression tests to catch the bug
again if it appears in the future. In the same way, using Pistachio
the programmer can write extra ``regression rules'' to re-run in the
future.
We looked for bugs we missed using the core set of rules and added
slightly over 10% more rules (9 new rules for LSH and 7
for RCP) to the initial specifications to cover most of the bugs. We
found the rules we needed to add were typically for features that were
strongly recommended but not required by the specification, because it
turned out that violations of these recommendations were considered
errors. One example is the recommendation that a proper
disconnect message be sent by the SSH server when authentication
fails.
Figure 15 shows the effect of the additional
rules on the number of the errors detected. In each table we show the
specific implementation version, the number of bugs in the database,
the total number of warnings from Pistachio and the number of warnings
generated from the 10% additional rules. The last two rows in each
table in Figure 15 contain the number of false
positives caused by the additional rules and the number of false negatives that remain after enriching the specification. We can see that the additional rules account for under 20% of the total number
of warnings generated by Pistachio.
From the set of new warnings produced by Pistachio after
introducing the additional rules, approximately 18% had security
implications according to our classification from
Section 4.3, mostly related to access control
issues and buffer overflows. Roughly half of the remaining false
negatives are due to terminating iteration after max_pass times, and
the other half are due to aspects of the protocol our new rules still
did not cover.
For the extended rules, we also measured how often we are able to
compute a symbolic fixpoint for loops during our analysis. Recall
that if we stop iteration of our algorithm after max_pass times then we
could introduce unsoundness, which accounts for approximately 27% of
the false positives, as shown in Figure 14. We found
that when max_pass is set to 75, we find a fixpoint before reaching
max_pass in 250 out of 271 cases for LSH, and in 153 out of 164 cases
for RCP. This suggests that our symbolic fixpoint computation is
effective in practice.
5 Related Work
Understanding the safety and robustness of network protocols is
recognized as an important research area, and the last decade has
witnessed an emergence of many techniques for verifying protocols.
We are aware of only a few systems that, like Pistachio, directly
check source code rather than abstract models of
protocols. CMC [24] and VeriSoft [15] both model
check C source code by running the code dynamically on hardware, and
both have been used to check communication protocols. These systems
execute the code in a simulated environment in which the model checker
controls the execution and interleaving of processes, each of which
represents a communication node. As the code runs, the model checker
looks for invalid states that violate user-specified assertions, which
are similar to the rules in Pistachio. CMC has been successfully used
to check an implementation of the AODV routing protocol [24] and
the Linux TCP/IP protocol [23].
There are two main drawbacks to these approaches. First, they
potentially suffer from the standard state space explosion problem of
model checking, because the number of program executions and
interleavings is extremely large. This is
typical when model checking is used for data dependent properties, and
both CMC and VeriSoft use various techniques to limit their search.
Second, these tools find errors only if they actually occur during
execution, which depends on the number of simulated processes and on
what search algorithm is used. Pistachio makes different tradeoffs.
Because we start from a set of rules describing the protocol, we need
only perform abstract interpretation on a single instance of the
protocol rather than simulating multiple communication nodes, which
improves performance. The set of rules can be refined over time to find
known bugs and make sure that they do not appear again. We search for errors by program source path
rather than directly in the dynamic execution space, which means that
in the best case
we are able to use symbolic information in the dataflow facts to
compute fixpoints for loops, though in the worst case we unsafely
cut off our search after
 iterations. Pistachio is also very
fast, making it easy to use during the development process.
On the other hand, Pistachio's rules cannot enforce the general kinds
of temporal properties that model checking can.
We believe that
ultimately the CMC and VeriSoft approach and the Pistachio approach
are complementary, and both provide increased assurance of the safety
of a protocol implementation. iterations. Pistachio is also very
fast, making it easy to use during the development process.
On the other hand, Pistachio's rules cannot enforce the general kinds
of temporal properties that model checking can.
We believe that
ultimately the CMC and VeriSoft approach and the Pistachio approach
are complementary, and both provide increased assurance of the safety
of a protocol implementation.
Other researchers have proposed static analysis systems that have been
applied to protocol source code. MAGIC [7] extracts a finite
model from a C program using various abstraction techniques and then
verifies the model against the specification of the program. MAGIC has
been successfully used to check an implementation of the SSL protocol.
The SPIN [18] model checker has been used to trace errors in
data communication protocols, concurrent algorithms, and operating
systems. It uses a high level language to specify system descriptions
but also provides direct support for the use of embedded C code as
part of model specifications. However, due to the state space
explosion problem, neither SPIN nor MAGIC perform well when verifying
data-driven properties of protocols, whereas Pistachio's rules are
designed to include data modeling.
Feamster and Balakrishnan [14] define a high-level model of the BGP routing protocol by
abstracting its configuration. They use this model to build rcc, a static analysis tool that
detects faults in the router configuration.
Naumovich et al. [25] propose the FLAVERS tools,
which uses dataflow analysis techniques to verify Ada pseudocode for
communication protocols. Alur and Wang [2] formulate the
problem of verifying a protocol implementation with respect to its standardized
documentation as refinement checking.
Implementation and specification models are manually extracted from the code and
the RFC document and are compared against each other using reachability
analysis.
The method has been
successfully applied to two popular network protocols, PPP and DHCP.
Many systems have been developed for verifying properties of abstract
protocol specifications. In these systems the specification is
written in a specialized language that usually hides some
implementation details. These methods can perform powerful reasoning
about protocols, and indeed one of the assumptions behind Pistachio is
that the protocols we are checking code against are already
well-understood, perhaps using such techniques. The main difficulty of checking abstract protocols
is translating RFCs and other standards documents into the formalisms
and in picking the right level of abstraction.
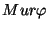 is a system for checking protocols in which abstract
rules can be extracted from actual C code [20]. The main
differences between our approach and the is a system for checking protocols in which abstract
rules can be extracted from actual C code [20]. The main
differences between our approach and the 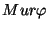 system lies in
how the rules are interpreted: in system lies in
how the rules are interpreted: in 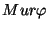 the rules are an abstraction of the
system and are derived automatically, whereas in Pistachio rules specify the actual
properties to be checked in the code. Uppaal [6] models systems (including
network protocols) as timed automata, in which transitions between
states are guarded by temporal conditions. This type of automata is
very useful in checking security protocols that use time challenges
and has been used extensively in the literature to that extent
[28,12]. In [12], Uppaal is used to model check the TLS
handshake protocol. CTL model checking can also be used to check
network protocols. In [9], an extension of the CTL semantics
is used to model AODV. the rules are an abstraction of the
system and are derived automatically, whereas in Pistachio rules specify the actual
properties to be checked in the code. Uppaal [6] models systems (including
network protocols) as timed automata, in which transitions between
states are guarded by temporal conditions. This type of automata is
very useful in checking security protocols that use time challenges
and has been used extensively in the literature to that extent
[28,12]. In [12], Uppaal is used to model check the TLS
handshake protocol. CTL model checking can also be used to check
network protocols. In [9], an extension of the CTL semantics
is used to model AODV.
Recently there has been significant research effort on
developing static analysis tools for finding bugs in software. We
list a few examples: SLAM [3] and BLAST [17] are model
checking systems that have been used to find errors in device
drivers. MOPS [8] uses model checking to check for security
property violations, such as TOCTTOU bugs and improper usage of setuid.
Metal [13] uses data flow analysis and has
been used to find many errors in operating system code.
ESP [11] uses data flow analysis and symbolic execution,
and has been used to check sequences of I/O operations in gcc.
All of
these systems have been effective in practice, but do not reason about
network protocol implementations, and it is unclear whether they can
effectively check the kinds of data-dependent rules used by Pistachio.
Dynamic analysis can also be used to trace program executions,
although we have not seen this technique used to check correctness of
implementations. Gopalakrishna et al. [16] define an
Inlined Automaton Model (IAM) that is flow- and context-sensitive and
can be derived from source code using static analysis. The model is
then used for online monitoring for intrusion detection.
Another approach to finding bugs in network protocols is
online testing. Protocol fuzzers [27] are popular tools
that look for vulnerabilities by feeding unexpected and possibly
invalid data to a protocol stack. Because fuzzers can find
hard-to-anticipate bugs, they can detect vulnerabilities that a
Pistachio user might not think to write a rule for. On the other
hand, the inherent randomness of fuzzers makes them hard to predict,
and sometimes finding even a single bug with fuzzing may take a long
time. Pistachio quickly checks for many different bugs based on a
specification, and its determinism makes it easier to integrate in the
software development process.
Our specification rules are similar to precondition/postcondition
semantics usually found in software specification systems or
design-by-contract systems like JML [19].
Similar constructs in other verification systems also include BLAST's
event specifications [17].
6 Conclusion
We have defined a rule-based method for the specification of network protocols which closely mimics protocol descriptions in RFC or similar documents. We have then shown how static analysis techniques can be employed in checking protocol implementations against the rule-based specification and provided details about our experimental prototype, Pistachio. Our experimental results show that Pistachio is very fast and is able to detect a number of security-related errors in implementations of the SSH2 and RCP protocols, while maintaining low rates of false positives and negatives.
This research was supported in part by NSF CCF-0346982 and
CCF-0430118. We thank Mike Hicks, David Wagner, Nick Petroni, R.
Sekar, and the anonymous reviewers for their helpful comments.
-
- 1
-
A. V. Aho, R. Sethi, and J. D. Ullman.
Compilers: Principles, Techniques, and Tools.
Addison Wesley, 1988.
- 2
-
R. Alur and B.-Y. Wang.
Verifying network protocol implementations by symbolic refinement
checking.
In Proceedings of International Conference on Computer-Aided
Verification, 2001.
- 3
-
T. Ball and S. K. Rajamani.
The SLAM Project: Debugging System Software via Static Analysis.
In Proceedings of POPL, 2002.
- 4
-
K. A. Bartlett, R. A. Scantlebury, and P. T. Wilkinson.
A note on reliable full-duplex transmission over half-duplex links.
Communications of the ACM, 12(5):260-261, 1969.
- 5
-
P. Baumgartner, A. Fuchs, and C. Tinelli.
Darwin: A Theorem Prover for the Model Evolution calculus.
In IJCAR Workshop on Empirically Successful First Order
Reasoning, 2004.
- 6
-
J. Bengtsson, K. G. Larsen, F. Larsson, P. Pettersson, and W. Yi.
UPPAAL - a Tool Suite for Automatic Verification of Real-Time
Systems.
In Hybrid Systems, pages 232-243, 1995.
- 7
-
S. Chaki, E. Clarke, A. Groce, S. Jha, and H. Veith.
Modular Verification of Software Components in C.
In Proceedings of the 25th International Conference on Software
Engineering, 2003.
- 8
-
H. Chen and D. Wagner.
MOPS: An Infrastructure for Examining Security Properties of
Software.
In Proceedings of the 9th ACM Conference on Computer and
Communications Security, 2002.
- 9
-
R. Corin, S. Etalle, P. H. Hartel, and A. Mader.
Timed Model Checking of Security Protocols.
In Proceedings of the 2004 ACM Workshop on Formal Methods in
Security Engineering, 2004.
- 10
-
P. Cousot and R. Cousot.
Abstract Interpretation: A Unified Lattice Model for Static Analysis
of Programs by Construction or Approximation of Fixpoints.
In Proceedings of the 4th Annual ACM SIGPLAN-SIGACT Symposium on
Principles of Programming Languages, pages 238-252, 1977.
- 11
-
M. Das, S. Lerner, and M. Seigle.
ESP: Path-Sensitive Program Verification in Polynomial Time.
In Proceedings of the 2002 ACM SIGPLAN Conference on Programming
Language Design and Implementation, pages 57-68, Berlin, Germany, June
2002.
- 12
-
G. Diaz, F. Cuartero, V. Valero, and F. Pelayo.
Automatic Verification of the TLS Handshake Protocol.
In Proceedings of the 2004 ACM Symposium on Applied Computing,
2004.
- 13
-
D. Engler, D. Y. Chen, S. Hallem, A. Chou, and B. Chelf.
Bugs as Deviant Behavior: A General Approach to Inferring Errors in
Systems Code.
In Proceedings of the 18th ACM Symposium on Operating Systems
Principles, Banff, Canada, Oct. 2001.
- 14
-
N. Feamster and H. Balakrishnan.
Detecting BGP Configuration Faults with Static Analysis.
In Proceedings of NSDI, 2005.
- 15
-
P. Godefroid.
Model Checking for Programming Languages Using Verisoft.
In Proceedings of POPL, 1997.
- 16
-
R. Gopalakrishna, E. H. Spafford, and J. Vitek.
Efficient intrusion detection using automaton inlining.
In Proceedings of the IEEE Symposium on Security and Privacy,
2005.
- 17
-
T. A. Henzinger, R. Jhala, R. Majumdar, and G. Sutre.
Software Verification with BLAST.
Lecture Notes in Computer Science, 2648:235-239, January 2003.
- 18
-
G. J. Holzmann.
The Model Checker SPIN.
Software Engineering, 23(5):279-295, 1997.
- 19
-
G. T. Leavens, K. R. M. Leino, E. Poll, C. Ruby, and B. Jacobs.
JML: notations and tools supporting detailed design in Java.
In OOPSLA 2000 Companion, 2000.
- 20
-
D. Lie, A. Chou, D. Engler, and D. L. Dill.
A Simple Method for Extracting Models for Protocol Code.
In Proceedings of the 28th Int'l Symposium on Computer
Architecture, 2001.
- 21
-
A GNU implementation of the Secure Shell protocols.
https://www.lysator.liu.se/~nisse/lsh/.
- 22
-
N. Möller.
lshd leaks fd:s to user shells, Jan. 2006.
https://lists.lysator.liu.se/pipermail/lsh-bugs/2006q1/000467.html.
- 23
-
M. Musuvathi and D. R. Engler.
Model checking large network protocol implementations.
In Proceedings of NSDI, 2004.
- 24
-
M. Musuvathi, D. Y. W. Park, A. Chou, D. R. Engler, and D. L. Dill.
CMC: A Pragmatic Approach to Model Checking Real Code.
In Proceedings of OSDI, 2002.
- 25
-
G. N. Naumovich, L. A. Clarke, and L. J. Osterweil.
Verification of Communication Protocols Using Data Flow Analysis.
In Proceedings of the 4th ACM SIGSOFT Symposium on Foundations
of Software Engineering, 1996.
- 26
-
G. C. Necula, S. McPeak, S. P. Rahul, and W. Weimer.
CIL: Intermediate Language and Tools for Analysis and
Transformation of C Programs.
In Proceedings of the 11th International Conference on Compiler
Construction, 2002.
- 27
-
P. Oehlert.
Violating assumptions with fuzzing.
IEEE Security & Privacy Magazine, 3:58-62, 2005.
- 28
-
S. Yang and J. S. Baras.
Modeling Vulnerabilities of Ad Hoc Routing Protocols.
In Proceedings of the 1st ACM workshop on Security of Ad Hoc and
Sensor Networks, 2003.
Rule-Based Static Analysis of Network Protocol Implementations
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.61)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -white -split 0 -show_section_numbers -local_icons -init_file rmc.p RMC_conference.tex
The translation was initiated by Octavian Udrea on 2006-05-10



Octavian Udrea
2006-05-10
|
