|
Security '05 Paper
[Security '05 Technical Program]
Countering Targeted File Attacks using LocationGuard
Mudhakar Srivatsa and Ling Liu
College of Computing, Georgia Institute of Technology
{mudhakar, lingliu}@cc.gatech.edu
Abstract
Serverless file systems, exemplified by CFS, Farsite and
OceanStore, have received significant attention from both the industry
and the research community. These file systems store files on a large
collection of untrusted nodes that form an overlay network. They use
cryptographic techniques to maintain file confidentiality and integrity
from malicious nodes. Unfortunately, cryptographic techniques cannot
protect a file holder from a Denial-of-Service (DoS) or a host
compromise attack. Hence, most of these distributed file systems are
vulnerable to targeted file attacks, wherein an adversary attempts to
attack a small (chosen) set of files by attacking the nodes that host
them. This paper presents LocationGuard  a
location hiding technique for securing overlay file storage systems
from targeted file attacks. LocationGuard has three essential
components: (i) location key, consisting of a random bit string (e.g.,
128 bits) that serves as the key to the location of a file, (ii)
routing guard, a secure algorithm that protects accesses to a file in
the overlay network given its location key such that neither its key
nor its location is revealed to an adversary, and (iii) a set of four
location inference guards. Our experimental results quantify the
overhead of employing LocationGuard and demonstrate its effectiveness
against DoS attacks, host compromise attacks and various location
inference attacks. a
location hiding technique for securing overlay file storage systems
from targeted file attacks. LocationGuard has three essential
components: (i) location key, consisting of a random bit string (e.g.,
128 bits) that serves as the key to the location of a file, (ii)
routing guard, a secure algorithm that protects accesses to a file in
the overlay network given its location key such that neither its key
nor its location is revealed to an adversary, and (iii) a set of four
location inference guards. Our experimental results quantify the
overhead of employing LocationGuard and demonstrate its effectiveness
against DoS attacks, host compromise attacks and various location
inference attacks.
1 Introduction
A new breed of serverless file storage services, like CFS [7], Farsite [1],
OceanStore [15] and SiRiUS [10], have recently emerged. In contrast
to traditional file systems, they harness the resources available at
desktop workstations that are distributed over a wide-area network. The
collective resources available at these desktop workstations amount to
several peta-flops of computing power and several hundred peta-bytes of
storage space [1].
These emerging trends have motivated serverless file storage as one
of the most popular application over decentralized overlay networks. An
overlay network is a virtual network formed by nodes (desktop
workstations) on top of an existing TCP/IP-network. Overlay networks
typically support a lookup protocol. A lookup operation identifies the
location of a file given its filename. Location of a file denotes the
IP-address of the node that currently hosts the file.
There are four important issues that need to be addressed to enable
wide deployment of serverless file systems for mission critical
applications.
Efficiency of the lookup protocol. There are two kinds of
lookup protocol that have been commonly deployed: the Gnutella-like
broadcast based lookup protocols [9]
and the distributed hash table (DHT) based lookup protocols [25] [19] [20]. File systems like CFS, Farsite and
OceanStore use DHT-based lookup protocols because of their ability to
locate any file in a small and bounded number of hops.
Malicious and unreliable nodes. Serverless file storage
services are faced with the challenge of having to harness the
collective resources of loosely coupled, insecure, and unreliable
machines to provide a secure, and reliable file-storage service. To
complicate matters further, some of the nodes in the overlay network
could be malicious. CFS employs cryptographic techniques to maintain
file data confidentiality and integrity. Farsite permits file write and
update operations by using a Byzantine fault-tolerant group of
meta-data servers (directory service). Both CFS and Farsite use
replication as a technique to provide higher fault-tolerance and
availability.
Targeted File Attacks. A major drawback with serverless file
systems like CFS, Farsite and Ocean-Store is that they are vulnerable
to targeted attacks on files. In a targeted attack, an adversary is
interested in compromising a small set of target files through a DoS
attack or a host compromise attack. A denial-of-service attack would
render the target file unavailable; a host compromise attack could
corrupt all the replicas of a file thereby effectively wiping out the
target file from the file system.
The fundamental problem with these systems is that: (i) the number of
replicas (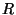 ) maintained by the system is usually much
smaller than the number of malicious nodes ( ) maintained by the system is usually much
smaller than the number of malicious nodes (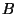 ), and (ii) the
replicas of a file are stored at publicly known locations.
Hence, malicious nodes can easily launch DoS or host compromise attacks
on the set of ), and (ii) the
replicas of a file are stored at publicly known locations.
Hence, malicious nodes can easily launch DoS or host compromise attacks
on the set of 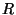 replica holders of a target file ( replica holders of a target file (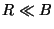 ). ).
Efficient Access Control. A read-only file system like CFS
can exercise access control by simply encrypting the contents of each
file, and distributing the keys only to the legal users of that file.
Farsite, a read-write file system, exercises access control using
access control lists (ACL) that are maintained using a
Byzantine-fault-tolerant protocol. However, access control is not truly
distributed in Farsite because all users are authenticated by a small
collection of directory-group servers. Further, PKI (public-key
Infrastructure) based authentication and Byzantine fault tolerance
based authorization are known to be more expensive than a simple and
fast capability-based access control mechanism [6].
In this paper we present LocationGuard as an effective
technique for countering targeted file attacks. The fundamental idea
behind LocationGuard is to hide the very location of a file and
its replicas such that, a legal user who possesses a file's location
key can easily and securely locate the file on the overlay network;
but without knowing the file's location key, an adversary would not be
able to even locate the file, let alone access it or attempt to attack
it. Further, an adversary would not be even able to learn if a
particular file exists in the file system or not. LocationGuard
comprises of three essential components. The first component of
LocationGuard is a location key, which is a 128-bit string used as a
key to the location of a file in the overlay network. A file's location
key is used to generate legal capabilities (tokens) that can be used to
access its replicas. The second component is the routing guard, a
secure algorithm to locate a file in the overlay network given its
location key such that neither the key nor the location is revealed to
an adversary. The third component is an extensible collection of
location inference guards, which protect the system from traffic
analysis based inference attacks, such as lookup frequency inference
attacks, end-user IP-address inference attacks, file replica inference
attacks, and file size inference attacks. LocationGuard presents a
careful combination of location key, routing guard, and location
inference guards, aiming at making it very hard for an adversary to
infer the location of a target file by either actively or passively
observing the overlay network.
In addition traditional cryptographic guarantees like file
confidentiality and integrity, LocationGuard mitigates
denial-of-service (DoS) and host compromise attacks, while adding very
little performance overhead and very minimal storage overhead to the
file system. Our initial experiments quantify the overhead of employing
LocationGuard and demonstrate its effectiveness against DoS attacks,
host compromise attacks and various location inference attacks.
The rest of the paper is organized as follows. Section 2 provides terminology and background on
overlay network and serverless file systems like CFS and Farsite.
Section 3 describes our threat
model in detail. We present an abstract functional description of
LocationGuard in Section 4. Section 4, 5
describes the design of our location keys and Section 6 presents a detailed
description of the routing guard. We outline a brief discussion on
overall system management in Section 8
and present a thorough experimental evaluation of LocationGuard in
Section 9. Finally, we present some
related work in Section 10, and
conclude the paper in Section 11.
2 Background and Terminology
In this section, we give a brief overview on the vital properties of
DHT-based overlay networks and their lookup protocols (e.g., Chord [25], CAN [19],
Pastry [20], Tapestry [3]). All these lookup protocols are
fundamentally based on distributed hash tables, but differ in
algorithmic and implementation details. All of them store the mapping
between a particular search key and its associated  (file) in a distributed manner across the network,
rather than storing them at a single location like a conventional hash
table. Given a search key, these techniques locate its
associated (file) in a distributed manner across the network,
rather than storing them at a single location like a conventional hash
table. Given a search key, these techniques locate its
associated  (file) in a small and bounded number of
hops within the overlay network. This is realized using three main
steps. First, nodes and search keys are hashed to a common identifier
space such that each node is given a unique identifier and is made
responsible for a certain set of search keys. Second, the mapping of
search keys to nodes uses policies like numerical closeness or
contiguous regions between two node identifiers to determine the
(non-overlapping) region (segment) that each node will be responsible
for. Third, a small and bounded lookup cost is guaranteed by
maintaining a tiny routing table and a neighbor list at each node. (file) in a small and bounded number of
hops within the overlay network. This is realized using three main
steps. First, nodes and search keys are hashed to a common identifier
space such that each node is given a unique identifier and is made
responsible for a certain set of search keys. Second, the mapping of
search keys to nodes uses policies like numerical closeness or
contiguous regions between two node identifiers to determine the
(non-overlapping) region (segment) that each node will be responsible
for. Third, a small and bounded lookup cost is guaranteed by
maintaining a tiny routing table and a neighbor list at each node.
In the context of a file system, the search key can be a filename
and the identifier can be the IP address of a node. All the available
node's IP addresses are hashed using a hash function and each of them
store a small routing table (for example, Chord's routing table has
only 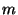 entries for an entries for an 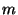 -bit hash
function and typically -bit hash
function and typically 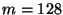 ) to locate other nodes.
Now, to locate a particular file, its filename is hashed using the same
hash function and the node responsible for that file is obtained using
the concrete mapping policy. This operation of locating the appropriate
node is called a lookup. ) to locate other nodes.
Now, to locate a particular file, its filename is hashed using the same
hash function and the node responsible for that file is obtained using
the concrete mapping policy. This operation of locating the appropriate
node is called a lookup.
Serverless file system like CFS, Farsite and Ocean-Store are layered
on top of DHT-based protocols. These file systems typically provide the
following properties: (1) A file lookup is guaranteed to succeed if and
only if the file is present in the system, (2) File lookup terminates
in a small and bounded number of hops, (3) The files are uniformly
distributed among all active nodes, and (4) The system handles dynamic
node joins and leaves.
In the rest of this paper, we assume that Chord [25] is used as the overlay network's
lookup protocol. However, the results presented in this paper are
applicable for most DHT-based lookup protocols.
3 Threat Model
Adversary refers to a logical entity that controls and coordinates all
actions by malicious nodes in the system. A node is said to be
malicious if the node either intentionally or unintentionally fails to
follow the system's protocols correctly. For example, a malicious node
may corrupt the files assigned to them and incorrectly (maliciously)
implement file read/write operations. This definition of adversary
permits collusions among malicious nodes.
We assume that the underlying IP-network layer may be insecure.
However, we assume that the underlying IP-network infrastructure such
as domain name service (DNS), and the network routers cannot be
subverted by the adversary.
An adversary is capable of performing two types of attacks on the
file system, namely, the denial-of-service attack, and the host
compromise attack. When a node is under denial-of-service attack, the
files stored at that node are unavailable. When a node is compromised,
the files stored at that node could be either unavailable or corrupted.
We model the malicious nodes as having a large but bounded amount of
physical resources at their disposal. More specifically, we assume that
a malicious node may be able to perform a denial-of-service attack only
on a finite and bounded number of good nodes, denoted by 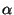 . We limit the rate at which malicious nodes may
compromise good nodes and use . We limit the rate at which malicious nodes may
compromise good nodes and use 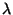 to denote
the mean rate per malicious node at which a good node can be
compromised. For instance, when there are to denote
the mean rate per malicious node at which a good node can be
compromised. For instance, when there are 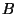 malicious nodes
in the system, the net rate at which good nodes are compromised is malicious nodes
in the system, the net rate at which good nodes are compromised is 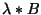 (node compromises per unit time). Note
that it does not really help for one adversary to pose as multiple
nodes (say using a virtualization technology) since the effective
compromise rate depends only on the aggregate strength of the
adversary. Every compromised node behaves maliciously. For instance, a
compromised node may attempt to compromise other good nodes. Every good
node that is compromised would independently recover at rate (node compromises per unit time). Note
that it does not really help for one adversary to pose as multiple
nodes (say using a virtualization technology) since the effective
compromise rate depends only on the aggregate strength of the
adversary. Every compromised node behaves maliciously. For instance, a
compromised node may attempt to compromise other good nodes. Every good
node that is compromised would independently recover at rate 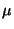 . Note that the recovery of a compromised node is
analogous to cleaning up a virus or a worm from an infected node. When
the recovery process ends, the node stops behaving maliciously. Unless
and otherwise specified we assume that the rates . Note that the recovery of a compromised node is
analogous to cleaning up a virus or a worm from an infected node. When
the recovery process ends, the node stops behaving maliciously. Unless
and otherwise specified we assume that the rates 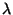 and
and 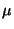 follow an exponential distribution. follow an exponential distribution.
3.1 Targeted File Attacks
Targeted file attack refers to an attack wherein an adversary attempts
to attack a small (chosen) set of files in the system. An attack on a
file is successful if the target file is either rendered unavailable or
corrupted. Let 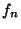 denote the name of a file denote the name of a file  and and 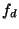 denote the data in file denote the data in file  .
Given .
Given 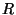 replicas of a file replicas of a file  ,
file ,
file  is unavailable (or corrupted) if at least
a threshold is unavailable (or corrupted) if at least
a threshold 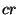 number of its replicas are unavailable
(or corrupted). For example, for read/write files maintained by a
Byzantine quorum [1], number of its replicas are unavailable
(or corrupted). For example, for read/write files maintained by a
Byzantine quorum [1], 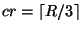 . For encrypted and authenticated
files, . For encrypted and authenticated
files, 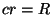 , since the file can be successfully
recovered as long as at least one of its replicas is available (and
uncorrupt) [7]. Most P2P trust management
systems such as [27] uses a simple
majority vote on the replicas to compute the actual trust values of
peers, thus we have , since the file can be successfully
recovered as long as at least one of its replicas is available (and
uncorrupt) [7]. Most P2P trust management
systems such as [27] uses a simple
majority vote on the replicas to compute the actual trust values of
peers, thus we have 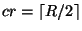 . .
Distributed file systems like CFS and Farsite are highly vulnerable
to target file attacks since the target file can be rendered
unavailable (or corrupted) by attacking a very small set of
nodes in the system. The key problem arises from the fact that these
systems store the replicas of a file  at publicly
known locations [13] for easy lookup.
For instance, CFS stores a file at publicly
known locations [13] for easy lookup.
For instance, CFS stores a file  at locations
derivable from the public-key of its owner. An adversary can attack any
set of at locations
derivable from the public-key of its owner. An adversary can attack any
set of 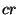 replica holders of file replica holders of file  , to
render file , to
render file  unavailable (or corrupted). Farsite
utilizes a small collection of publicly known nodes for implementing a
Byzantine fault-tolerant directory service. On compromising the
directory service, an adversary could obtain the locations of all the
replicas of a target file. unavailable (or corrupted). Farsite
utilizes a small collection of publicly known nodes for implementing a
Byzantine fault-tolerant directory service. On compromising the
directory service, an adversary could obtain the locations of all the
replicas of a target file.
Files on an overlay network have two primary attributes: (i) content
and (ii) location. File content could be protected from an
adversary using cryptographic techniques. However, if the location of a
file on the overlay network is publicly known, then the file holder is
susceptible to DoS and host compromise attacks. LocationGuard provides
mechanisms to hide files in an overlay network such that only a legal
user who possesses a file's location key can easily locate it. Further,
an adversary would not even be able to learn whether a particular file
exists in the file system or not. Thus, any previously known attacks on
file contents would not be applicable unless the adversary succeeds in
locating the file. It is important to note that LocationGuard is
oblivious to whether or not file contents are encrypted. Hence,
LocationGuard can be used to protect files whose contents cannot be
encrypted, say, to permit regular expression based keyword search on
file contents.
4 LocationGuard
Figure 1:
LocationGuard: System Architecture
![\includegraphics[width=\linewidth]{fig/system.eps}](img23.png)
|
Figure 2:
LocationGuard: Conceptual Design
![\includegraphics[width=\linewidth]{fig/lg.eps}](img24.png)
|
4.1 Overview
We first present a high level overview of LocationGuard. Figure 1 shows an architectural overview of
a file system powered by LocationGuard. LocationGuard operates on top
of an overlay network of 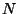 nodes. Figure 2 provides a sketch of the conceptual
design of LocationGuard. LocationGuard scheme guards the location of
each file and its access with two objectives: (1) to hide the actual
location of a file and its replicas such that only legal users who hold
the file's location key can easily locate the file on the overlay
network, and (2) to guard lookups on the overlay network from being
eavesdropped by an adversary. LocationGuard consists of three core
components. The first component is location key, which controls
the transformation of a filename into its location on the overlay
network, analogous to a traditional cryptographic key that
controls the transformation of plaintext into ciphertext. The second
component is the routing guard, which makes the location of a
file unintelligible. The routing guard is, to some extent, analogous to
a traditional cryptographic algorithm which makes a file's
contents unintelligible. The third component of LocationGuard includes
an extensible package of location inference guards that protect the
file system from indirect attacks. Indirect attacks are those attacks
that exploit a file's metadata information such as file access
frequency, end-user IP-address, equivalence of file replica contents
and file size to infer the location of a target file on the overlay
network. In this paper we focus only on the first two components,
namely, the location key and the routing guard. For a detailed
discussion on location inference guards refer to our tech-report [23]. nodes. Figure 2 provides a sketch of the conceptual
design of LocationGuard. LocationGuard scheme guards the location of
each file and its access with two objectives: (1) to hide the actual
location of a file and its replicas such that only legal users who hold
the file's location key can easily locate the file on the overlay
network, and (2) to guard lookups on the overlay network from being
eavesdropped by an adversary. LocationGuard consists of three core
components. The first component is location key, which controls
the transformation of a filename into its location on the overlay
network, analogous to a traditional cryptographic key that
controls the transformation of plaintext into ciphertext. The second
component is the routing guard, which makes the location of a
file unintelligible. The routing guard is, to some extent, analogous to
a traditional cryptographic algorithm which makes a file's
contents unintelligible. The third component of LocationGuard includes
an extensible package of location inference guards that protect the
file system from indirect attacks. Indirect attacks are those attacks
that exploit a file's metadata information such as file access
frequency, end-user IP-address, equivalence of file replica contents
and file size to infer the location of a target file on the overlay
network. In this paper we focus only on the first two components,
namely, the location key and the routing guard. For a detailed
discussion on location inference guards refer to our tech-report [23].
In the following subsections, we first present the main concepts
behind location keys and location hiding (Section 4.2) and describe a reference model for
serverless file systems that operate on LocationGuard (Section 4.3). Then we present the
concrete design of LocationGuard's core components: the location key
(Section 5), and the routing
guard (Section 6).
4.2 Concepts and Definitions
In this section we define the concept of location keys and its location
hiding properties. We discuss the concrete design of location key
implementation and how location keys and location guards protect a file
system from targeted file attacks in the subsequent sections.
Consider an overlay network of size 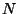 with a
Chord-like lookup protocol with a
Chord-like lookup protocol 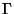 . Let . Let 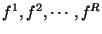 denote the denote the 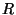 replicas of a
file replicas of a
file  . Location of a replica . Location of a replica 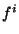 refers to the IP-address of the node (replica holder) that stores
replica
refers to the IP-address of the node (replica holder) that stores
replica 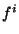 . A file lookup algorithm is defined as a
function that accepts . A file lookup algorithm is defined as a
function that accepts 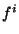 and outputs its location on
the overlay network. Formally we have and outputs its location on
the overlay network. Formally we have 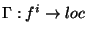 maps a replica maps a replica 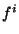 to
its location to
its location 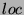 on the overlay network on the overlay network 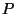 . .
Definition
1 Location Key: A location key 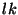 of
a file of
a file  is a relatively small amount ( is a relatively small amount (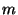 -bit binary string, typically -bit binary string, typically 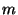 = 128) of
information that is used by a Lookup algorithm = 128) of
information that is used by a Lookup algorithm 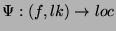 to customize the transformation
of a file into its location such that the following three properties
are satisfied: to customize the transformation
of a file into its location such that the following three properties
are satisfied:
- Given the location key of a file
 , it is easy
to locate the , it is easy
to locate the 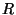 replicas of file replicas of file  . .
- Without knowing the location key of a file
 , it
is hard for an adversary to locate any of its replicas. , it
is hard for an adversary to locate any of its replicas.
- The location key
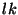 of a file of a file  should not be exposed to an adversary when it is used to access the
file
should not be exposed to an adversary when it is used to access the
file  . .
Informally, location keys are keys with location hiding property.
Each file in the system is associated with a location key that is kept
secret by the users of that file. A location key for a file  determines the locations of its replicas in the overlay
network. Note that the lookup algorithm determines the locations of its replicas in the overlay
network. Note that the lookup algorithm 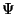 is publicly
known; only a file's location key is kept secret. is publicly
known; only a file's location key is kept secret.
Property 1 ensures that valid users of a file  can
easily access it provided they know its location key can
easily access it provided they know its location key  .
Property 2 guarantees that illegal users who do not have the correct
location key will not be able to locate the file on the overlay
network, making it harder for an adversary to launch a targeted file
attack. Property 3 warrants that no information about the location key .
Property 2 guarantees that illegal users who do not have the correct
location key will not be able to locate the file on the overlay
network, making it harder for an adversary to launch a targeted file
attack. Property 3 warrants that no information about the location key  of a file of a file  is revealed to an adversary
when executing the lookup algorithm is revealed to an adversary
when executing the lookup algorithm  . .
Having defined the concept of location key, we present a reference
model for a file system that operates on LocationGuard. We use this
reference model to present a concrete design of LocationGuard's three
core components: the location key, the routing guard and the location
inference guards.
4.3 Reference Model
A serverless file system may implement read/write operations by
exercising access control in a number of ways. For example,
Farsite [1] uses an access
control list maintained among a small number of directory servers
through a Byzantine fault tolerant protocol. CFS [7], a read-only file system, implements
access control by encrypting the files and distributing the file
encryption keys only to the legal users of a file. In this section we
show how a LocationGuard based file system exercises access control.
In contrast to other serverless file systems, a LocationGuard based
file system does not directly authenticate any user attempting to
access a file. Instead, it uses location keys to implement a
capability-based access control mechanism, that is, any user who
presents the correct file capability (token) is permitted access to
that file. In addition to file token based access control,
LocationGuard derives the encryption key for a file from its location
key. This makes it very hard for an adversary to read file data from
compromised nodes. Furthermore, it utilizes routing guard and location
inference guards to secure the locations of files being accessed on the
overlay network. Our access control policy is simple: if you can
name a file, then you can access it. However, we do not use a file
name directly; instead, we use a pseudo-filename (128-bit binary
string) generated from a file's name and its location key (see Section 5 for detail). The responsibility
of access control is divided among the file owner, the legal file
users, and the file replica holders and is managed in a decentralized
manner.
File Owner. Given a file  , its owner , its owner  is responsible for securely distributing is responsible for securely distributing  's
location key 's
location key 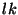 (only) to those users who are authorized
to access the file (only) to those users who are authorized
to access the file  . .
Legal User. A user 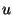 who has obtained the valid
location key of file who has obtained the valid
location key of file  is called a legal user of is called a legal user of  . Legal users are authorized to access any replica of file . Legal users are authorized to access any replica of file  . Given a file . Given a file  's location key 's location key 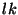 , a
legal user , a
legal user 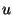 can generate the replica location token can generate the replica location token  for its for its 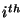 replica. Note that we use replica. Note that we use  as both the pseudo-filename and the capability of as both the pseudo-filename and the capability of 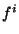 . The user . The user 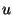 now uses the lookup algorithm now uses the lookup algorithm 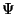 to obtain the IP-address of node to obtain the IP-address of node  = = 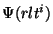 (pseudo-filename (pseudo-filename  ). User ). User 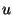 gains access to replica gains access to replica 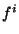 by presenting
the token by presenting
the token  to node to node  (capability (capability  ). ).
Non-malicious Replica Holder.
Assume that a node  is responsible for storing
replica is responsible for storing
replica 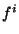 . Internally, node . Internally, node  stores this file content under a file name
stores this file content under a file name  . Note that
node . Note that
node  does not need to know the actual file name
( does not need to know the actual file name
( ) of a locally stored file ) of a locally stored file  . Also, by
design, given the internal file name . Also, by
design, given the internal file name  , node , node  cannot guess its actual file name (see Section 5). When a node cannot guess its actual file name (see Section 5). When a node  receives a read/write request on a file
receives a read/write request on a file  it checks if
a file named it checks if
a file named  is present locally. If so, it directly
performs the requested operation on the local file is present locally. If so, it directly
performs the requested operation on the local file  .
Access control follows from the fact that it is very hard for an
adversary to guess correct file tokens. .
Access control follows from the fact that it is very hard for an
adversary to guess correct file tokens.
Malicious Replica Holder. Let us consider the case where the
node  that stores a replica that stores a replica 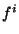 is
malicious. Note that node is
malicious. Note that node  's response to a file read/write
request can be undefined. Note that we have assumed that the replicas
stored at malicious nodes are always under attack (recall that up to 's response to a file read/write
request can be undefined. Note that we have assumed that the replicas
stored at malicious nodes are always under attack (recall that up to 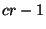 out of out of 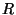 file replicas could be
unavailable or corrupted). Hence, the fact that a malicious replica
holder incorrectly implements file read/write operation or that the
adversary is aware of the tokens of those file replicas stored at
malicious nodes does not harm the system. Also, by design, an adversary
who knows one token file replicas could be
unavailable or corrupted). Hence, the fact that a malicious replica
holder incorrectly implements file read/write operation or that the
adversary is aware of the tokens of those file replicas stored at
malicious nodes does not harm the system. Also, by design, an adversary
who knows one token  for replica for replica 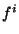 would not be able to guess the file name
would not be able to guess the file name  or its location
key or its location
key 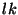 or the tokens for others replicas of file or the tokens for others replicas of file
 (see Section 5). (see Section 5).
Adversary. An adversary cannot access any replica of file  stored at a good node simply because it cannot guess the
token stored at a good node simply because it cannot guess the
token  without knowing its location key.
However, when a good node is compromised an adversary would be able to
directly obtain the tokens for all files stored at that node. In
general, an adversary could compile a list of tokens as it compromises
good nodes, and corrupt the file replicas corresponding to these tokens
at any later point in time. Eventually, the adversary would succeed in
corrupting without knowing its location key.
However, when a good node is compromised an adversary would be able to
directly obtain the tokens for all files stored at that node. In
general, an adversary could compile a list of tokens as it compromises
good nodes, and corrupt the file replicas corresponding to these tokens
at any later point in time. Eventually, the adversary would succeed in
corrupting 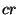 or more replicas of a file or more replicas of a file  without knowing its location key. LocationGuard addresses
such attacks using location rekeying technique discussed in Section 7.3. without knowing its location key. LocationGuard addresses
such attacks using location rekeying technique discussed in Section 7.3.
In the subsequent sections, we show how to generate a replica
location token  ( (
 ) from a file ) from a file  and its location
key (Section 5), and how the
lookup algorithm and its location
key (Section 5), and how the
lookup algorithm  performs a lookup on a pseudo-filename performs a lookup on a pseudo-filename  without revealing the capability without revealing the capability  to malicious nodes in the overlay network (Section 6). It is important to note that
the ability of guarding the lookup from attacks like eavesdropping is
critical to the ultimate goal of file location hiding scheme, since a
lookup operation using a lookup protocol (such as Chord) on identifier
to malicious nodes in the overlay network (Section 6). It is important to note that
the ability of guarding the lookup from attacks like eavesdropping is
critical to the ultimate goal of file location hiding scheme, since a
lookup operation using a lookup protocol (such as Chord) on identifier  typically proceeds in plain-text through a sequence of
nodes on the overlay network. Hence, an adversary may collect file
tokens by simply sniffing lookup queries over the overlay network. The
adversary could use these stolen file tokens to perform write
operations on the corresponding file replicas, and thus corrupt them,
without the knowledge of their location keys. typically proceeds in plain-text through a sequence of
nodes on the overlay network. Hence, an adversary may collect file
tokens by simply sniffing lookup queries over the overlay network. The
adversary could use these stolen file tokens to perform write
operations on the corresponding file replicas, and thus corrupt them,
without the knowledge of their location keys.
5 Location Keys
The first and most simplistic component of LocationGuard is the concept
of location keys. The design of location key needs to address the
following two questions: (1) How to choose a location key? (2) How to
use a location key to generate a replica location token  the
capability to access a file replica? the
capability to access a file replica?
The first step in designing location keys is to determining the
type of string used as the identifier of a location key. Let user 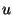 be the owner of a file be the owner of a file  . User . User 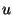 should choose a long random bit string (128-bits) should choose a long random bit string (128-bits) 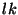 as the location key for file as the location key for file  . The location
key . The location
key 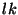 should be hard to guess. For example, the
key should be hard to guess. For example, the
key 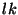 should not be semantically attached to or
derived from the file name ( should not be semantically attached to or
derived from the file name ( ) or the owner name ( ) or the owner name (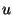 ). ).
The second step is to find a pseudo-random function to
derive the replica location tokens  ( (
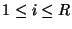 ) from the filename ) from the filename  and
its location key and
its location key 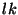 . The pseudo-filename . The pseudo-filename  is used as a file replica identifier to locate the
is used as a file replica identifier to locate the 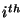 replica of file
replica of file  on the overlay network. Let on the overlay network. Let 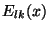 denote a keyed pseudo-random function with input denote a keyed pseudo-random function with input 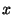 and a secret key and a secret key 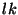 and and  denotes string concatenation. We derive the
location token denotes string concatenation. We derive the
location token  = = 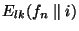 (recall that (recall that  denotes the name of file
denotes the name of file  ). Given a replica's identifier ). Given a replica's identifier  , one can use the lookup protocol , one can use the lookup protocol  to locate it on the overlay network. The function
to locate it on the overlay network. The function 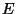 should satisfy the following conditions:
should satisfy the following conditions:
[1a] Given 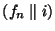 and and  it is easy to
compute it is easy to
compute 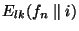 . .
[2a] Given 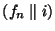 it is hard to guess
it is hard to guess 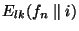 without
knowing without
knowing  . .
[2b] Given 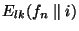 it is hard to guess the file name it is hard to guess the file name 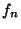 . .
[2c] Given 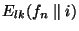 and the file name and the file name 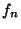 it
is hard to guess it
is hard to guess 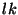 . .
Condition 1a ensures that it is very easy for a valid user to locate a
file  as long as it is aware of the file's
location key as long as it is aware of the file's
location key 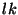 . Condition 2a, states that it should be
very hard for an adversary to guess the location of a target file . Condition 2a, states that it should be
very hard for an adversary to guess the location of a target file  without knowing its location key. Condition 2b ensures
that even if an adversary obtains the identifier without knowing its location key. Condition 2b ensures
that even if an adversary obtains the identifier  of replica
of replica 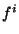 , he/she cannot deduce the file name , he/she cannot deduce the file name  . Finally, Condition 2c requires that even if an adversary
obtains the identifiers of one or more replicas of file . Finally, Condition 2c requires that even if an adversary
obtains the identifiers of one or more replicas of file  ,
he/she would not be able to derive the location key ,
he/she would not be able to derive the location key 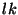 from them. Hence, the adversary still has no clue about the remaining
replicas of the file
from them. Hence, the adversary still has no clue about the remaining
replicas of the file  (by Condition 2a). Conditions
2b and 2c play an important role in ensuring good location hiding
property. This is because for any given file (by Condition 2a). Conditions
2b and 2c play an important role in ensuring good location hiding
property. This is because for any given file  ,
some of the replicas of file ,
some of the replicas of file  could be stored at malicious
nodes. Thus an adversary could be aware of some of the replica
identifiers. Finally, observe that Condition 1a and Conditions {2a, 2b,
2c} map to Property 1 and Property 2 in Definition 1 (in Section 4.2) respectively. could be stored at malicious
nodes. Thus an adversary could be aware of some of the replica
identifiers. Finally, observe that Condition 1a and Conditions {2a, 2b,
2c} map to Property 1 and Property 2 in Definition 1 (in Section 4.2) respectively.
There are a number of cryptographic tools that satisfies our
requirements specified in Conditions 1a), 2a), 2b) and 2c). Some
possible candidates for the function 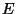 are (i) a
keyed-hash function like HMAC-MD5 [14],
(ii) a symmetric key encryption algorithm like DES [8] or AES [16],
and (iii) a PKI based encryption algorithm like RSA [21]. We chose to use a keyed-hash function
like HMAC-MD5 because it can be computed very efficiently. HMAC-MD5
computation is about 40 times faster than AES encryption and about 1000
times faster than RSA encryption using the standard OpenSSL library [17]. In the remaining part of this
paper, we use are (i) a
keyed-hash function like HMAC-MD5 [14],
(ii) a symmetric key encryption algorithm like DES [8] or AES [16],
and (iii) a PKI based encryption algorithm like RSA [21]. We chose to use a keyed-hash function
like HMAC-MD5 because it can be computed very efficiently. HMAC-MD5
computation is about 40 times faster than AES encryption and about 1000
times faster than RSA encryption using the standard OpenSSL library [17]. In the remaining part of this
paper, we use 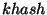 to denote a keyed-hash function that
is used to derive a file's replica location tokens from its name and
its secret location key. to denote a keyed-hash function that
is used to derive a file's replica location tokens from its name and
its secret location key.
6 Routing guard
The second and fundamental component of LocationGuard is the routing
guard. The design of routing guard aims at securing the lookup of file  such that it will be very hard for an adversary to obtain
the replica location tokens by eavesdropping on the overlay network.
Concretely, let such that it will be very hard for an adversary to obtain
the replica location tokens by eavesdropping on the overlay network.
Concretely, let  ( (
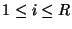 ) denote a replica location token derived
from the file name ) denote a replica location token derived
from the file name  , the replica number , the replica number 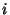 , and , and  `s location key identifier `s location key identifier 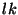 . We
need to secure the lookup algorithm . We
need to secure the lookup algorithm 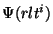 such that the lookup on pseudo-filename such that the lookup on pseudo-filename  does not reveal the capability does not reveal the capability  to other nodes on the overlay network. Note that a file's capability
to other nodes on the overlay network. Note that a file's capability  does not reveal the file's name; but it allows an
adversary to write on the file and thus corrupt it (see reference file
system in Section 4.3). does not reveal the file's name; but it allows an
adversary to write on the file and thus corrupt it (see reference file
system in Section 4.3).
There are two possible approaches to implement a secure lookup
algorithm: (1) centralized approach and (2) decentralized approach. In
the centralized approach, one could use a trusted location server [12] to return the location of any
file on the overlay network. However, such a location server would
become a viable target for DoS and host compromise attacks.
In this section, we present a decentralized secure lookup protocol
that is built on top of the Chord protocol. Note that a naive
Chord-like lookup protocol 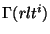 cannot be directly used because it reveals the
token cannot be directly used because it reveals the
token  to other nodes on the overlay network. to other nodes on the overlay network.
The fundamental idea behind the routing guard is as follows. Given a
file  's location key 's location key 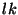 and replica
number and replica
number 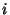 , we want to find a safe region in the
identifier space where we can obtain a huge collection of obfuscated
tokens, denoted by , we want to find a safe region in the
identifier space where we can obtain a huge collection of obfuscated
tokens, denoted by 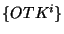 , such that, with high
probability, , such that, with high
probability, 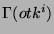 = = 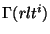 , , 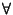 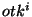 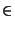 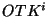 . We call . We call 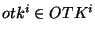 an obfuscated identifier of the token an obfuscated identifier of the token  . Each time a user . Each time a user 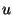 wishes to lookup
a token wishes to lookup
a token  , it performs a lookup on some randomly
chosen token , it performs a lookup on some randomly
chosen token 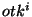 from the obfuscated identifier set from the obfuscated identifier set 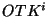 . Routing guard ensures that even if an adversary were
to observe obfuscated identifier from the set . Routing guard ensures that even if an adversary were
to observe obfuscated identifier from the set 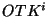 for one full year, it would be highly infeasible for the adversary to
guess the token
for one full year, it would be highly infeasible for the adversary to
guess the token  . .
We now describe the concrete implementation of the routing guard.
For the sake of simplicity, we assume a unit circle for the Chord's
identifier space; that is, node identifiers and file identifiers are
real values from 0 to 1 that are arranged on the Chord ring in the
anti-clockwise direction. Let 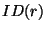 denote the
identifier of node denote the
identifier of node  . If . If  is the
destination node of a lookup on file identifier is the
destination node of a lookup on file identifier  ,
i.e., ,
i.e., 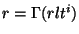 ,
then ,
then  is the node that immediately succeeds is the node that immediately succeeds  in the anti-clockwise direction on the Chord ring.
Formally, in the anti-clockwise direction on the Chord ring.
Formally, 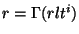 if if 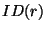 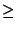  and there exists no other nodes, say and there exists no other nodes, say 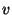 , on the Chord ring such that , on the Chord ring such that 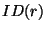  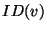 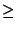  . .
Figure 3:
Lookup Using File Identifier Obfuscation: Illustration
![\includegraphics[width=\linewidth]{fig/perturb.eps}](img64.png)
|
Table 1:
Lookup Identifier obfuscation
|
We first introduce the concept of safe obfuscation to guide us
in finding an obfuscated identifier set 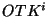 for a given
replica location token for a given
replica location token  . We say that an obfuscated
identifier . We say that an obfuscated
identifier 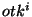 is a safe obfuscation of identifier is a safe obfuscation of identifier  if and only if a lookup on both if and only if a lookup on both  and
and 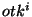 result in the same physical node result in the same physical node  . For example, in Figure 3,
identifier . For example, in Figure 3,
identifier 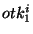 is a safe obfuscation of identifier is a safe obfuscation of identifier  ( (
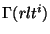 = = 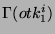 = =  ), while identifier ), while identifier 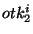 is unsafe ( is unsafe (
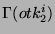 = = 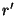 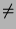  ). ).
We define the set 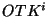 as a set of all identifiers
in the range ( as a set of all identifiers
in the range (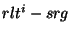 , ,  ), where ), where 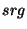 denotes a safe obfuscation range ( denotes a safe obfuscation range (
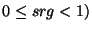 . When a user intends to query for a replica
location token . When a user intends to query for a replica
location token  , the user actually performs a lookup
on an obfuscated identifier , the user actually performs a lookup
on an obfuscated identifier 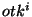 = = 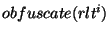 = =  
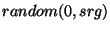 . The function . The function 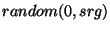 returns a number chosen uniformly and
randomly in the range returns a number chosen uniformly and
randomly in the range 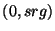 . .
We choose a safe value 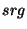 such that: such that:
(C1) With high
probability, any obfuscated identifier is a safe obfuscation of the
token  . .
(C2) Given a set of
obfuscated identifiers { } it is very hard for an adversary to guess the actual
identifier } it is very hard for an adversary to guess the actual
identifier  . .
Note that if 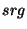 is too small condition C1 is more likely
to hold, while condition C2 is more likely to fail. In contrast, if is too small condition C1 is more likely
to hold, while condition C2 is more likely to fail. In contrast, if 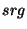 is too big, condition C2 is more likely to hold but
condition C1 is more likely to fail. In our first prototype development
of LocationGuard, we introduce a system defined parameter is too big, condition C2 is more likely to hold but
condition C1 is more likely to fail. In our first prototype development
of LocationGuard, we introduce a system defined parameter 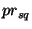 to denote the minimum probability that any
obfuscation is required to be safe. In the subsequent sections, we
present a technique to derive to denote the minimum probability that any
obfuscation is required to be safe. In the subsequent sections, we
present a technique to derive 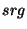 as a function
of as a function
of 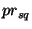 . This permits us to quantify the
tradeoff between condition C1 and condition C2.
Observe from Figure 3 that a
obfuscation . This permits us to quantify the
tradeoff between condition C1 and condition C2.
Observe from Figure 3 that a
obfuscation 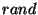 on identifier on identifier  is safe if
is safe if   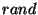  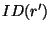 ,
where ,
where 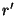 is the immediate predecessor of
node is the immediate predecessor of
node  on the Chord ring. Thus, we have on the Chord ring. Thus, we have 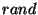   
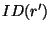 . The expression . The expression  
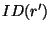 denotes the distance between identifiers denotes the distance between identifiers  and and 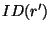 on the Chord identifier ring, denoted by on the Chord identifier ring, denoted by 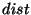 ( ( , , 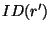 ). Hence, we say that a obfuscation ). Hence, we say that a obfuscation 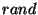 is safe with respect to identifier is safe with respect to identifier  if and only if
if and only if 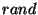  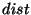 ( ( , , 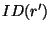 ), or equivalently, ), or equivalently, 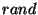 is chosen
from the range (0, is chosen
from the range (0, 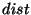 ( ( , , 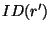 )). )).
We use Theorem 6.1 to show
that Pr(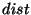 ( ( , , 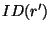 ) ) 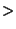 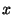 ) = ) = 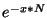 , where , where 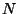 denotes the number of nodes on
the overlay network and denotes the number of nodes on
the overlay network and 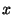 denotes any value satisfying denotes any value satisfying 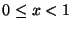 . Informally, the theorem states that the
probability that the predecessor node . Informally, the theorem states that the
probability that the predecessor node 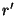 is
further away from the identifier is
further away from the identifier  decreases
exponentially with the distance. For a detailed proof please refer to
our tech-report [23]. decreases
exponentially with the distance. For a detailed proof please refer to
our tech-report [23].
Observe that an obfuscation 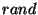 is safe with
respect to is safe with
respect to  if if 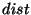 ( ( , , 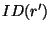 ) )  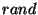 , the
probability that a obfuscation , the
probability that a obfuscation 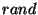 is safe can
be calculated using is safe can
be calculated using 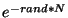 . .
Now, one can ensure that the minimum probability of any obfuscation
being safe is 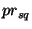 as follows. We first use as follows. We first use 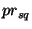 to obtain an upper bound on to obtain an upper bound on  :
By :
By   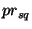 , we have, , we have, 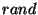  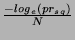 . Hence, if . Hence, if 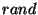 is chosen from a safe range
is chosen from a safe range 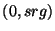 , where , where 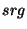 = = 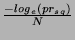 , then all obfuscations are
guaranteed to be safe with a probability greater than or equal to , then all obfuscations are
guaranteed to be safe with a probability greater than or equal to 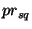 . .
For instance, when we set 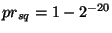 and and 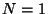 million
nodes, million
nodes, 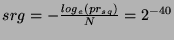 . Hence, on a
128-bit Chord ring . Hence, on a
128-bit Chord ring 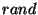 could be chosen from a range
of size could be chosen from a range
of size 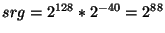 . Table 1 shows the size of a . Table 1 shows the size of a 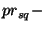 safe obfuscation range safe obfuscation range 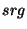 for different
values of for different
values of 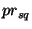 . Observe that if we set . Observe that if we set 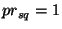 , then , then 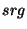 = = 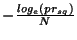 = 0. Hence, if we want 100%
safety, the obfuscation range = 0. Hence, if we want 100%
safety, the obfuscation range 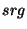 must be zero,
i.e., the token must be zero,
i.e., the token  cannot be obfuscated. cannot be obfuscated.
Theorem 6.1 Let 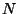 denote the total number of nodes in the system. Let 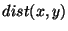 denote the distance between two identifiers 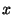 and 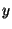 on a Chord's unit circle.
Let node 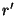 be the node that is the immediate
predecessor for an identifier  on the
anti-clockwise unit circle Chord ring. Let 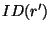 denote the identifier of the node 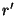 . Then, the probability that the distance between
identifiers  and 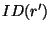 exceeds 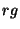 is given by Pr( 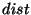 (  , 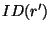 ) 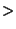 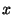 ) = 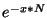 for some 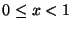 .
Given that when 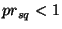 , there is small probability that an obfuscated
identifier is not safe, i.e., , there is small probability that an obfuscated
identifier is not safe, i.e., 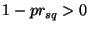 . We first discuss the motivation for detecting
and repairing unsafe obfuscations and then describe how to guarantee
good safety by our routing guard through a self-detection and
self-healing process. . We first discuss the motivation for detecting
and repairing unsafe obfuscations and then describe how to guarantee
good safety by our routing guard through a self-detection and
self-healing process.
We first motivate the need for ensuring safe obfuscations.
Let node  be the result of a lookup on identifier be the result of a lookup on identifier  and node and node 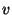 ( (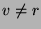 ) be the
result of a lookup on an unsafe obfuscated identifier ) be the
result of a lookup on an unsafe obfuscated identifier 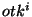 .
To perform a file read/write operation after locating the node that
stores the file .
To perform a file read/write operation after locating the node that
stores the file  , the user has to present the location
token , the user has to present the location
token  to node to node 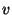 . If a user does
not check for unsafe obfuscation, then the file token . If a user does
not check for unsafe obfuscation, then the file token  would be exposed to some other node
would be exposed to some other node 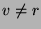 . If
node . If
node 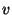 were malicious, then it could misuse the
capability were malicious, then it could misuse the
capability  to corrupt the file replica actually
stored at node to corrupt the file replica actually
stored at node  . .
We require a user to verify whether an obfuscated identifier is safe
or not using the following check: An obfuscated identifier 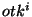 is considered safe if and only if is considered safe if and only if   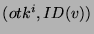 , where , where 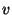 = = 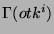 . By the definition of . By the definition of 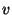 and and 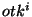 , we have , we have 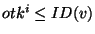 and and 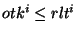 ( (
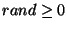 ). By ). By 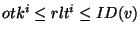 , node , node 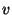 should be the immediate successor of the identifier
should be the immediate successor of the identifier  and thus be responsible for it. If the check failed, i.e.,
and thus be responsible for it. If the check failed, i.e., 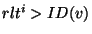 , then node , then node 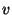 is definitely
not a successor of the identifier is definitely
not a successor of the identifier  . Hence, the
user can flag . Hence, the
user can flag 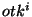 as an unsafe obfuscation of as an unsafe obfuscation of  . For example, referring Figure 3, . For example, referring Figure 3, 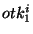 is safe
because, is safe
because,  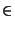 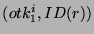 and and  = = 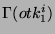 , and , and 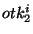 is unsafe
because, is unsafe
because,  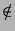 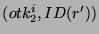 and and 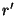 = = 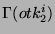 . .
When an obfuscated identifier is flagged as unsafe, the user needs
to retry the lookup operation with a new obfuscated identifier. This
retry process continues until max_retries rounds or until a
safe obfuscation is found. Since the probability of an unsafe
obfuscation is extremely small over multiple random choices of
obfuscated tokens (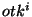 ), the call for retry rarely happens.
We also found from our experiments that the number of retries required
is almost always zero and seldom exceeds one. We believe that using max_retries
equal to two would suffice even in a highly conservative setting. Table
1 shows the expected number of
retries required for a lookup operation for different values of ), the call for retry rarely happens.
We also found from our experiments that the number of retries required
is almost always zero and seldom exceeds one. We believe that using max_retries
equal to two would suffice even in a highly conservative setting. Table
1 shows the expected number of
retries required for a lookup operation for different values of 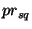 . .
6.4 Strength of Routing guard
The strength of a routing guard refers to its ability to counter lookup
sniffing based attacks. A typical lookup sniffing attack is called the range
sieving attack. Informally, in a range sieving attack, an adversary
sniffs lookup queries on the overlay network, and attempts to deduce
the actual identifier  from its multiple
obfuscated identifiers. We show that an adversary would have to expend from its multiple
obfuscated identifiers. We show that an adversary would have to expend 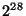 years to discover a replica location token years to discover a replica location token  even if it has observed even if it has observed 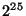 obfuscated
identifiers of obfuscated
identifiers of  . Note that . Note that 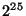 obfuscated
identifiers would be available to an adversary if the file replica obfuscated
identifiers would be available to an adversary if the file replica 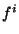 was accessed once a second for one full year by some
legal user of the file was accessed once a second for one full year by some
legal user of the file  . .
One can show that given multiple obfuscated identifiers it is
non-trivial for an adversary to categorize them into groups such that
all obfuscated identifiers in a group are actually obfuscations of one
identifier. To simplify the description of a range sieving attack, we
consider the worst case scenario where an adversary is capable of
categorizing obfuscated identifiers (say, based on their numerical
proximity).
We first concretely describe the range sieving attack assuming that 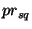 and and 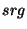 (from Theorem 6.1) are public knowledge. When an
adversary obtains an obfuscated identifier (from Theorem 6.1) are public knowledge. When an
adversary obtains an obfuscated identifier 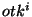 , the
adversary knows that the actual capability , the
adversary knows that the actual capability  is
definitely within the range is
definitely within the range 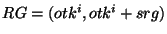 , where , where 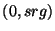 denotes a denotes a
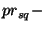 safe range. In fact, if obfuscations are uniformly
and randomly chosen from safe range. In fact, if obfuscations are uniformly
and randomly chosen from 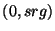 , then given an
obfuscated identifier , then given an
obfuscated identifier 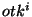 , the adversary knows nothing
more than the fact that the actual identifier , the adversary knows nothing
more than the fact that the actual identifier  could be uniformly and distributed over the range
could be uniformly and distributed over the range 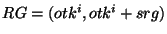 .
However, if a persistent adversary obtains multiple obfuscated
identifiers { .
However, if a persistent adversary obtains multiple obfuscated
identifiers {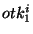 , , 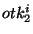 , ,  , , 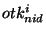 } that belong to the same target file, the
adversary can sieve the identifier space as follows. Let } that belong to the same target file, the
adversary can sieve the identifier space as follows. Let 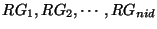 denote the ranges corresponding
to denote the ranges corresponding
to 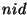 random obfuscations on the identifier random obfuscations on the identifier  . Then the capability of the target file is guaranteed
to lie in the sieved range . Then the capability of the target file is guaranteed
to lie in the sieved range 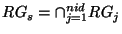 . Intuitively, if the number
of obfuscated identifiers ( . Intuitively, if the number
of obfuscated identifiers (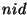 ) increases, the size of the
sieved range ) increases, the size of the
sieved range 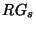 decreases. For all tokens decreases. For all tokens 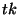 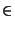 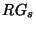 , the
likelihood that the obfuscated identifiers { , the
likelihood that the obfuscated identifiers {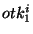 , , 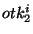 , , 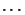 , , 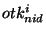 } are obfuscations of the identifier } are obfuscations of the identifier 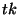 is equal. Hence, the adversary is left with no smart
strategy for searching the sieved range is equal. Hence, the adversary is left with no smart
strategy for searching the sieved range 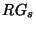 other than
performing a brute force attack on some random enumeration of
identifiers other than
performing a brute force attack on some random enumeration of
identifiers 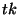  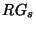 . .
Let ![$ E[RG_s]$](img135.png) denote the expected size of the
sieved range. Theorem 6.2 shows
that denote the expected size of the
sieved range. Theorem 6.2 shows
that ![$ E[RG_s] = \frac{srg}{nid}$](img136.png) . Hence, if the safe range . Hence, if the safe range 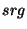 is significantly larger than is significantly larger than 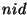 then the
routing guard can tolerate the range sieving attack. Recall the example
in Section 6 where then the
routing guard can tolerate the range sieving attack. Recall the example
in Section 6 where 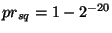 , , 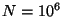 , the safe
range , the safe
range 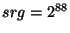 .
Suppose that a target file is accessed once per second for one year;
this results in .
Suppose that a target file is accessed once per second for one year;
this results in 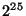 file accesses. An adversary who logs
all obfuscated identifiers over a year could sieve the range to about file accesses. An adversary who logs
all obfuscated identifiers over a year could sieve the range to about ![$ E[\vert RG_s\vert] = 2^{63}$](img139.png) . Assuming that the adversary
performs a brute force attack on the sieved range, by attempting a file
read operation at the rate of one read per millisecond, the adversary
would have tried . Assuming that the adversary
performs a brute force attack on the sieved range, by attempting a file
read operation at the rate of one read per millisecond, the adversary
would have tried 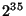 read operations per year. Thus, it
would take the adversary about read operations per year. Thus, it
would take the adversary about 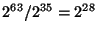 years to discover the actual file
identifier. For a detailed proof of Theorem 6.2 refer to our tech-report [23]. years to discover the actual file
identifier. For a detailed proof of Theorem 6.2 refer to our tech-report [23].
Table 1 summarizes the hardness
of breaking the obfuscation scheme for different values of 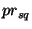 (minimum probability of safe obfuscation), assuming
that the adversary has logged (minimum probability of safe obfuscation), assuming
that the adversary has logged 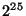 file
accesses (one access per second for one year) and that the nodes permit
at most one file access per millisecond. file
accesses (one access per second for one year) and that the nodes permit
at most one file access per millisecond.
Discussion. An interesting observation follows from the above
discussion: the amount of time taken to break the file identifier
obfuscation technique is almost independent of the number of attackers.
This is a desirable property. It implies that as the number of
attackers increases in the system, the hardness of breaking the file
capabilities will not decrease. The reason for location key based
systems to have this property is because the time taken for a brute
force attack on a file identifier is fundamentally limited by the rate
at which a hosting node permits accesses on files stored locally. On
the contrary, a brute force attack on a cryptographic key is inherently
parallelizable and thus becomes more powerful as the number of
attackers increases.
Theorem 6.2 Let 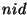 denote the number of obfuscated identifiers that
correspond to a target file. Let 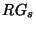 denote the
sieved range using the range sieving attack. Let 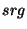
denote the maximum amount of obfuscation that could be 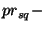 safely added to a file identifier. Then, the
expected size of range 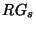 can be calculated by ![$ E[\vert RG_s\vert] = \frac{srg}{nid}$](img142.png) .
Inference attacks over location keys refer to those attacks wherein an
adversary attempts to infer the location of a file using indirect
techniques. We broadly classify inference attacks on location keys into
two categories: passive inference attacks and host
compromise based inference attacks. It is important to note that
none of the inference attacks described below would be effective in the
absence of collusion among malicious nodes.
Passive inference attacks refer to those attacks wherein an adversary
attempts to infer the location of a target file by passively observing
the overlay network. We studied two passive inference attacks on
location keys.
The lookup frequency inference attack is based on the ability of
malicious nodes to observe the frequency of lookup queries on the
overlay network. Assuming that the adversary knows the relative file
popularity, it can use the target file's lookup frequency to infer its
location. It has been observed that the general popularity of the web
pages accessed over the Internet follows a Zipf-like distribution [27]. An adversary may study the
frequency of file accesses by sniffing lookup queries and match the
observed file access frequency profile with a actual (pre-determined)
frequency profile to infer the location of a target file. This is
analogous to performing a frequency analysis attack on old symmetric
key ciphers like the Caesar's cipher [26].
The end-user IP-address inference attack is based on assumption that
the identity of the end-user can be inferred from its IP-address by an
overlay network node  , when the user requests node , when the user requests node  to perform a lookup on its behalf. A malicious node to perform a lookup on its behalf. A malicious node  could log and report this information to the adversary.
Recall that we have assumed that an adversary could be aware of the
owner and the legal users of a target file. Assuming that a user
accesses only a small subset of the total number of files on the
overlay network (including the target file) the adversary can narrow
down the set of nodes on the overlay network that may potentially hold
the target file. Note that this is a worst-case-assumption; in most
cases it may not possible to associate a user with one or a small
number IP-addresses (say, when the user obtains IP-address dynamically
(DHCP [2]) from a large ISP (Internet
Service Provider)). could log and report this information to the adversary.
Recall that we have assumed that an adversary could be aware of the
owner and the legal users of a target file. Assuming that a user
accesses only a small subset of the total number of files on the
overlay network (including the target file) the adversary can narrow
down the set of nodes on the overlay network that may potentially hold
the target file. Note that this is a worst-case-assumption; in most
cases it may not possible to associate a user with one or a small
number IP-addresses (say, when the user obtains IP-address dynamically
(DHCP [2]) from a large ISP (Internet
Service Provider)).
Host compromise based inference attacks require the adversary to
perform an active host compromise attack before it can infer the
location of a target file. We studied two host compromise based
inference attacks on location keys.
The file replica inference attack attempts to infer the identity of
a file from its contents; note that an adversary can reach the contents
of a file only after it compromises the file holder (unless the file
holder is malicious). The file  could be
encrypted to rule out the possibility of identifying a file from its
contents. Even when the replicas are encrypted, an adversary can
exploit the fact that all the replicas of file could be
encrypted to rule out the possibility of identifying a file from its
contents. Even when the replicas are encrypted, an adversary can
exploit the fact that all the replicas of file  are
identical. When an adversary compromises a good node, it can extract a
list of identifier and file content pairs (or a hash of the file
contents) stored at that node. Note that an adversary could perform a
frequency inference attack on the replicas stored at malicious nodes
and infer their filenames. Hence, if an adversary were to obtain the
encrypted contents of one of the replicas of a target file are
identical. When an adversary compromises a good node, it can extract a
list of identifier and file content pairs (or a hash of the file
contents) stored at that node. Note that an adversary could perform a
frequency inference attack on the replicas stored at malicious nodes
and infer their filenames. Hence, if an adversary were to obtain the
encrypted contents of one of the replicas of a target file  , it could examine the extracted list of identifiers and
file contents to obtain the identities of other replicas. Once, the
adversary has the locations of , it could examine the extracted list of identifiers and
file contents to obtain the identities of other replicas. Once, the
adversary has the locations of 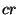 copies of a
file copies of a
file  , the , the  could be
attacked easily. This attack is especially more plausible on read-only
files since their contents do not change over a long period of time. On
the other hand, the update frequency on read-write files might guard
them file replica inference attack. could be
attacked easily. This attack is especially more plausible on read-only
files since their contents do not change over a long period of time. On
the other hand, the update frequency on read-write files might guard
them file replica inference attack.
File size inference attack is based on the assumption that an
adversary might be aware of the target file's size. Malicious nodes
(and compromised nodes) report the size of the files stored at them to
an adversary. If the size of files stored on the overlay network
follows a skewed distribution, the adversary would be able to identify
the target file (much like the lookup frequency inference attack).
For a detailed discussion on inference attacks and techniques to
curb them please refer to our technical report [23]. Identifying other potential
inference attacks and developing defenses against them is a part of our
ongoing work.
7.3 Location Rekeying
In addition to the inference attacks listed above, there could be other
possible inference attacks on a LocationGuard based file system. In due
course of time, the adversary might be able to gather enough
information to infer the location of a target file. Location rekeying
is a general defense against both known and unknown inference
attacks. Users can periodically choose new location keys so as to
render all past inferences made by an adversary useless.
In order to secure the system from Biham's key collision attacks [4], one may associate an initialization
vector (IV) with the location key and change IV rather than the
location key itself.
Location rekeying is analogous to rekeying of cryptographic keys.
Unfortunately, rekeying is an expensive operation: rekeying
cryptographic keys requires data to be re-encrypted; rekeying location
keys requires files to be relocated on the overlay network. Hence, it
is important to keep the rekeying frequency small enough to reduce
performance overheads and large enough to secure files on the overlay
network. In our experiments section, we estimate the periodicity with
which location keys have to be changed in order to reduce the
probability of an attack on a target file.
8 Discussion
In this section, we briefly discuss a number of issues related to
security, distribution and management of LocationGuard.
Key Security. We have assumed that in LocationGuard based
file systems it is the responsibility of the legal users to secure
location keys from an adversary. If a user has to access thousands of
files then the user must be responsible for the secrecy of thousands of
location keys. One viable solution could be to compile all location
keys into one key-list file, encrypt the file and store it on
the overlay network. The user now needs to keep secret only one
location key that corresponds to the key-list. This 128-bit
location key could be physically protected using tamper-proof hardware
devices, smartcards, etc.
Key Distribution. Secure distribution of keys has been a
major challenge in large scale distributed systems. The problem of
distributing location keys is very similar to that of distributing
cryptographic keys. Typically, keys are distributed using out-of-band
techniques. For instance, one could use PGP [18]
based secure email service to transfer location keys from a file owner
to file users.
Key Management. Managing location keys efficiently becomes an
important issue when (i) an owner owns several thousand files, and (ii)
the set of legal users for a file vary significantly over time. In the
former scenario, the file owner could reduce the key management cost by
assigning one location key for a group of files. Any user who obtains
the location key for a file  would implicitly be authorized
to access the group of files to which would implicitly be authorized
to access the group of files to which  belong. However,
the later scenario may seriously impede the system's performance in
situations where it may require location key to be changed each time
the group membership changes. belong. However,
the later scenario may seriously impede the system's performance in
situations where it may require location key to be changed each time
the group membership changes.
The major overhead for LocationGuard arises from key distribution
and key management. Also, location rekeying could be an important
factor. Key security, distribution and management in LocationGuard
using group key management protocols [11]
are a part of our ongoing research work.
Other issues that are not discussed in this paper include the
problem of a valid user illegally distributing the capabilities
(tokens) to an adversary, and the robustness of the lookup protocol and
the overlay network in the presence of malicious nodes. In this paper
we assume that all valid users are well behaved and the lookup protocol
is robust. Readers may refer to [24]
for detailed discussion on the robustness of lookup protocols on DHT
based overlay networks.
9 Experimental Evaluation
In this section, we report results from our simulation based
experiments to evaluate the LocationGuard approach for building secure
wide-area network file systems. We implemented our simulator using a
discrete event simulation [8] model, and
implemented the Chord lookup protocol [25]
on the overlay network compromising of 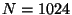 nodes. In
all experiments reported in this paper, a random nodes. In
all experiments reported in this paper, a random 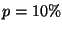 of of 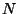 nodes are chosen to behave
maliciously. We set the number of replicas of a file to be nodes are chosen to behave
maliciously. We set the number of replicas of a file to be 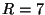 and vary the corruption threshold and vary the corruption threshold 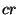 in
our experiments. We simulated the bad nodes as having large but bounded
power based on the parameters in
our experiments. We simulated the bad nodes as having large but bounded
power based on the parameters 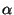 (DoS attack
strength), (DoS attack
strength), 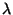 (node compromise rate) and (node compromise rate) and 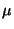 (node recovery rate) (see the threat model in Section 3). We study the cost of using
location key technique by quantifying the overhead of using location
keys and evaluate the benefits of the location key technique by
measuring the effectiveness of location keys against DoS and host
compromise based target file attacks.
Operational Overhead. We first quantify the performance and
storage overheads incurred by location keys. All measurements presented
in this section were obtained on a 900 MHz Intel Pentium III processor
running RedHat Linux 9.0. Let us consider a typical file read/write
operation. The operation consists of the following steps: (i) generate
the file replica identifiers, (ii) lookup the replica holders on the
overlay network, and (iii) process the request at replica holders. Step
(i) requires computations using the keyed-hash function with location
keys, which otherwise would have required computations using a normal
hash function. We found that the computation time difference between
HMAC-MD5 (a keyed-hash function) and MD5 (normal hash function) is
negligibly small (order of a few microseconds) using the standard
OpenSSL library [17]. Step (ii)
involves a pseudo-random number generation (few microseconds using the
OpenSSL library) and may require lookups to be retried in the event
that the obfuscated identifier turns out to be unsafe. Given that
unsafe obfuscations are extremely rare (see Table 1) retries are only required
occasionally and thus this overhead is negligible. Step (iii) adds no
overhead because our access check is almost free. As long as the user
can present the correct filename (token), the replica holder would
honor a request on that file. (node recovery rate) (see the threat model in Section 3). We study the cost of using
location key technique by quantifying the overhead of using location
keys and evaluate the benefits of the location key technique by
measuring the effectiveness of location keys against DoS and host
compromise based target file attacks.
Operational Overhead. We first quantify the performance and
storage overheads incurred by location keys. All measurements presented
in this section were obtained on a 900 MHz Intel Pentium III processor
running RedHat Linux 9.0. Let us consider a typical file read/write
operation. The operation consists of the following steps: (i) generate
the file replica identifiers, (ii) lookup the replica holders on the
overlay network, and (iii) process the request at replica holders. Step
(i) requires computations using the keyed-hash function with location
keys, which otherwise would have required computations using a normal
hash function. We found that the computation time difference between
HMAC-MD5 (a keyed-hash function) and MD5 (normal hash function) is
negligibly small (order of a few microseconds) using the standard
OpenSSL library [17]. Step (ii)
involves a pseudo-random number generation (few microseconds using the
OpenSSL library) and may require lookups to be retried in the event
that the obfuscated identifier turns out to be unsafe. Given that
unsafe obfuscations are extremely rare (see Table 1) retries are only required
occasionally and thus this overhead is negligible. Step (iii) adds no
overhead because our access check is almost free. As long as the user
can present the correct filename (token), the replica holder would
honor a request on that file.
Now, let us compare the storage overhead at the users and the nodes
that are a part of the overlay network. Users need to store only an
additional 128-bit location key (16 Bytes) along with other file
meta-data for each file they want to access. Even a user who uses 1
million files on the overlay network needs to store only an additional
16MBytes of location keys. Further, there is no extra storage overhead
on the rest of the nodes on the overlay network. For a detailed
description of our implementation of LocationGuard and benchmark
results for file read and write operations refer to our tech-report [23].
Figure 4:
Probability of a Target File Attack for 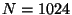 nodes and nodes and 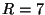 using DoS Attack using DoS Attack
![\includegraphics[width=\linewidth]{fig/pr-dos.eps}](img144.png)
|
Figure 5:
Probability of a Target File Attack for 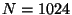 nodes and nodes and 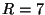 using Host Compromise Attack (with no token collection) using Host Compromise Attack (with no token collection)
|
|
Figure 6: Probability of a
Target File Attack for 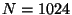 nodes and nodes and 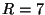 using Host Compromise Attack with token collection from compromised
nodes
using Host Compromise Attack with token collection from compromised
nodes
|
|
Denial of Service Attacks. Figure 4
shows the probability of an attack for varying 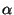 and different values of corruption threshold (
and different values of corruption threshold (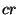 ).
Without the knowledge of the location of file replicas an adversary is
forced to attack (DoS) a random collection of nodes in the system and hope
that that at least ).
Without the knowledge of the location of file replicas an adversary is
forced to attack (DoS) a random collection of nodes in the system and hope
that that at least 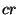 replicas of the target file is
attacked. Observe that if the malicious nodes are more powerful (larger replicas of the target file is
attacked. Observe that if the malicious nodes are more powerful (larger
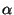 ) or if the corruption threshold ) or if the corruption threshold 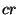 is
very low with respect to the size ( is
very low with respect to the size (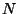 ) of the network,
then the probability of an attack is higher. If an adversary were aware
of the ) of the network,
then the probability of an attack is higher. If an adversary were aware
of the 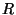 replica holders of a target file then a
weak collection of replica holders of a target file then a
weak collection of 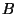 malicious nodes, such as malicious nodes, such as  (i.e., 10% of (i.e., 10% of  ) with ) with 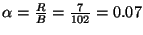 , can easily
attack the target file. It is also true that for a file system to
handle the DoS attacks on a file with , can easily
attack the target file. It is also true that for a file system to
handle the DoS attacks on a file with  , it would require a large number of replicas ( , it would require a large number of replicas ( close to close to  ) to be maintained for each file.
For example, in the case where ) to be maintained for each file.
For example, in the case where  and and 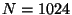 , the
system needs to maintain as large as 100+ replicas for each file.
Clearly, without location keys, the effort required for an adversary to
attack a target file (i.e., make it unavailable) is dependent only on , the
system needs to maintain as large as 100+ replicas for each file.
Clearly, without location keys, the effort required for an adversary to
attack a target file (i.e., make it unavailable) is dependent only on  , but is independent of the number of good nodes ( , but is independent of the number of good nodes ( ) in the system. On the contrary, the location key based
techniques scale the hardness of an attack with the number of good
nodes in the system. Thus even with a very small ) in the system. On the contrary, the location key based
techniques scale the hardness of an attack with the number of good
nodes in the system. Thus even with a very small  , the
location key based system can make it very hard for any adversary to
launch a targeted file attack. , the
location key based system can make it very hard for any adversary to
launch a targeted file attack.
Host Compromise Attacks. To further evaluate the
effectiveness of location keys against targeted file attacks, we
evaluate location keys against host compromise attacks. Our first
experiment on host compromise attack shows the probability of an attack
on the target file assuming that the adversary can not collect
capabilities (tokens) stored at the compromised nodes. Hence, the
target file is attacked if 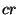 or more of its replicas are
stored at either malicious nodes or compromised nodes. Figure 5 shows the probability of an attack
for different values of corruption threshold ( or more of its replicas are
stored at either malicious nodes or compromised nodes. Figure 5 shows the probability of an attack
for different values of corruption threshold (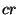 )
and varying )
and varying 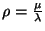 (measured in number of node
recoveries per node compromise). We ran the simulation for a duration
of (measured in number of node
recoveries per node compromise). We ran the simulation for a duration
of 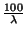 time units. Recall that
time units. Recall that 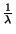 denotes the mean time required for one
malicious node to compromise a good node. Note that if the simulation
were run for infinite time then the probability of attack is always
one. This is because, at some point in time, denotes the mean time required for one
malicious node to compromise a good node. Note that if the simulation
were run for infinite time then the probability of attack is always
one. This is because, at some point in time, 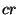 or
more replicas of a target file would be assigned to malicious nodes (or
compromised nodes) in the system. or
more replicas of a target file would be assigned to malicious nodes (or
compromised nodes) in the system.
From Figure 5 we observe that
when 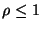 , the
system is highly vulnerable since the node recovery rate is lower than
the node compromise rate. Note that while a DoS attack could tolerate
powerful malicious nodes ( , the
system is highly vulnerable since the node recovery rate is lower than
the node compromise rate. Note that while a DoS attack could tolerate
powerful malicious nodes (
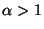 ), the host compromise attack cannot tolerate the
situation where the node compromise rate is higher than their recovery
rate ( ), the host compromise attack cannot tolerate the
situation where the node compromise rate is higher than their recovery
rate (
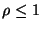 ). This is primarily because of the cascading
effect of host compromise attack. The larger the number of compromised
nodes we have, the higher is the rate at which other good nodes are
compromised (see the adversary model in Section 3). Table 2 shows the mean fraction of good
nodes ( ). This is primarily because of the cascading
effect of host compromise attack. The larger the number of compromised
nodes we have, the higher is the rate at which other good nodes are
compromised (see the adversary model in Section 3). Table 2 shows the mean fraction of good
nodes ( ) that are in an uncompromised state
for different values of ) that are in an uncompromised state
for different values of 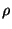 . Observe from Table 2 that when . Observe from Table 2 that when 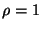 , most of the good nodes are in compromised state. , most of the good nodes are in compromised state.
 |
0.5
|
1.0
|
1.1
|
1.2
|
1.5
|
3.0
|
 |
0
|
0
|
0.06
|
0.44
|
0.77
|
0.96
|
Table 2: Mean Fraction of Good
Nodes in Uncompromised State (  )
As we have mentioned in Section 4.3, the adversary could
collect the capabilities (tokens) of the file replicas stored at
compromised nodes; these tokens can be used by the adversary at any
point in future to corrupt these replicas using a simple write
operation. Hence, our second experiment on host compromise attack
measures the probability of a attack assuming that the adversary
collects the file tokens stored at compromised nodes. Figure 6 shows the mean effort required to
locate all the replicas of a target file (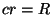 ). The
effort required is expressed in terms of the fraction of good that need
to be compromised by the adversary to attack the target file. ). The
effort required is expressed in terms of the fraction of good that need
to be compromised by the adversary to attack the target file.
Note that in the absence of location keys, an adversary needs to
compromise at most 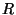 good nodes in order to succeed a
targeted file attack. Clearly, location key based techniques increase
the required effort by several orders of magnitude. For instance, when good nodes in order to succeed a
targeted file attack. Clearly, location key based techniques increase
the required effort by several orders of magnitude. For instance, when 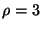 , an adversary has to compromise 70% of the good
nodes in the system in order to attain the probability of an attack to
a nominal value of , an adversary has to compromise 70% of the good
nodes in the system in order to attain the probability of an attack to
a nominal value of 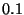 , even under the assumption
that an adversary collects file capabilities from compromised nodes. If
an adversary compromises every good node in the system once, it gets to
know the tokens of all files stored on the overlay network. In Section 7.3 we had proposed location re-keying
to protect the file system from such attacks. The exact period of
location re-keying can be derived from Figure 6. For instance, when , even under the assumption
that an adversary collects file capabilities from compromised nodes. If
an adversary compromises every good node in the system once, it gets to
know the tokens of all files stored on the overlay network. In Section 7.3 we had proposed location re-keying
to protect the file system from such attacks. The exact period of
location re-keying can be derived from Figure 6. For instance, when 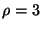 , if a user wants to retain the attack probability
below 0.1, the time interval between re-keying should equal the amount
of time it takes for an adversary to compromise 70% of the good nodes
in the system. Table 3 shows the
time taken (normalized by , if a user wants to retain the attack probability
below 0.1, the time interval between re-keying should equal the amount
of time it takes for an adversary to compromise 70% of the good nodes
in the system. Table 3 shows the
time taken (normalized by 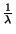 ) for an adversary to increase the attack
probability on a target file to 0.1 for different values of ) for an adversary to increase the attack
probability on a target file to 0.1 for different values of 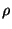 . Observe that as . Observe that as 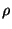 increases,
location re-keying can be more and more infrequent. increases,
location re-keying can be more and more infrequent.
 |
0.5
|
1.0
|
1.1
|
1.2
|
1.5
|
3.0
|
Re-Keying
Interval
|
0
|
0
|
0.43
|
1.8
|
4.5
|
6.6
|
Table 3: Time Interval Between
Location Re-Keying (normalized by  time units)
Lookup Guard. We performed the following experiments on our lookup
identifier obfuscation technique (see Section 6): (i) studied the effect of
obfuscation range on the probability of a safe obfuscation, (ii)
measured the number of lookup retries, and (iii) measured the expected
size of the sieved range (using the range sieving attack). We found
that a safe range for identifier obfuscation is very large even for
large values of 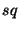 (very close to 1); we observed that
number of lookup retries is almost zero and seldom exceeds one; we
found that the size of the sieved range is too large to attempt a brute
force attack even if file accesses over one full year were logged.
Finally, our experimental results very closely match the analytical
results shown in Table 1. For more
details on our experimental results refer to our tech-report [23]. (very close to 1); we observed that
number of lookup retries is almost zero and seldom exceeds one; we
found that the size of the sieved range is too large to attempt a brute
force attack even if file accesses over one full year were logged.
Finally, our experimental results very closely match the analytical
results shown in Table 1. For more
details on our experimental results refer to our tech-report [23].
10 Related Work
Serverless distributed file systems like CFS [7],
Farsite [1], OceanStore [15] and SiRiUS [10] have received significant attention
from both the industry and the research community. These file systems
store files on a large collection of untrusted nodes that form an
overlay network. They use cryptographic techniques to ensure file data
confidentiality and integrity. Unfortunately, cryptographic techniques
cannot protect a file holder from DoS or host compromise attacks.
LocationGuard presents low overhead and highly effective techniques to
guard a distributed file system from such targeted file attacks.
The secure Overlay Services (SOS) paper [13]
describes an architecture that proactively prevents DoS attacks using
secure overlay tunneling and routing via consistent hashing. However,
the assumptions and the applications in [13]
are noticeably different from that of ours. For example, the SOS paper
uses the overlay network for introducing randomness and anonymity into
the SOS architecture to make it difficult for malicious nodes to attack
target applications of interest. LocationGuard techniques treat the
overlay network as a part of the target applications we are interested
in and introduce randomness and anonymity through location key based
hashing and lookup based file identifier obfuscation, making it
difficult for malicious nodes to target their attacks on a small subset
of nodes in the system, who are the replica holders of the target file
of interest.
The Hydra OS [6], [22] proposed a capability-based file
access control mechanism. LocationGuard can be viewed as an
implementation of capability-based access control on a wide-area
network. The most important challenge for LocationGuard is that of
keeping a file's capability secret and yet being able to perform a
lookup on it (see Section 6).
Indirect attacks such as attempts to compromise cryptographic keys
from the system administrator or use fault attacks like RSA timing
attacks, glitch attacks, hardware and software implementation bugs [5] have been the most popular
techniques to attack cryptographic algorithms. Similarly, attackers
might resort to inference attacks on LocationGuard since a brute force
attack (even with range sieving) on location keys is highly infeasible.
Due to space restrictions we have not been able to include location
inference guards in this paper. For details on location inference
guards, refer to our tech-report [23].
11 Conclusion
In this paper we have proposed LocationGuard for securing wide area
serverless file sharing systems from targeted file attacks. Analogous
to traditional cryptographic keys that hide the contents of a file,
LocationGuard hide the location of a file on an overlay network.
LocationGuard retains traditional cryptographic guarantees like file
data confidentiality and integrity. In addition, LocationGuard guards a
target file from DoS and host compromise attacks, provides a simple and
efficient access control mechanism and adds minimal performance and
storage overhead to the system. We presented experimental results that
demonstrate the effectiveness of our techniques against targeted file
attacks. In conclusion, LocationGuard mechanisms make it possible to
build simple and secure wide-area network file systems.
Acknowledgements
This research is partially supported by NSF CNS, NSF ITR, IBM SUR
grant, and HP Equipment Grant. Any opinions, findings, and conclusions
or recommendations expressed in the project material are those of the
authors and do not necessarily reflect the views of the sponsors.
-
- 1
- A. Adya, W. Bolosky, M. Castro, G. Cermak,
R. Chaiken, J. R. Douceur, J. Howell, J. R. Lorch,
M. Theimer, and R. P. Wattenhofer.
Farsite: Federated, available and reliable storage for an incompletely
trusted environment.
In Proceedings of the 5th International Symposium on OSDI,
2002.
- 2
- I. R. Archives.
RFC 2131: Dynamic host configuration protocol.
http://www.faqs.org/rfcs/rfc2131.html.
- 3
- J. K. B. Zhao and A. Joseph.
Tapestry: An infrastructure for fault-tolerance wide-area location and
routing.
Technical Report UCB/CSD-01-1141, University of California, Berkeley,
2001.
- 4
- E. Biham.
How to decrypt or even substitute DES-encrypted messages in 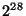 steps. steps.
In Information Processing Letters, 84, 2002.
- 5
- D. Boneh and D. Brumley.
Remote timing attacks are practical.
In Proceedings of the 12th USENIX Security Symposium, 2003.
- 6
- E. Cohen and D. Jefferson.
Protection in the hydra operating system.
In Proceeding of the ACM Symposium on Operating Systems Principles,
1975.
- 7
- F. Dabek, M. F. Kaashoek, D. Karger,
R. Morris, and I. Stoica.
Wide-area cooperative storage with CFS.
In Proceedings of the 18th ACM SOSP, October 2001.
- 8
- FIPS.
Data encryption standard (DES).
http://www.itl.nist.gov/fipspubs/fip46-2.htm.
- 9
- Gnutella.
The gnutella home page.
http://gnutella.wego.com/.
- 10
- E. J. Goh, H. Shacham, N. Modadugu, and
D. Boneh.
SiRiUS: Securing remote untrusted storage.
In Proceedings of NDSS, 2003.
- 11
- H. Harney and C. Muckenhirn.
Group key management protocol (GKMP) architecture.
http://www.rfc-archive.org/getrfc.php?rfc=2094.
- 12
- T. Jaeger and A. D. Rubin.
Preserving integrity in remote file location and retrieval.
In Proceedings of NDSS, 1996.
- 13
- A. Keromytis, V. Misra, and D. Rubenstein.
SOS: Secure overlay services.
In Proceedings of the ACM SIGCOMM, 2002.
- 14
- H. Krawczyk, M. Bellare, and R. Canetti.
RFC 2104 - HMAC: Keyed-hashing for message authentication.
http://www.faqs.org/rfcs/rfc2104.html.
- 15
- J. Kubiatowics, D. Bindel, Y. Chen,
S. Czerwinski, P. Eaton, D. Geels, R. Gummadi,
S. Rhea, H. Weatherspoon, W. Weimer, C. Wells, and
B. Zhao.
OceanStore: An architecture for global-scale persistent storage.
In Proceedings of the 9th International Conference on
Architectural Support for Programming Languages and Operating Systems,
November 2000.
- 16
- NIST.
AES: Advanced encryption standard.
http://csrc.nist.gov/CryptoToolkit/aes/.
- 17
- OpenSSL.
OpenSSL: The open source toolkit for ssl/tls.
http://www.openssl.org/.
- 18
- PGP.
Pretty good privacy.
http://www.pgp.com/.
- 19
- S. Ratnasamy, P. Francis, M. Handley,
R. Karp, and S. Shenker.
A scalable content-addressable network.
In Proceedings of SIGCOMM Annual Conference on Data Communication,
Aug 2001.
- 20
- A. Rowstron and P. Druschel.
Pastry: Scalable, distributed object location and routing for
large-scale peer-to-peer systems.
In Proceedings of the 18th IFIP/ACM International Conference on
Distributed Systems Platforms (Middleware 2001), Nov 2001.
- 21
- RSA.
RSA security - public-key cryptography standards (pkcs).
http://www.rsasecurity.com/rsalabs/pkcs/.
- 22
- J. S. Shapiro, J. M. Smith, and D. J. Farber.
EROS: A fast capability system.
In Proceedings of 17th ACM Symposium on Operating Systems
Principles, 1999.
- 23
- M. Srivatsa and L. Liu.
Countering targeted file attacks using location keys.
Technical Report GIT-CERCS-04-31, Georgia Institute of Technology,
2004.
- 24
- M. Srivatsa and L. Liu.
Vulnerabilities and security issues in structured overlay networks: A
quantitative analysis.
In Proceedings of the Annual Computer Security Applications
Conference (ACSAC), 2004.
- 25
- I. Stoica, R. Morris, D. Karger, M. Kaashoek,
and H. Balakrishnan.
Chord: A scalable peer-to-peer lookup service for internet
applications.
In Proceedings of SIGCOMM Annual Conference on Data Communication,
August 2001.
- 26
- M. World.
The caesar cipher.
http://www.mathworld.com.
- 27
- L. Xiong and L. Liu.
Peertrust: Supporting reputation-based trust for peer-to-peer
electronic communities.
In Proceedings of IEEE TKDE, Vol. 16, No. 7, 2004.
  
Mudhakar Srivatsa
2005-04-29
|

![\includegraphics[width=\linewidth]{fig/perturb.eps}](img64.png)
![]() for a given
replica location token
for a given
replica location token ![]() . We say that an obfuscated
identifier
. We say that an obfuscated
identifier ![]() is a safe obfuscation of identifier
is a safe obfuscation of identifier ![]() if and only if a lookup on both
if and only if a lookup on both ![]() and
and ![]() result in the same physical node
result in the same physical node ![]() . For example, in Figure 3,
identifier
. For example, in Figure 3,
identifier ![]() is a safe obfuscation of identifier
is a safe obfuscation of identifier ![]() (
(
![]() =
= ![]() =
= ![]() ), while identifier
), while identifier ![]() is unsafe (
is unsafe (
![]() =
= ![]()
![]()
![]() ).
).
![]() as a set of all identifiers
in the range (
as a set of all identifiers
in the range (![]() ,
, ![]() ), where
), where ![]() denotes a safe obfuscation range (
denotes a safe obfuscation range (
![]() . When a user intends to query for a replica
location token
. When a user intends to query for a replica
location token ![]() , the user actually performs a lookup
on an obfuscated identifier
, the user actually performs a lookup
on an obfuscated identifier ![]() =
= ![]() =
= ![]()
![]()
![]() . The function
. The function ![]() returns a number chosen uniformly and
randomly in the range
returns a number chosen uniformly and
randomly in the range ![]() .
. ![]() such that:
such that:![]() .
.![]() } it is very hard for an adversary to guess the actual
identifier
} it is very hard for an adversary to guess the actual
identifier ![]() .
. ![]() (
(![]() ,
, ![]() )
) ![]()
![]() ) =
) = ![]() , where
, where ![]() denotes the number of nodes on
the overlay network and
denotes the number of nodes on
the overlay network and ![]() denotes any value satisfying
denotes any value satisfying ![]() . Informally, the theorem states that the
probability that the predecessor node
. Informally, the theorem states that the
probability that the predecessor node ![]() is
further away from the identifier
is
further away from the identifier ![]() decreases
exponentially with the distance. For a detailed proof please refer to
our tech-report [23].
decreases
exponentially with the distance. For a detailed proof please refer to
our tech-report [23].
![]() is safe with
respect to
is safe with
respect to ![]() if
if ![]() (
(![]() ,
, ![]() )
) ![]()
![]() , the
probability that a obfuscation
, the
probability that a obfuscation ![]() is safe can
be calculated using
is safe can
be calculated using ![]() .
.
![]() as follows. We first use
as follows. We first use ![]() to obtain an upper bound on
to obtain an upper bound on ![]() :
By
:
By ![]()
![]()
![]() , we have,
, we have, ![]()
![]()
![]() . Hence, if
. Hence, if ![]() is chosen from a safe range
is chosen from a safe range ![]() , where
, where ![]() =
= ![]() , then all obfuscations are
guaranteed to be safe with a probability greater than or equal to
, then all obfuscations are
guaranteed to be safe with a probability greater than or equal to ![]() .
.
![]() and
and ![]() million
nodes,
million
nodes, ![]() . Hence, on a
128-bit Chord ring
. Hence, on a
128-bit Chord ring ![]() could be chosen from a range
of size
could be chosen from a range
of size ![]() . Table 1 shows the size of a
. Table 1 shows the size of a ![]() safe obfuscation range
safe obfuscation range ![]() for different
values of
for different
values of ![]() . Observe that if we set
. Observe that if we set ![]() , then
, then ![]() =
= ![]() = 0. Hence, if we want 100%
safety, the obfuscation range
= 0. Hence, if we want 100%
safety, the obfuscation range ![]() must be zero,
i.e., the token
must be zero,
i.e., the token ![]() cannot be obfuscated.
cannot be obfuscated.
![]() be the result of a lookup on identifier
be the result of a lookup on identifier ![]() and node
and node ![]() (
(![]() ) be the
result of a lookup on an unsafe obfuscated identifier
) be the
result of a lookup on an unsafe obfuscated identifier ![]() .
To perform a file read/write operation after locating the node that
stores the file
.
To perform a file read/write operation after locating the node that
stores the file ![]() , the user has to present the location
token
, the user has to present the location
token ![]() to node
to node ![]() . If a user does
not check for unsafe obfuscation, then the file token
. If a user does
not check for unsafe obfuscation, then the file token ![]() would be exposed to some other node
would be exposed to some other node ![]() . If
node
. If
node ![]() were malicious, then it could misuse the
capability
were malicious, then it could misuse the
capability ![]() to corrupt the file replica actually
stored at node
to corrupt the file replica actually
stored at node ![]() .
.
![]() is considered safe if and only if
is considered safe if and only if ![]()
![]()
![]() , where
, where ![]() =
= ![]() . By the definition of
. By the definition of ![]() and
and ![]() , we have
, we have ![]() and
and ![]() (
(
![]() ). By
). By ![]() , node
, node ![]() should be the immediate successor of the identifier
should be the immediate successor of the identifier ![]() and thus be responsible for it. If the check failed, i.e.,
and thus be responsible for it. If the check failed, i.e., ![]() , then node
, then node ![]() is definitely
not a successor of the identifier
is definitely
not a successor of the identifier ![]() . Hence, the
user can flag
. Hence, the
user can flag ![]() as an unsafe obfuscation of
as an unsafe obfuscation of ![]() . For example, referring Figure 3,
. For example, referring Figure 3, ![]() is safe
because,
is safe
because, ![]()
![]()
![]() and
and ![]() =
= ![]() , and
, and ![]() is unsafe
because,
is unsafe
because, ![]()
![]()
![]() and
and ![]() =
= ![]() .
.
![]() ), the call for retry rarely happens.
We also found from our experiments that the number of retries required
is almost always zero and seldom exceeds one. We believe that using max_retries
equal to two would suffice even in a highly conservative setting. Table
1 shows the expected number of
retries required for a lookup operation for different values of
), the call for retry rarely happens.
We also found from our experiments that the number of retries required
is almost always zero and seldom exceeds one. We believe that using max_retries
equal to two would suffice even in a highly conservative setting. Table
1 shows the expected number of
retries required for a lookup operation for different values of ![]() .
. ![]() and
and ![]() (from Theorem 6.1) are public knowledge. When an
adversary obtains an obfuscated identifier
(from Theorem 6.1) are public knowledge. When an
adversary obtains an obfuscated identifier ![]() , the
adversary knows that the actual capability
, the
adversary knows that the actual capability ![]() is
definitely within the range
is
definitely within the range ![]() , where
, where ![]() denotes a
denotes a
![]() safe range. In fact, if obfuscations are uniformly
and randomly chosen from
safe range. In fact, if obfuscations are uniformly
and randomly chosen from ![]() , then given an
obfuscated identifier
, then given an
obfuscated identifier ![]() , the adversary knows nothing
more than the fact that the actual identifier
, the adversary knows nothing
more than the fact that the actual identifier ![]() could be uniformly and distributed over the range
could be uniformly and distributed over the range ![]() .
However, if a persistent adversary obtains multiple obfuscated
identifiers {
.
However, if a persistent adversary obtains multiple obfuscated
identifiers {![]() ,
, ![]() ,
, ![]() ,
, ![]() } that belong to the same target file, the
adversary can sieve the identifier space as follows. Let
} that belong to the same target file, the
adversary can sieve the identifier space as follows. Let ![]() denote the ranges corresponding
to
denote the ranges corresponding
to ![]() random obfuscations on the identifier
random obfuscations on the identifier ![]() . Then the capability of the target file is guaranteed
to lie in the sieved range
. Then the capability of the target file is guaranteed
to lie in the sieved range ![]() . Intuitively, if the number
of obfuscated identifiers (
. Intuitively, if the number
of obfuscated identifiers (![]() ) increases, the size of the
sieved range
) increases, the size of the
sieved range ![]() decreases. For all tokens
decreases. For all tokens ![]()
![]()
![]() , the
likelihood that the obfuscated identifiers {
, the
likelihood that the obfuscated identifiers {![]() ,
, ![]() ,
, ![]() ,
, ![]() } are obfuscations of the identifier
} are obfuscations of the identifier ![]() is equal. Hence, the adversary is left with no smart
strategy for searching the sieved range
is equal. Hence, the adversary is left with no smart
strategy for searching the sieved range ![]() other than
performing a brute force attack on some random enumeration of
identifiers
other than
performing a brute force attack on some random enumeration of
identifiers ![]()
![]()
![]() .
.
![]() denote the expected size of the
sieved range. Theorem 6.2 shows
that
denote the expected size of the
sieved range. Theorem 6.2 shows
that ![]() . Hence, if the safe range
. Hence, if the safe range ![]() is significantly larger than
is significantly larger than ![]() then the
routing guard can tolerate the range sieving attack. Recall the example
in Section 6 where
then the
routing guard can tolerate the range sieving attack. Recall the example
in Section 6 where ![]() ,
, ![]() , the safe
range
, the safe
range ![]() .
Suppose that a target file is accessed once per second for one year;
this results in
.
Suppose that a target file is accessed once per second for one year;
this results in ![]() file accesses. An adversary who logs
all obfuscated identifiers over a year could sieve the range to about
file accesses. An adversary who logs
all obfuscated identifiers over a year could sieve the range to about ![]() . Assuming that the adversary
performs a brute force attack on the sieved range, by attempting a file
read operation at the rate of one read per millisecond, the adversary
would have tried
. Assuming that the adversary
performs a brute force attack on the sieved range, by attempting a file
read operation at the rate of one read per millisecond, the adversary
would have tried ![]() read operations per year. Thus, it
would take the adversary about
read operations per year. Thus, it
would take the adversary about ![]() years to discover the actual file
identifier. For a detailed proof of Theorem 6.2 refer to our tech-report [23].
years to discover the actual file
identifier. For a detailed proof of Theorem 6.2 refer to our tech-report [23].
![]() (minimum probability of safe obfuscation), assuming
that the adversary has logged
(minimum probability of safe obfuscation), assuming
that the adversary has logged ![]() file
accesses (one access per second for one year) and that the nodes permit
at most one file access per millisecond.
file
accesses (one access per second for one year) and that the nodes permit
at most one file access per millisecond.
![]() , when the user requests node
, when the user requests node ![]() to perform a lookup on its behalf. A malicious node
to perform a lookup on its behalf. A malicious node ![]() could log and report this information to the adversary.
Recall that we have assumed that an adversary could be aware of the
owner and the legal users of a target file. Assuming that a user
accesses only a small subset of the total number of files on the
overlay network (including the target file) the adversary can narrow
down the set of nodes on the overlay network that may potentially hold
the target file. Note that this is a worst-case-assumption; in most
cases it may not possible to associate a user with one or a small
number IP-addresses (say, when the user obtains IP-address dynamically
(DHCP [2]) from a large ISP (Internet
Service Provider)).
could log and report this information to the adversary.
Recall that we have assumed that an adversary could be aware of the
owner and the legal users of a target file. Assuming that a user
accesses only a small subset of the total number of files on the
overlay network (including the target file) the adversary can narrow
down the set of nodes on the overlay network that may potentially hold
the target file. Note that this is a worst-case-assumption; in most
cases it may not possible to associate a user with one or a small
number IP-addresses (say, when the user obtains IP-address dynamically
(DHCP [2]) from a large ISP (Internet
Service Provider)). ![]() could be
encrypted to rule out the possibility of identifying a file from its
contents. Even when the replicas are encrypted, an adversary can
exploit the fact that all the replicas of file
could be
encrypted to rule out the possibility of identifying a file from its
contents. Even when the replicas are encrypted, an adversary can
exploit the fact that all the replicas of file ![]() are
identical. When an adversary compromises a good node, it can extract a
list of identifier and file content pairs (or a hash of the file
contents) stored at that node. Note that an adversary could perform a
frequency inference attack on the replicas stored at malicious nodes
and infer their filenames. Hence, if an adversary were to obtain the
encrypted contents of one of the replicas of a target file
are
identical. When an adversary compromises a good node, it can extract a
list of identifier and file content pairs (or a hash of the file
contents) stored at that node. Note that an adversary could perform a
frequency inference attack on the replicas stored at malicious nodes
and infer their filenames. Hence, if an adversary were to obtain the
encrypted contents of one of the replicas of a target file ![]() , it could examine the extracted list of identifiers and
file contents to obtain the identities of other replicas. Once, the
adversary has the locations of
, it could examine the extracted list of identifiers and
file contents to obtain the identities of other replicas. Once, the
adversary has the locations of ![]() copies of a
file
copies of a
file ![]() , the
, the ![]() could be
attacked easily. This attack is especially more plausible on read-only
files since their contents do not change over a long period of time. On
the other hand, the update frequency on read-write files might guard
them file replica inference attack.
could be
attacked easily. This attack is especially more plausible on read-only
files since their contents do not change over a long period of time. On
the other hand, the update frequency on read-write files might guard
them file replica inference attack. ![]() would implicitly be authorized
to access the group of files to which
would implicitly be authorized
to access the group of files to which ![]() belong. However,
the later scenario may seriously impede the system's performance in
situations where it may require location key to be changed each time
the group membership changes.
belong. However,
the later scenario may seriously impede the system's performance in
situations where it may require location key to be changed each time
the group membership changes. ![\includegraphics[width=\linewidth]{fig/pr-dos.eps}](img144.png)
![\includegraphics[width=\linewidth]{fig/comp1.eps}](img145.png)
![\includegraphics[width=\linewidth]{fig/comp2.eps}](img146.png)
![]() or more of its replicas are
stored at either malicious nodes or compromised nodes. Figure 5 shows the probability of an attack
for different values of corruption threshold (
or more of its replicas are
stored at either malicious nodes or compromised nodes. Figure 5 shows the probability of an attack
for different values of corruption threshold (![]() )
and varying
)
and varying ![]() (measured in number of node
recoveries per node compromise). We ran the simulation for a duration
of
(measured in number of node
recoveries per node compromise). We ran the simulation for a duration
of ![]() time units. Recall that
time units. Recall that ![]() denotes the mean time required for one
malicious node to compromise a good node. Note that if the simulation
were run for infinite time then the probability of attack is always
one. This is because, at some point in time,
denotes the mean time required for one
malicious node to compromise a good node. Note that if the simulation
were run for infinite time then the probability of attack is always
one. This is because, at some point in time, ![]() or
more replicas of a target file would be assigned to malicious nodes (or
compromised nodes) in the system.
or
more replicas of a target file would be assigned to malicious nodes (or
compromised nodes) in the system.
![]() , the
system is highly vulnerable since the node recovery rate is lower than
the node compromise rate. Note that while a DoS attack could tolerate
powerful malicious nodes (
, the
system is highly vulnerable since the node recovery rate is lower than
the node compromise rate. Note that while a DoS attack could tolerate
powerful malicious nodes (
![]() ), the host compromise attack cannot tolerate the
situation where the node compromise rate is higher than their recovery
rate (
), the host compromise attack cannot tolerate the
situation where the node compromise rate is higher than their recovery
rate (
![]() ). This is primarily because of the cascading
effect of host compromise attack. The larger the number of compromised
nodes we have, the higher is the rate at which other good nodes are
compromised (see the adversary model in Section 3). Table 2 shows the mean fraction of good
nodes (
). This is primarily because of the cascading
effect of host compromise attack. The larger the number of compromised
nodes we have, the higher is the rate at which other good nodes are
compromised (see the adversary model in Section 3). Table 2 shows the mean fraction of good
nodes (![]() ) that are in an uncompromised state
for different values of
) that are in an uncompromised state
for different values of ![]() . Observe from Table 2 that when
. Observe from Table 2 that when ![]() , most of the good nodes are in compromised state.
, most of the good nodes are in compromised state. ![]() ). The
effort required is expressed in terms of the fraction of good that need
to be compromised by the adversary to attack the target file.
). The
effort required is expressed in terms of the fraction of good that need
to be compromised by the adversary to attack the target file. ![]() good nodes in order to succeed a
targeted file attack. Clearly, location key based techniques increase
the required effort by several orders of magnitude. For instance, when
good nodes in order to succeed a
targeted file attack. Clearly, location key based techniques increase
the required effort by several orders of magnitude. For instance, when ![]() , an adversary has to compromise 70% of the good
nodes in the system in order to attain the probability of an attack to
a nominal value of
, an adversary has to compromise 70% of the good
nodes in the system in order to attain the probability of an attack to
a nominal value of ![]() , even under the assumption
that an adversary collects file capabilities from compromised nodes. If
an adversary compromises every good node in the system once, it gets to
know the tokens of all files stored on the overlay network. In Section 7.3 we had proposed location re-keying
to protect the file system from such attacks. The exact period of
location re-keying can be derived from Figure 6. For instance, when
, even under the assumption
that an adversary collects file capabilities from compromised nodes. If
an adversary compromises every good node in the system once, it gets to
know the tokens of all files stored on the overlay network. In Section 7.3 we had proposed location re-keying
to protect the file system from such attacks. The exact period of
location re-keying can be derived from Figure 6. For instance, when ![]() , if a user wants to retain the attack probability
below 0.1, the time interval between re-keying should equal the amount
of time it takes for an adversary to compromise 70% of the good nodes
in the system. Table 3 shows the
time taken (normalized by
, if a user wants to retain the attack probability
below 0.1, the time interval between re-keying should equal the amount
of time it takes for an adversary to compromise 70% of the good nodes
in the system. Table 3 shows the
time taken (normalized by ![]() ) for an adversary to increase the attack
probability on a target file to 0.1 for different values of
) for an adversary to increase the attack
probability on a target file to 0.1 for different values of ![]() . Observe that as
. Observe that as ![]() increases,
location re-keying can be more and more infrequent.
increases,
location re-keying can be more and more infrequent.