Check out the new USENIX Web site. next_inactive up previous


Fixing Races for Fun and Profit: How to abuse atime

Nikita Borisov Rob Johnson Naveen Sastry David Wagner
University of California, Berkeley
{nikitab, rtjohnso, nks, daw}@cs.berkeley.edu

Abstract:

Dean and Hu proposed a probabilistic countermeasure to the classic access(2)/open(2) TOCTTOU race condition in privileged Unix programs [4]. In this paper, we describe an attack that succeeds with very high probability against their countermeasure. We then consider a stronger randomized variant of their defense and show that it, too, is broken. We conclude that access(2) must never be used in privileged Unix programs. The tools we develop can be used to attack other filesystem races, underscoring the importance of avoiding such races in secure software.


Introduction

At USENIX Security 2004, Dean and Hu described a probabilistic scheme for safely using the access(2) system call in Unix systems [4]. The access(2) system call is known to be vulnerable to Time Of Check To Time Of Use (TOCTTOU) race attacks, and for this reason it has fallen into almost complete disuse. This leaves Unix programmers without a portable, secure, and efficient way of checking a file's permissions before opening it. Thus Dean and Hu's scheme would be a boon to systems programmers if it were secure. In this paper, we show that it is not.

Dean and Hu's scheme, which we call $ k$-Race, thwarts attackers by forcing them to win numerous races to successfully attack the system. The strength of their scheme rests on the assumption that an attacker has a low probability of winning each race, and hence an exponentially low probability of winning all the races. Dean and Hu identify two difficulties with winning repeated races: ensuring that the attacker gets scheduled in time to win each race, and staying synchronized with the victim over many successive races. We develop three tools which help us overcome these difficulties: filesystem mazes, which greatly slow down filesystem operations of a victim, system call synchronizers, and system call distinguishers. Using these tools, we can win races with extremely high probability, violating Dean and Hu 's assumption. We use these tools to build an attack that reliably breaks the $ k$-Race algorithm using the recommended parameter, and works on a variety of operating systems. As shown in Table 1, our attack defeats the $ k$-Race algorithm over 90% of the time on every operating system we tested.


Table 1: Success rates of our attack against Dean and Hu's defense using the recommended security parameter, $ k=7$, on several platforms.
OS Attacker Wins / Trials
FreeBSD 4.10-PR2 $ 92/100$
Linux 2.6.8 $ 98/100$
Solaris 9 $ 100/100$


Our attack remains successful even when the security parameter is much larger than recommended by Dean and Hu. We also consider a randomized extension of the $ k$-Race algorithm that makes non-deterministic sequences of calls to access(2), open(2), and fstat(2), and show that it can be defeated as well. The tools we develop for this attack are applicable to other Unix filesystem race vulnerabilities, such as the stat(2)/open(2) race common in insecure temporary file creation. We have ported our attack code to several Unix variants and it succeeds on all of them. Our technique exploits the performance disparity between disks and CPUs, so as this gap grows our attack will become more powerful. This refutes Dean and Hu 's claim that as CPU speeds increase in the future, the risk to systems using their defense would decline.

Recent research in automated code auditing has discovered over $ 40$ TOCTTOU races in the Red Hat Linux distribution [10]. This result, combined with our techniques for exploiting race conditions, shows that races are a prevalent and serious threat to system security.

In short, we show that the $ k$-Race algorithm is insecure, that Unix filesystem races are easy to win, and that they will continue to be easy to win for the foreseeable future. The rest of this paper is organized as follows. We begin by reviewing setuid programs in Unix and the access(2)/open(2) race. Section 3 presents Dean and Hu 's countermeasure for preventing access(2)/open(2) races. We then describe a simple attack on Dean and Hu 's scheme in Section 4, and enhance this attack in Section 5. Sections 6 and 7 describe a randomized generalization of the $ k$-Race algorithm, and an attack on that scheme. Section 8 considers other defenses against the access(2)/open(2) race. We consider related work in Section 9, and summarize our contributions in Section 10.

The access(2)/open(2) race

The access(2) system call was introduced to address a problem with setuid-root programs. The original Unix authors invented the setuid mechanism to support controlled sharing in Unix environments. A setuid program runs with the permissions of the executable's owner instead of the invoker, enabling it to use private data files that the program's invoker cannot access. As a special case, a setuid-root program can access any file on the system, including the invoker's personal files. This leads to a classic confused deputy problem [6].

To see how the confused deputy problem arises, consider a setuid-root printing program that prepares users' files for printing and puts them onto the printing queue.1The queue is not accessible to ordinary users, but the setuid-root program can write to it. The program should only let users print files that they themselves can access. Unfortunately, since setuid-root programs have permission to read every file on the system, this implementation does not have any easy way to determine whether the requested input file is readable by the caller.

To solve this problem, Unix introduced the access(2) system call. A setuid program can use the access(2) system call to determine whether the invoker has the rights needed to open a file. This solves the confused deputy problem, but it also introduces a new security vulnerability: Time Of Check To Time Of Use races [8]. The vulnerability occurs because the return value from access(2) tells us about the state of the filesystem at some recent time in the past, but tells us nothing about what the state will be when we next operate on the filesystem.

To illustrate the vulnerability, consider a typical setuid program, which might call access(2) to check a file's permissions and then call open(2) to actually open the file if the check succeeds, as shown in Figure 1. Unfortunately, this code idiom is insecure. A clever attacker can attempt to modify the filesystem (e.g. by changing symbolic links) between the access(2) and open(2) system calls so that when the setuid program calls access(2), the given filename points to a safe, accessible file, but when the setuid program calls open(2), the filename points to a protected file. Thus, even if a setuid program uses access(2), an attacker can still trick it into opening files that it should not.

Figure 1: A setuid-root program vulnerable to the access(2)/open(2) TOCTTOU race attack. An attacker may be able to change the filesystem between the calls to access(2) and open(2).
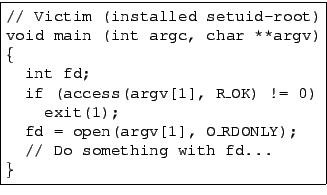\fbox{\begin{minipage}{3in} {\ttfamily \begin{tabbing} // Victim (installed setu... ...\_RDONLY);\\ \>// Do something with fd...\\ \} \end{tabbing}} \end{minipage}}

Figure 2: A program for exploiting access(2)/open(2) races. A non-root attacker can use this program to exploit the setuid-root program shown in Figure 1.
\fbox{\begin{minipage}{3in} {\ttfamily \begin{tabbing} // Attacker \\ vo\=id ma... ...');\\ \>symlink(''dir1'', ''activedir'');\\ \} \end{tabbing}} \end{minipage}}

Figure 1 shows a typical setuid-root program that is vulnerable to the access(2)/open(2) race, and Figure 2 shows a simple attack program that can trick the victim into opening /etc/shadow, a file that only root can read. The attack is very timing dependent: the attack program only succeeds if it manages to interrupt the victim program between its access(2) call and open(2) call. When this happens, the access(2) call succeeds because, at that time, the path activedir/lnk resolves to a user-accessible file, public_file. After the victim calls access(2), it gets interrupted, and the victim changes the symbolic link activedir to point to dir1. When the victim resumes, it calls open(2) on activedir/lnk, which now resolves to /etc/shadow. Since the victim is a setuid-root program, the open(2) succeeds, but the victim believes that it has opened a file accessible by the invoking user.

Notice that the attacker has a much better chance of winning the race if dir0 is not currently in the buffer cache. If that is the case, then the victim's call to access(2) will have to fetch the contents of dir0 from disk. This I/O will put the victim to sleep, giving the attacker a chance to run and switch the symbolic link activedir. This observation is one of the key ideas behind our attack on the $ k$-Race defense.


The $ k$-Race proposal

Figure 3: Dean and Hu's $ k$-Race algorithm [4]. An attacker must win $ 2k+1$ races to defeat this algorithm.
\begin{figure}\verbatiminput{dean-code}\end{figure}

Dean and Hu noticed that, in practice, exploiting the access(2) race condition can be quite difficult. Their experiments showed that a naive attacker can only expect to win a race with probability $ 10^{-3}$ on uniprocessor machines and $ 10^{-1}$ on multiprocessor machines. Based on this evidence, Dean and Hu proposed a probabilistic countermeasure to this race condition. By requiring the attacker to win a large number of races, they intended to make it practically impossible to successfully exploit the access(2)/open(2) race.

An implementation of their defense is given in Figure 3. The $ k$-Race algorithm essentially repeats the access(2)/open(2) idiom $ k$ times. To ensure that the attacker must win a race between every system call, the $ k$-Race algorithm uses fstat(2) to check that every open(2) call resolves to the same file. To see how this works, consider an attacker trying to defeat $ k$-Race. After the victim makes the first access(2) call, the attacker must switch symlinks so that, when the victim calls open(2), the given filename points to a protected file. After the first call to open(2), the attacker has tricked the victim into opening a secret file, but the $ k$-Race algorithm forces the attacker to continue racing with the victim as follows. The victim next performs another call to access(2). The attacker must race to switch the symlink to point to a public file, or this access(2) call will not succeed. Next, the victim calls open(2) again and uses fstat(2) to verify that the resulting file descriptor is a handle on the same file as the result of the first call to open(2). In order for this test to succeed, the attacker must race to switch the symlinks again to point to the private file. By making four system calls, access(2), open(2), access(2), open(2), the victim has forced the attacker to win three races.

In general, the $ k$-Race algorithm allows the setuid-root program to make $ k$ strengthening rounds of additional calls to access(2) and open(2), forcing the attacker to win a total of $ 2k+1$ races. Dean and Hu reason that, since the adversary must win all $ 2k+1$ races, the security guarantees scale exponentially with the number of rounds. If $ p$ is the probability of winning one race, then the attacker will defeat the $ k$-Race defense with probability $ \approx p^{2k+1}$. Their measurements indicate that $ p \le 1.4 \times 10^{-3}$ on uniprocessor machines on a range of operating systems, and $ p \le 0.12$ on a multiprocessor Sun Solaris machine. Dean and Hu suggest $ k=7$ as one reasonable parameter setting, and they estimate that with this choice the probability of a successful attack should be below $ 10^{-15}$.

In their argument for the security of their scheme, Dean and Hu consider a slightly modified attacker that attempts to switch activedir back and forth between dir0 and dir1 between each system call made by the victim. They observe that this attack will fail for two reasons. First, the attacker is extremely unlikely to win any race if dir0 is in the filesystem cache. Moreover, even if the attacker gets lucky and dir0 is out of cache during the victim's first call to open(2), the victim's call to open(2) will bring dir0 into the cache. In this case, dir0 will be in the cache for the victim's second call to open(2), so the attacker will lose that race. Dean and Hu 's experiments support this claim. Second, they note that this attack requires that the attacker remain synchronized with the victim. Dean and Hu added random delays between each access(2) and open(2) call to foil any attempts by the attacker to synchronize with the victim.

Although filesystem caching and synchronization are real problems for an attacker, we show in the next section that it is possible to modify the attack to overcome these difficulties.


Basic Attack

As Dean and Hu observed, an attacker must overcome two obstacles to successfully attack their scheme. First, filesystem caching prevents the attacker from winning multiple races. Second, the attacker must synchronize with the victim. We deal with each problem in turn.

Avoiding the cache.

The attack analyzed by Dean and Hu succumbs to caching effects because it re-uses dir0 and dir1. To avoid filesystem caching, we create $ 16$ separate directories, dir0, $ \ldots $, dir15, and use each directory exactly once. The even-numbered directories dir0, dir2, $ \ldots $, dir14 all contain symbolic links to a publicly accessible file. The odd-numbered directories, dir1, dir3, $ \ldots $, dir15, contain symbolic links to the protected file we are attacking, such as /etc/shadow. Initially, the symbolic link activedir points to dir0. After each of the victim's system calls, the attacker changes activedir to point to the next directory, as shown in the pseudo-code in Figure 4.

Figure 4: Our algorithm for defeating the $ k$-Race algorithm. The algorithm forces the victim to perform I/O, and hence yield the CPU to the attacker, by switching among a series of directories, dir0, $ \ldots $, dir15, all of which are out of the filesystem cache. The attacker detects the start of each of the victim's system calls by monitoring the access time of symbolic links in each directory.
\fbox{\begin{minipage}{3in} \begin{tabbing} \= {\bf for} \= $i = 1 $ {\bf to} ... ...\> {\bf link} {\tt activedir} {\bf to} {\tt dir}$i$\end{tabbing}\end{minipage}}

Since the attacker uses each directory exactly once, she has a much higher chance of winning all the races against the victim. If the attack begins with none of the directories in cache, then the victim will be forced to sleep on I/O for each of its system calls, giving the attacker time to update activedir to point to the next directory.

This attack succeeds only when dir0, $ \ldots $, dir15 are not in the operating system's buffer cache. If the attacker tries to run the attack immediately after creating these directories, she will fail because they will all still be in the cache. For the rest of this section, we assume the attacker has some method to flush all these directories from cache after creating them. Section 5 describes a more powerful attack that eliminates this assumption.

Staying in sync.

To stay synchronized with the victim, the attacker must be able to detect when the victim has begun each call to access(2) or open(2). The key insight is that Unix updates the access time on any symbolic links it traverses during name resolution.2The attacker can use this to monitor the filesystem operations performed by the victim. The attacker simply needs to poll the access time of a symbolic link in the path it passes to the victim. When the access time of that link changes, the victim must have begun a call to access(2) or open(2).

Unfortunately, there is a small hitch with this simple approach. In Unix, the access time is recorded only to a $ 1$-second granularity. Consequently, the attacker cannot poll the access time of activedir because, every time she updates activedir to point to a new directory, she will change its access time to the current second, and hence will not be able to detect further accesses for up to a second. By then, the race will be over. Moreover, the attacker cannot poll the access time on dir7/lnk since this would pull dir7 into the filesystem cache. This makes it a challenge to stay synchronized with the victim.

This hurdle can be surmounted with an appropriate re-arrangement of the directory structure. See Figure 5 for the directory structure we use to enable polling without disturbing the filesystem cache. Inside each directory, diri, we create another subdirectory iotrap and a symbolic link sentry pointing to iotrap. We then create the final link, lnk, that points to the public or protected file inside diri/iotrap. The attacker gives the victim the filename activedir/sentry/lnk, and polls the access time of activedir/sentry.

Figure 5: The directory structure used in our basic attack on the $ k$-Race algorithm. The attacker synchronizes with the victim by polling the access time of diri/sentry. The attacker must first flush all the iotrap directories from the filesystem cache so that the victim will sleep on I/O when it traverses them. The attacker creates a symbolic link activedir pointing to dir0 and runs the victim with arguement activedir/sentry/lnk.
\fbox{\begin{minipage}{3in} \begin{tabbing} {\tt dir0/iotrap/lnk} \= $ \xright... ...rrow{\mathrm{symlink}} $\xspace {\tt dir15/iotrap} \end{tabbing}\end{minipage}}

Summary.

  1. The attacker creates $ 16$ directories as shown in Figure 5 and a symbolic link activedir to dir0.
  2. She forces the cache entries for these directories out of memory.
  3. The attacker then executes the victim with argument activedir/sentry/lnk.
    1. The victim calls access(2). The kernel begins traversing this path and updates the access time on dir0/sentry. After resolving the symbolic link dir0/sentry, the victim is put to sleep while the operating system loads the contents of dir0/iotrap. The victim is now suspended in the middle of executing the access(2) call.
    2. The attacker then gains the CPU, and polls the access time on dir0/sentry. Upon noticing that the access time has been updated, the attacker knows that the victim has begun its first access(2) call. The attacker switches activedir to point to dir1 and begins polling the access time on dir1/sentry. The victim's suspended access(2) call will not be affected by this change to activedir because it has already traversed that part of the path.
    3. Eventually, the victim's I/O completes and it finishes the access(2) call successfully.
When the victim calls open(2), the exact same sequence of events occurs: the kernel updates the access time on dir1/sentry, the victim sleeps on I/O loading dir1/iotrap, the attacker runs and notices the updated access time on dir1/sentry, the attacker switches activedir to point to dir2, and the victim completes the open(2) successfully. This process repeats for the victim's remaining system calls, and the attacker fools the victim into opening a protected file.

We implemented and tested this simple attack on several different machines and found that the attack works but is extremely sensitive to the target machine's state. For example, if the directories used in the attack happen to be arranged close together on disk, then the attack will often fail. In the next section, we develop a robust version of this attack that succeeds with high probability on all the machines we tested.


Full Attack

In this section, we increase the power and reliability of our attack. The full attack is robust, succeeds with high probability, can defeat the $ k$-Race algorithm with over $ 100$ rounds of strengthening, and doesn't depend on the attacker's ability to perfectly flush the kernel filesystem cache.

I/O amplification.

We develop a tool called a maze to slow down the I/O operations of the victim and hence increase the chances that it will sleep. We start by creating a deep tree of nested directories. For example, inside dir0, the attacker creates the tree dir/dir/.../dir/lnk instead of just dir/lnk. We call such a deep nested directory structure a chain. The link sentry should now point to dir/dir/.../dir, and hence the attacker still runs the victim with the argument activedir/sentry/lnk. The victim will be forced to sleep on I/O if at least one of the directories in the chain is not currently in the buffer cache. Most Unix systems impose a limit on the length of filename paths, known as MAXPATHLEN, and this limits the depth of chains created by the attacker. Common values for MAXPATHLEN are $ 1024$ and $ 4096$ characters. Even with these limits an attacker can create a directory tree over $ 500$ directories deep, but the attacker can do even more.

Figure 6: Malicious directory structure to force the victim to sleep on I/O with extremely high probability and hence enable the attacker to win a single race. We call this structure a maze. We place an arrow between a symbolic link and the target it references in a dotted box.
\includegraphics[width=3.25in]{maze}

Figure 7: Algorithm to create the directory structure in Figure 6.
\fbox{\begin{minipage}{3in} \begin{tabbing} {\bf procedure} {\bf make\_maze}({... ... \> {\bf link} {\tt sentry} {\bf to} {\it target} \end{tabbing}\end{minipage}}

MAXPATHLEN only limits the number of path elements that may be specified in a single system call, it does not limit the number of directory elements that may be traversed during a single name lookup. An attacker can use symbolic links to connect two chains together as follows. First, the attacker creates a chain chain0/dir/dir/.../dir/lnk, as above. Then she creates another chain chain1/dir/dir/.../dir/lnk, where the symbolic link at the bottom of this chain points to chain0/dir/dir/.../dir. The sentry link should now point to chain1/dir/dir/.../dir. Now the attacker can invoke the victim, passing it the path activedir/sentry/lnk/lnk. If each chain is $ N$ directories deep, then the victim will need to traverse $ 2N$ directories to resolve this filename.

This technique can be extended to create a maze of up to $ C$ chains, chain$ C-1$, chain$ C-2$, ..., chain0, where each chain has at its bottom a symbolic link pointing to the bottom of the next chain. Figure 6 shows one such maze of directories in its entirety. For simplicity, we create a final link, exit, pointing to the target file, at then end of the maze. We also use shorter names for the directories in each chain, enabling us to create deeper chains within the constraints of MAXPATHLEN. Pseudocode for constructing this maze is given in Figure 7. With this structure, the attacker runs the victim with the filename argument activedir/sentry/lnk/.../lnk/lnk.


Table 2: MAXPATHLEN, the symbolic link limit, and other relevant parameters for three common Unix variants. Notice that on Linux a single filename lookup can require traversing over $ 300$MB of on-disk data.
OS Filesystem MAXPATHLEN Link limit Dir. Size Max. Maze Max. Maze
        (KB) Length Size (MB)
Linux 2.6.8 ext3 $ 4096$ 40 $ 4$ $ 81920$ $ 327$
Solaris 9 ufs $ 1024$ 20 $ 0.5$ $ 10240$ $ 5$
FreeBSD 4.10-PR2 ufs $ 1024$ 32 $ 0.5$ $ 16384$ $ 8$


With $ C$ chains, each $ N$ directories deep, the victim will have to traverse $ CN$ directories to resolve the given filename. Unix systems usually impose a limit on the total number of symbolic links that a single filename lookup can traverse. Table 2 gives the MAXPATHLEN and link limit for some common versions of Unix. For example, Linux 2.6 limits filename lookups to 40 symbolic links to prevent ``arbitrarily long lookups.''3 This limits the attacker to $ C<40$. Despite this limit, the attacker can still force the victim to visit over $ 80,000$ directories every time it calls access(2) or open(2). The attacker is very likely to win the race if even just one of these directories is not in the filesystem buffer cache.

Table 2 also shows the on-disk size of the largest maze possible on each system. This figure gives us some insight into why this attack is so successful. For example, under Linux 2.6, an attacker can construct a filename that requires loading over 300MB of data from disk, just to resolve it. It is not surprising that when the victim calls access(2) or open(2) on such a filename it is extremely likely to sleep on I/O, giving the attacker plenty of time to execute her attack.

Probabilistic cache flushing.

Mazes are so powerful that the attacker does not need to flush all the attack directories from cache. Instead, she can simply do ``best effort'' flushing by engaging in filesystem activity of her own. This activity will cause the buffer cache to flush old items to make space for the new ones. For example, running the command grep -r any_string /usr > /dev/null 2>&14 populates the buffer cache with new items and will often flush some of the attack directories from the cache. With large mazes, the recursive grep is very likely to flush at least one of the directories in each maze, enabling the attacker to successfully break the $ k$-Race algorithm.

Figure 8: Malicious directory structure to attack the $ k$-Race defense using the maze structure from Figure 6. This construction is particularly effective when $ k$ is large.
\includegraphics[width=2in]{entirestructure-notarget}

Summary.

To defeat $ k$-Race using $ k$ strengthening rounds, the attacker creates $ M=2k+2$ directories, maze0, $ \ldots $, maze$ 2k+1$, builds a maze in each of these directories, and sets the symlink activemaze to initially point to maze0, as shown in Figure 8. The exit links in the even-numbered mazes point to an attacker accessible file, and the exit links in the odd-numbered mazes point to the protected file under attack. After creating this directory setup, the attacker uses grep or some other common Unix tool to flush some of the directories in the mazes out of cache. She then executes the victim with the path activemaze/sentry/lnk/.../lnk and advances activemaze to point to the next maze directory whenever she detects that the access time of activemaze/sentry has changed.

Experimental results.

We implemented the $ k$-Race algorithm, including randomized delays between every system call and between each round of strengthening. We did not implement the extended $ k$-Race defenses, such as setting the victim scheduling priority to FIFO or using mlock() to pin its pages in memory. We do not believe these enhancements would prevent our attack from succeeding.


Table 3: Attack success rates against the $ k$-Race algorithm. $ k$ is the $ k$-Race security parameter, $ M$ is the number of maze directories used for the attack, $ C\times N$ is the total number of directories in each maze. We used grep to flush the filesystem cache before each trial. The first three experiments show that our maze attack works on several versions of Unix and scales to large values of $ k$ by using more mazes. The three experiments against the randomized $ k$-Race algorithm show that our system call distinguishers are effective, and that our attack is insensitive to the ordering of the victim's calls to access(2), open(2), and fstat(2). The last experiment with $ k=1000$ shows that by re-using mazes we can even attack extremely large values of $ k$.
OS $ k$-Race Parameters Attack Parameters Wins / Trials
  $ k$ Randomized $ M$ $ C\times N$  
Linux 2.6.8 $ 100$ No $ 201$ $ 400$ $ 22/100$
Solaris 9 $ 100$ No $ 201$ $ 400$ $ 83/100$
FreeBSD 4.10-PR2 $ 100$ No $ 201$ $ 200$ $ 100/100$
Linux 2.6.8 $ 100$ Yes $ 201$ $ 400$ $ 19/100$
Solaris 9 $ 100$ Yes $ 201$ $ 1200$ $ 77/100$
FreeBSD 4.10-PR2 $ 100$ Yes $ 201$ $ 200$ $ 88/100$
Linux 2.6.8 $ 1000$ No $ 50$ $ 7000$ $ 83/100$


We implemented and tested the attack on three Unix variants: Linux 2.6.8, Solaris 9, and FreeBSD 4.10-PR2. The Linux machine contains a $ 1.3$GHz AMD Athlon processor, $ 1$GB of RAM,and a $ 160$GB, $ 7200$RPM IDE disk with an $ 8$MB on-disk cache and $ 9$ms average seek time. The FreeBSD machine contains a $ 1.4$GHz Pentium IV, $ 512$MB of RAM, and a $ 40$GB, $ 7200$RPM IDE disk with a $ 2$MB on-disk cache and $ 8.5$ms average seek time. The Solaris machine is a multiprocessor with two $ 450$MHz UltraSPARC processors, $ 1$GB of RAM, and a RAID-1 mirror built on two $ 9$GB SCSI disks: one $ 10,000$RPM drive with a $ 4$MB buffer, and one $ 7200$RPM disk with a $ 2$MB buffer. The Linux machine used the ext3 filesystem, while the Solaris and FreeBSD machine each used ufs. Table 2 summarizes the configuration and capabilities of each machine and its operating system. Our results are given in Table 3, and show that, even with $ k=100$, we can defeat the $ k$-Race algorithm easily on a variety of systems. For example, we were able to win $ 83$ out of $ 100$ trials on Solaris, and $ 100$ out of $ 100$ trials on FreeBSD.

We stop short of performing an exhaustive analysis of how individual factors such as memory size, hard drive model, and operating system affect the success of our attack. Our goal is simply to show that the attack is successful under a broad sampling of realistic hardware and software characteristics, which is sufficient evidence that the $ k$-Race defense must not be used in practice.

Extensions.

Our attack avoids the filesystem cache by using a separate maze for each of the victim's system calls, but we can re-use mazes for extremely large values of $ k$. As shown in Table 2, large mazes can consume over $ 300$MB of disk space on some operating systems. A machine with, say, $ 1$GB of RAM can only cache $ 3$ of these mazes, so after the victim performs $ 4$ system calls, the operating system will have flushed many of the cache entries for directories in the first maze. The attacker can therefore safely reuse the first maze. In general, the adversary can break the $ k$-Race defense using extremely large $ k$ by creating as many mazes as necessary to fill the filesystem cache and then cycling among these mazes during the attack. We used this technique to attack $ k$-Race with $ k=1000$ on Linux 2.6, and found that with 50 mazes of sizes 28MB each, we can break the $ k$-Race defense 83 times out of 100. (We used mazes smaller than the maximal size because, even with this size of maze, a single trial was taking over 5 minutes.)

If the I/O amplification methods described above are not sufficient to enable the attacker to win races handily, she can create thousands of dummy files in each directory of each chain. This method of slowing down name resolution was previously suggested by Mazières and Kaashoek [5]. These dummy entries will force the kernel to read even more data from disk while performing name resolution for each of the victim's system calls. As mentioned above, resolving a filename through a maze may require reading hundreds of megabytes of data from disk. By adding dummy entries in each chain directory, an attacker can force the kernel to read gigabytes of data from disk. We did not implement this extension because the basic mazes were sufficient to attack every system we tested.

In summary, we have shown a practical attack against the $ k$-Race defense using extremely high values for the security parameter $ k$ and on a variety of Unix operating systems.


A Randomized $ k$-Race Algorithm

Dean and Hu 's defense performs a deterministic sequence of access(2) and open(2) system calls, and the attack in Section 4 exploits that by deterministically switching between a publicly accessible file and the target file. This suggests a potential countermeasure to our attack: in each iteration of strengthening, the victim randomly chooses to perform either an access(2) or open(2) call. Now our attack will fail unless it can determine the victim's sequence of system calls. We next introduce system call distinguishers to overcome this obstacle.


Attack on Randomized $ k$-Race

Recall that our attack program gains access to the CPU while the victim is in the middle of executing one of its system calls, so it is impossible for the adversary to predict the victim's next system call. Instead, we describe methods for determining the victim's current system call and reacting appropriately.

Figure 9: Malicious directory structure for attacking the randomized $ k$-Race defense. The exit links in each maze point to the symbolic link target and the attacker points target to the public or protected file depending on the victim's current system call.
\includegraphics[width=2in]{entirestructure}

Distinguishing access(2) and open(2) calls is surprisingly easy on most Unix operating systems. In Solaris 9, any process can read the current system call number of any other process from /proc/pid/psinfo. Linux and FreeBSD do not export the system call numbers of processes, but we can exploit a side effect of their implementations of the access(2) system call. Recall that access(2) enables a setuid-root process to determine if the invoking user can access a certain file. When a setuid-root process runs, the invoking user's ID is stored in the processes real user ID, and its effective user ID is set to 0, giving it root privileges. FreeBSD implements the access(2) system call by copying the process's real user ID to its effective user ID, resolving the given filename and performing permission checks using the effective user ID, and then restoring the effective user ID to its original value. Every process's real and effective user IDs can be read from /proc/pid/status on FreeBSD, so an attacker can determine whether the victim is currently calling access(2) or open(2) by simply checking the victim's user IDs: if the victim's effective and real user IDs are equal, then it is calling access(2), otherwise it is calling open(2). Linux implements access(2) in a similar way, but Linux has a notion of a process ``filesystem user ID'' (fsuid) that is used in all filesystem-related permission checks. The Linux access(2) system call copies the process's real user ID to its filesystem user ID instead of its effective user ID, but the attacker can still use the same idea. She simply checks whether the victim's filesystem ID is equal to its real user ID. We have tested these access(2)/open(2) distinguishers on Solaris 9, Linux 2.6, and FreeBSD, and they all work. Based on our reading of OpenBSD's source code, its access(2) implementation behaves just like FreeBSD's, so this attack should work on OpenBSD, as well.

Figure 10: Attacker's algorithm to defeat the $ k$-Race scheme after setting up the directory structure depicted in Figure 9. The victim opens the file activemaze/sentry/lnk/lnk/.../lnk.
\fbox{\begin{minipage}{3in} \begin{tabbing} \= {\bf for} \= $i = 1 $ {\bf to}... ...bf link} {\tt activemaze} {\bf to} {\tt maze$i$} \end{tabbing}\end{minipage}}

Once the adversary has determined which system call the victim is executing, she must change the symbolic links in the maze to ensure the victim's system call succeeds. Toggling activemaze will not work because, by the time the attacker gets to run, the victim has already resolved that symbolic link. The attacker needs to switch a symbolic link that the victim has not processed yet. To support this operation, we set up the mazes as shown in Figure 9, and the attacker toggles the symbolic link, target, between the public and protected files based on the victim's current system call. Figure 10 shows the attacker's new algorithm. When the victim makes a system call, it is forced to sleep on I/O while resolving the filename. The attacker then wakes up, determines the victim's current system call, switches target so the victim's system call will succeed, and advances activemaze to point to the next maze. When the victim resumes, it finishes resolving the filename using the new value for target, so the system call succeeds.


Table 4: Running times for different access(2)/open(2) techniques on different operating systems. We measured the elapsed cycle count for each call and repeated each measurement 1000 times to compute the average speed. The measurements for the $ k$-Race algorithm do not include randomized waits, so these results are a lower bound on the running time of $ k$-Race.
  Linux 2.6 FreeBSD 4.10-PR2 Solaris 9
  1.7 GHz Athlon 1.3GHZ P-IV 450MHZ Ultra
access(2)/open(2) 3 $ \mu$ sec 8 $ \mu$ sec 253 $ \mu$ sec
$ k$-Race, $ k=7$ 30 $ \mu$ sec 91 $ \mu$ sec 2210 $ \mu$ sec
$ k$-Race, $ k=100$ 393 $ \mu$ sec 1190 $ \mu$ sec 27600 $ \mu$ sec
Fork-Open 135 $ \mu$ sec 582 $ \mu$ sec 5750 $ \mu$ sec


We tested this attack on Linux, Solaris, and FreeBSD. Table 3 shows our results. Against the randomized $ k$-Race algorithm using $ k=100$ our attack won at least 19% of the trials and up to 88%. From this, we conclude that the randomized $ k$-Race algorithm is not secure. Note also that by using system call distinguishers our attack on the randomized algorithm performs about as well as the attack on the deterministic algorithm.

The three techniques we have developed in this paper -- mazes, synchronization primitives, and system call distinguishers -- are general tools that adversaries can use to exploit a variety of Unix filesystem races. For this reason, we believe that race condition exploits are real threats that should be treated with the same level of care as other software vulnerabilities, such as buffer overflows and format string bugs.


Other Defenses

Fork.

As mentioned by Dean and Hu , there is at least one secure, cross-platform option to solve this problem. A program can eschew the use of the access(2) system call and rely on the operating system to enforce the permission checks when it opens the file. When the program needs to open an invoker-accessible file, it can fork a new process that then uses the setuid(2) call to drop the setuid privilege and run only with the rights of the invoker. The new process can then call open(2) and the operating system will enforce that the program's invoker has rights to open the file. Once the forked process successfully obtains a file descriptor, it can use standard Unix IPC mechanisms to pass the file descriptor back to its parent process. The parent process can use the file descriptor as normal.

We have implemented this forking technique and tested it on Linux 2.4, 2.6, Solaris 9.1, and FreeBSD 4.10-PR2 [11]. Our fork(2)/open(2) function has the same interface as open(2), taking a string pathname and a flags parameter. It returns a file descriptor but ensures that the program's invoker (determined by getuid(2)) can access the file. We envision that the code can be placed in a library, such as libc.

One drawback with this technique is that it is much slower than the $ k$-Race scheme using the recommended parameter $ k=7$, as can be seen in Table 4. However, we have shown that $ k$-Race is insecure even up to $ k=100$, and our experiments show that the fork(2)/open(2) solution is faster than $ k$-Race with $ k=100$.

Kernel solutions.

Forking a process to open a file is a heavy-weight solution, and a little help from the kernel could go a long way. For example, if temporarily dropping privileges were portable across different versions of Unix, then a setuid-root program could simply temporarily drop privileges, open the file, and restore privileges. Privilege management in Unix is a notorious mess [2], but any progress on that problem would translate into immediate improvements here. Alternatively, OS kernels can add a new flag, O_RUID, to the set of flags for the open call, as suggested by Dean and Hu .

Until privilege management or the O_RUID flag become standardized, the C library can emulate these features to create a simple portable interface. For example, the C library could introduce a new set of user id management interfaces that hide all the non-portable details of each OS implementation. Similarly, the C library could emulate O_RUID by temporarily dropping privileges while performing the open(2) call.

Any solution like these would enable setuid-root programs to open files with the same security guarantees as the fork(2)/open(2) solution, but with the performance of a simple call to open(2). This would be a significant performance benefit, as shown in Table 4, and would be clearly superior to Dean and Hu 's defense in both security and speed.


Related Work

A number of projects use static analysis techniques to find race conditions in C source code. Bishop and Dilger gave one of the earliest formal descriptions of the access(2)/open(2) race condition and used this formalism to characterize when the race condition occurs [1]. Using this characterization, they developed a static analysis tool that finds TOCTTOU races by looking for sequences of file system operations that use lexically identical arguments. Because their tool performs no data flow analysis, it may fail to report some real vulnerabilities. Chen et al. used software model checking to check temporal safety properties in eight common Unix applications [3]. Their tool, MOPS, is able to detect stat(2)/open(2) races. Later work with MOPS by Schwarz et al. checked all of Red Hat 9 and found 41 filesystem TOCTTOU bugs [10]. MOPS has similar limitations to Bishop and Dilger's tool because it also doesn't perform data flow analysis.

Static analysis techniques may generate many false positives, requiring the developer to sift through numerous warnings to find the actual bugs. Dynamic techniques aim to reduce the number of false positives by observing runtime program behavior and looking for TOCTTOU race conditions. Tsyrklevich and Yee detected races by looking for ``pseudo-transactions'', i.e. pairs of system calls that are prone to TOCTTOU file race vulnerabilities [12]. Upon detecting a race in a running system, their tool asks the user for a course of action. Ko and Redmond used a similar approach to look for dangerous sequences of system calls [7]. They wrote a kernel extension that looks for interfering system calls, i.e. system calls that changes the outcome of another group of system calls. For example, their scheme would detect our attack because the attacker's unlink(2) calls interfere with the victim's calls to open(2) and access(2). Cowan et al developed RaceGuard, a kernel enhancement that prevents temporary file creation race conditions by detecting changes to the file system between calls to stat(2) and open(2). Related to Tsyrklevich and Yee's pseudo-transaction notion, the QuickSilver operating system adds support for filesystem transactions [9]. A process could prevent TOCTTOU races by enclosing dependent system calls in one transaction. Mazières and Kaashoek give principles for designing an operating system to avoid TOCTTOU bugs [5]. They note that an attacker can create many files in a directory so that name resolution slows down and hence easily win TOCTTOU file races. Their solution encompasses a richer OS interface to enable finer grain access controls and greater control over name resolution.


Conclusion

We described a practical attack on the $ k$-Race algorithm, developed a randomized version of $ k$-Race, and broke that scheme, too. The latter attack shows that our system call distinguishers are a powerful attack tool and that our attack is insensitive to the exact sequence of system calls performed by the victim. We therefore reaffirm the conventional wisdom that access(2) should never be used in secure programs. The tools we created as part of this attack -- mazes, system call synchronizers, and system call distinguishers -- are applicable to a wide variety of Unix filesystem races. We discussed several alternative solutions to access(2)/open(2) races that offer deterministic security guarantees.

Availability

The source code for our $ k$-Race implementation and attack software is available at https://nikita.ca/research/races.tar.gz.

Acknowledgements

We would like to thank David Molnar and the anonymous reviewers for their insightful comments and our shepherd, Eu-Jin Goh, for his help in preparing the final version of this paper. This work was supported in part by the NSF under grants CCR-0093337 and CCF-0430585 and by the US Postal Service.

Bibliography

1
Matt Bishop and Michael Dilger.
Checking for race conditions in file accesses.
Computing Systems, 9(2):131-152, Spring 1996.

2
Hao Chen, Drew Dean, and David Wagner.
Setuid demystified.
In Proceedings of the 11th Usenix Security Symposium, pages 171-190, August 2002.

3
Hao Chen, Drew Dean, and David Wagner.
Model checking one million lines of C code.
In Proceedings of the 11th Annual Network and Distributed System Security Symposium (NDSS), pages 171-185, February 2004.

4
Drew Dean and Alan Hu.
Fixing races for fun and profit: How to use access(2).
In Proceedings of 13th Usenix Security Symposium, pages 195 - 206, August 2004.

5
David Mazières and M. Frans Kaashoek.
Secure applications need flexible operating systems.
In Proceedings of the 6th Workshop on Hot Topics in Operating Systems (HotOS-VI), pages 56-61, 1997.

6
Norm Hardy.
The confused deputy: (or why capabilities might have been invented).
ACM SIGOPS Operating Systems Review, 22(4):36-38, October 1988.

7
Calvin Ko and Timothy Redmond.
Noninterference and intrusion detection.
In Proceedings of the 2002 IEEE Symposium on Security and Privacy, pages 177-187, May 2002.

8
W. S. McPhee.
Operating system integrity in OS/VS2.
IBM Systems Journal, 13(3):230-252, 1974.

9
Frank Schmuck and Jim Wyllie.
Experience with transactions in QuickSilver.
In Proceedings of the 13th ACM Symposium on Operating System Principles, pages 239-253, October 1991.

10
Benjamin Schwarz, Hao Chen, David Wagner, Geoff Morrison, Jacob West, Jeremy Lin, and Wei Tu.
Model checking an entire Linux distribution for security violations.
Technical Report UCB//CSD-05-1384, UC Berkeley, April 2005.

11
W. Richard Stevens.
Unix Network Programming, chapter 14.7: Passing Descriptors.
Prentice Hall PTR, 1997.

12
Eugene Tsyrklevich and Bennet Yee.
Dynamic detection and prevention of race conditions in file accesses.
In Proceedings of the 12th Usenix Security Symposium, pages 243-255, August 2003.

About this document ...

Fixing Races for Fun and Profit: How to abuse atime

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.48)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -local_icons -antialias -antialias_text -white races.tex

The translation was initiated by Rob Johnson on 2005-05-31

Footnotes

... queue.1
This example is inspired by an actual vulnerability in lpr in Red Hat, see https://www.redhat.com/archives/redhat-watch-list/1999-October/msg00012.html.
... resolution.2
Some NFS configurations do not update link access times, but every local filesystem we tested exhibited this behavior. Some kernels support a noatime mount option that disables access time updates. Access time polling is not critical to our attack, though. The system call distinguishers we develop in Section 7 can be used instead of access time polling to synchronize with the basic $ k$-Race algorithm.
... lookups.''3
Comment in fs/namei.c. Note that this is not the same limit that is used to prevent symbolic link loops, since each symbolic link lookup is within a different component of the path.
... 2>&14
We have found this method more reliable if the grep command searches the files on the same disk as the mazes. This is likely to be a consequence of on-disk caching.
next_inactive up previous
Rob Johnson 2005-05-31