|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Security 2002 Paper
[Security '02 Tech Program Index]
Secure History Preservation through
|
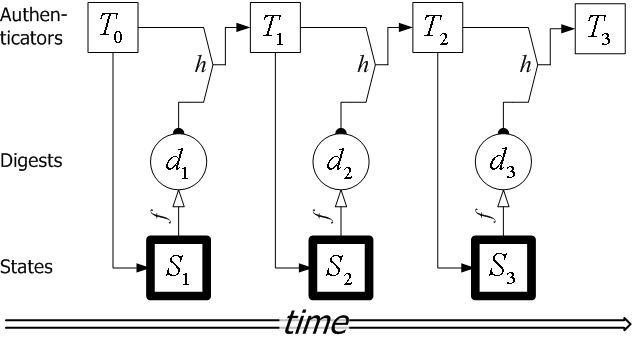 |
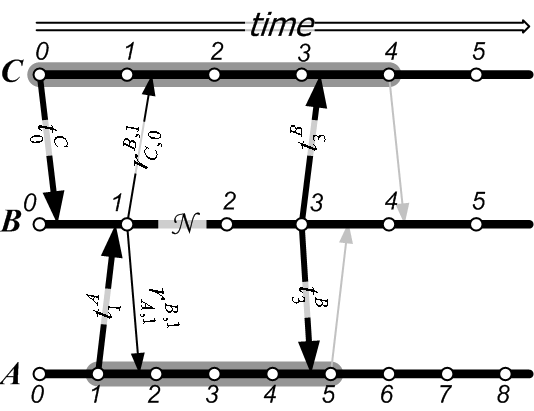
Figure 1 illustrates the first few time steps of a secure timeline. In the figure, the new timeline authenticator is also fed into the new state of the system. Depending on the definition of the state digest function, a new state of the service can be shown to be fresh, i.e., to have followed the computation of the authenticator for the previous time step. In Time Stamping Services, this places the time stamp of a document between two rounds of the service. In the Key Archival Service, this bounds the time interval during which a change in the Certification Authority (new certificate, revocation, or refresh) has occurred. In a CRT timeline system, this bounds the time when a revocation database was built. Some authenticated dictionaries can be shown to be fresh(e.g., [8]), and we explain how we handle freshness in Section 5.2.
Secure timelines can be used to answer two basic kinds of questions:
existence questions and temporal precedence questions.
Existence questions are of the form ``is ![]() the
the ![]() -th system
state?'', and are used to establish that the service exhibited a
certain kind of behavior at a particular phase in its history. In
the time stamping example, an existence question could be ``is
-th system
state?'', and are used to establish that the service exhibited a
certain kind of behavior at a particular phase in its history. In
the time stamping example, an existence question could be ``is ![]() the round hash at time
the round hash at time ![]() ?'' A positive answer allows a client to
verify the validity of a time stamp from round
?'' A positive answer allows a client to
verify the validity of a time stamp from round ![]() , since time
stamps from round
, since time
stamps from round ![]() are authenticated with the root hash of that
round. Temporal precedence questions are of the form ``did state
are authenticated with the root hash of that
round. Temporal precedence questions are of the form ``did state
![]() occur before state
occur before state ![]() ?''. In time stamping, answers to
precedence questions can establish precedence between two time
stamped documents.
?''. In time stamping, answers to
precedence questions can establish precedence between two time
stamped documents.
Answers to both existence and temporal precedence questions are
provable. Given the last authenticator in the timeline, to prove
the existence of a state in the timeline's past I have to produce a
one-way path--a sequence of applications of one-way
functions--from that state to the current timeline authenticator.
Similarly, to prove that state ![]() precedes state
precedes state ![]() , I have to
show that there exists a one-way path from state
, I have to
show that there exists a one-way path from state ![]() to state
to state ![]() .
For example, in Figure 1, the path from
.
For example, in Figure 1, the path from ![]() to
to
![]() ,
, ![]() and then to
and then to ![]() is one-way and establishes that state
is one-way and establishes that state
![]() occurred before
occurred before ![]() . Extending this path to
. Extending this path to ![]() provides
an existence proof for state
provides
an existence proof for state ![]() , if the verifier knows that
, if the verifier knows that ![]() is the latest timeline authenticator.
is the latest timeline authenticator.
Secure timelines are a general mechanism for temporal
authentication. As with any other authentication mechanism,
timeline proofs are useful only if the authenticator against which
they are validated is itself secure and easily accessible to all
verifiers, i.e., the clients within the service domain. In other
words, clients must be able to receive securely authenticator tuples
of the form
![]() from the service at every time
step, or at coarser intervals. This assumes that clients have a
means to open authenticated channels to the service. Furthermore,
there must be a unique tuple for every time step
from the service at every time
step, or at coarser intervals. This assumes that clients have a
means to open authenticated channels to the service. Furthermore,
there must be a unique tuple for every time step ![]() . Either the
service must be trusted by the clients to maintain a unique
timeline, or the timeline must be periodically ``anchored'' on an
unconditionally trusted write-once publication medium, such as a
paper journal or popular newspaper. The latter technique is used by
some commercial time stamping services [25], to reduce the
clients' need to trust the service.
. Either the
service must be trusted by the clients to maintain a unique
timeline, or the timeline must be periodically ``anchored'' on an
unconditionally trusted write-once publication medium, such as a
paper journal or popular newspaper. The latter technique is used by
some commercial time stamping services [25], to reduce the
clients' need to trust the service.
For the remainder of this paper, ``time ![]() '' means the state of the
service that is current right before timeline element
'' means the state of the
service that is current right before timeline element ![]() has been
published, as well as the physical time period between the
publication of the timeline authenticators for time steps
has been
published, as well as the physical time period between the
publication of the timeline authenticators for time steps ![]() and
and
![]() . For service
. For service ![]() , we denote time
, we denote time ![]() as
as
![]() ,
the associated timeline authenticator as
,
the associated timeline authenticator as ![]() and the precedence
proof from
and the precedence
proof from ![]() to
to ![]() as
as ![]() .
.
In the previous section, we describe how a secure timeline can be used by the clients within a service domain to reason about the temporal ordering of the states of the service in a provable manner. In so doing, the clients of the service have access to tamper-evident historic information about the operation of the service in the past.
However, the timeline of service ![]() does not carry much conviction
before a client who belongs to a different, disjoint service domain
does not carry much conviction
before a client who belongs to a different, disjoint service domain
![]() , i.e., a client who does not trust service
, i.e., a client who does not trust service ![]() or the means by
which it is held accountable. Consider an example from time
stamping where Alice, a client of TSS
or the means by
which it is held accountable. Consider an example from time
stamping where Alice, a client of TSS ![]() , wishes to know when Bob,
a client of another TSS
, wishes to know when Bob,
a client of another TSS ![]() , time stamped a particular document
, time stamped a particular document
![]() . A time stamping proof that links
. A time stamping proof that links ![]() to an
authenticator in
to an
authenticator in ![]() 's timeline only is not convincing or useful to
Alice, since she has no way to compare temporally time steps in
's timeline only is not convincing or useful to
Alice, since she has no way to compare temporally time steps in
![]() 's timeline to her own timeline, held by
's timeline to her own timeline, held by ![]() .
.
This is the void that timeline entanglement fills. Timeline entanglement creates a provable temporal precedence from a time step in a secure timeline to a time step in another independent timeline. Its objective is to allow a group of mutually distrustful service domains to collaborate towards maintaining a common, tamper-evident history of their collective timelines that can be verified from the point of view (i.e., within the trust domain) of any one of the participants.
In timeline entanglement, each participating service domain maintains its own secure timeline, but also keeps track of the timelines of other participants, by incorporating authenticators from those foreign timelines into its own service state, and therefore its own timeline. In a sense, all participants enforce the commitment of the timeline authenticators of their peers.
In Section 4.1, we define timeline entanglement with illustrative examples and outline its properties. We then explore in detail three aspects of timeline entanglement: Secure Temporal Mappings in Section 4.2, the implications of dishonest timeline maintainers in Section 4.3, and Historic Survivability in Section 4.4.
Timeline entanglement is defined within the context of an entangled service set. This is a dynamically changing set of service domains. Although an entangled service set where all participating domains offer the same kind of service is conceivable--such as, for example, a set of time stamping services--we envision many different service types, time stamping services, certification authorities, historic records services, etc., participating in the same entangled set. We assume that all participating services know the current membership of the entangled service set, although inconsistencies in this knowledge among services does not hurt the security of our constructs below. We also assume that members of the service set can identify and authenticate each other, either through the use of a common public key infrastructure, or through direct out-of-band key exchanges.
Every participating service defines an independent sampling method
to select a relatively small subset of its logical time steps for
entanglement. For example, a participant can choose to entangle
every ![]() -th time step. At every time step picked for entanglement,
the participant sends an authenticated message that contains its
signed logical time and timeline authenticator to all other
participants in the entangled service set. This message is called a
timeline thread. A timeline thread sent from
-th time step. At every time step picked for entanglement,
the participant sends an authenticated message that contains its
signed logical time and timeline authenticator to all other
participants in the entangled service set. This message is called a
timeline thread. A timeline thread sent from ![]() at time
at time
![]() is denoted as
is denoted as ![]() and has the form
and has the form
![]() .
. ![]() represents
represents
![]() 's signature on message
's signature on message ![]() .
.
When participant ![]() receives a correctly signed timeline thread
from participant
receives a correctly signed timeline thread
from participant ![]() , it verifies the consistency of that thread
with its local view of collective history and then archives it.
Thread
, it verifies the consistency of that thread
with its local view of collective history and then archives it.
Thread ![]() is consistent with
is consistent with ![]() 's local view of collective
history if it can be proved to be on the same one-way path (hash
chain) as the last timeline authenticator of
's local view of collective
history if it can be proved to be on the same one-way path (hash
chain) as the last timeline authenticator of ![]() that
that ![]() knows
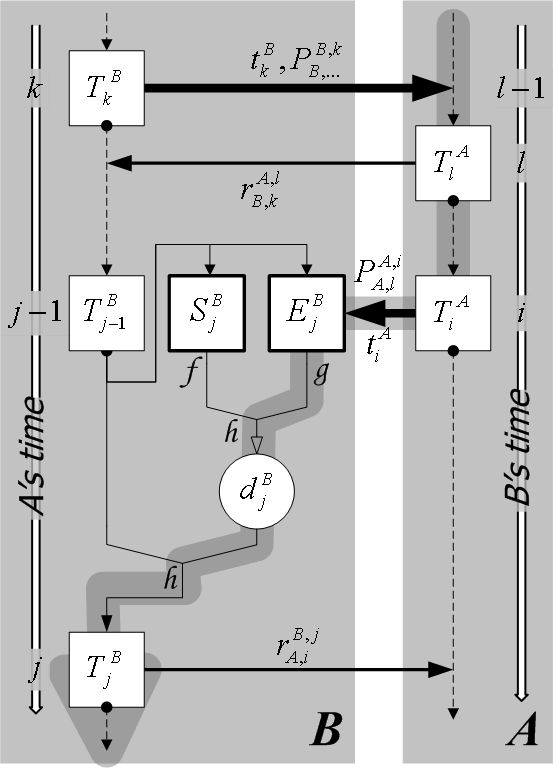
about (see Figure 2). Towards this goal,
knows
about (see Figure 2). Towards this goal, ![]() includes the necessary temporal precedence proof, as described in
Section 3, along with the thread that it sends to
includes the necessary temporal precedence proof, as described in
Section 3, along with the thread that it sends to
![]() . In the figure, when thread
. In the figure, when thread ![]() reaches
reaches ![]() , the most
recent timeline authenticator of
, the most
recent timeline authenticator of ![]() that
that ![]() knows is
knows is ![]() .
Along with the thread,
.
Along with the thread, ![]() sends the precedence proof
sends the precedence proof
![]() from its time
from its time
![]() to time
to time
![]() . As a result,
. As a result, ![]() can verify that the new thread
carries a ``legitimate'' timeline authenticator from
can verify that the new thread
carries a ``legitimate'' timeline authenticator from ![]() , one
consistent with history. If everything checks out,
, one
consistent with history. If everything checks out, ![]() archives the
new timeline authenticator and associated precedence proof in its
local thread archive.
archives the
new timeline authenticator and associated precedence proof in its
local thread archive.
Thread archives store tuples of the form
![]() . A
thread archive serves two purposes: first, it maintains a
participant's local knowledge of the history of the entangled
service set. Specifically, it archives proof that every participant
it knows about maintains a consistent timeline. It accomplishes
this by simply storing the threads, which are snapshots in the
sender's timeline, and supporting precedence proofs, which connect
these snapshots in a single one-way chain. The second purpose of
the thread archive is to maintain temporal precedence proofs between
every foreign thread it contains and local timeline steps. It
accomplishes this by constructing a one-way digest of its contents
as they change, and then using that digest along with the system
state digest, to derive the next local timeline authenticator
(Section 5.2 describes how the thread archive is
implemented). In the figure,
. A
thread archive serves two purposes: first, it maintains a
participant's local knowledge of the history of the entangled
service set. Specifically, it archives proof that every participant
it knows about maintains a consistent timeline. It accomplishes
this by simply storing the threads, which are snapshots in the
sender's timeline, and supporting precedence proofs, which connect
these snapshots in a single one-way chain. The second purpose of
the thread archive is to maintain temporal precedence proofs between
every foreign thread it contains and local timeline steps. It
accomplishes this by constructing a one-way digest of its contents
as they change, and then using that digest along with the system
state digest, to derive the next local timeline authenticator
(Section 5.2 describes how the thread archive is
implemented). In the figure, ![]() 's system state
's system state ![]() and updated
thread archive
and updated
thread archive ![]() are combined into
are combined into ![]() , which then
participates in the computation of the next timeline authenticator
, which then
participates in the computation of the next timeline authenticator
![]() .
.
 |
Participant ![]() responds to the newly reported timeline
authenticator with an entanglement receipt. This receipt
proves that the next timeline authenticator that
responds to the newly reported timeline
authenticator with an entanglement receipt. This receipt
proves that the next timeline authenticator that ![]() produces is
influenced partly by the archiving of the thread it just received.
The receipt must convince
produces is
influenced partly by the archiving of the thread it just received.
The receipt must convince ![]() of three things: first, that its
thread was archived; second, that the thread was archived in the
latest--``freshest''--version of
of three things: first, that its
thread was archived; second, that the thread was archived in the
latest--``freshest''--version of ![]() 's thread archive; and, third,
that this version of the thread archive is the one whose digest is
used to derive the next timeline authenticator that
's thread archive; and, third,
that this version of the thread archive is the one whose digest is
used to derive the next timeline authenticator that ![]() produces.
As a result, the entanglement receipt
produces.
As a result, the entanglement receipt ![]() that
that ![]() returns to
returns to ![]() for the entanglement of thread
for the entanglement of thread ![]() consists of
three components: first, a precedence proof
consists of
three components: first, a precedence proof
![]() from
the last of
from
the last of ![]() 's timeline authenticators that
's timeline authenticators that ![]() knows about,
knows about,
![]() , to
, to ![]() 's timeline authenticator
's timeline authenticator ![]() right before
archiving
right before
archiving ![]() 's new thread; second, an existence proof showing that
the timeline thread
's new thread; second, an existence proof showing that
the timeline thread ![]() is archived in the latest, freshest
version
is archived in the latest, freshest
version ![]() of
of ![]() 's thread archive after the last
authenticator
's thread archive after the last
authenticator ![]() was computed; and, third, a one-way
derivation of the next timeline authenticator of
was computed; and, third, a one-way
derivation of the next timeline authenticator of ![]() from the new
version of the thread archive and the current system state
from the new
version of the thread archive and the current system state ![]() .
It is now
.
It is now ![]() 's turn to check the validity of the proofs in the
entanglement receipt. If all goes well,
's turn to check the validity of the proofs in the
entanglement receipt. If all goes well, ![]() stores the proof of
precedence and reported timeline authenticator from
stores the proof of
precedence and reported timeline authenticator from ![]() in its
receipt archive. This concludes the entanglement process
from time
in its
receipt archive. This concludes the entanglement process
from time
![]() to time
to time
![]() .
.
The receipt archive is similar to the thread archive; it stores entanglement receipts that the participant receives in response to its own timeline threads.
After the entanglement of time
![]() with time
with time
![]() , both
, both ![]() and
and ![]() have in their possession
portable temporal precedence proofs ordering
have in their possession
portable temporal precedence proofs ordering ![]() 's past before
's past before ![]() 's
future. Any one-way process at
's
future. Any one-way process at ![]() whose result is included in the
derivation of
whose result is included in the
derivation of ![]() or earlier timeline authenticators at
or earlier timeline authenticators at ![]() can
be shown to have completed before any one-way process at
can
be shown to have completed before any one-way process at ![]() that
includes in its inputs
that
includes in its inputs ![]() or later timeline authenticators at
or later timeline authenticators at
![]() .
.
In this definition of timeline entanglement, a participating service entangles its timeline at the predetermined sample time steps with all other services in the entangled service set (we call this all-to-all entanglement). In this work we limit the discussion to all-to-all entanglement only, but we describe a more restricted, and consequently less expensive, entanglement model in future work (Section 7).
The primary benefit of timeline entanglement is its support for secure temporal mapping. A client in one service domain can use temporal information maintained in a remote service domain that he does not trust, by mapping that information onto his own service domain. This mapping results in some loss of temporal resolution--for example, a time instant maps to a positive-length time interval. We describe secure temporal mapping in Section 4.2.
Timeline entanglement is a sound method of expanding temporal precedence proofs outside a service domain; it does not prove incorrect precedences. However it is not complete, that is, there are some precedences it cannot prove. For example, it is possible for a dishonest service to maintain clandestinely two timelines, essentially ``hiding'' the commitment of some of its system states from some members of the entangled service set. We explore the implications of such behavior in Section 4.3.
Finally, we consider the survivability characteristics of temporal proofs beyond the lifetime of the associated timeline, in Section 4.4.
Temporal mapping allows a participating service ![]() to map onto its
own timeline a time step
to map onto its
own timeline a time step
![]() from the timeline of
another participant
from the timeline of
another participant ![]() . This mapping is denoted by
. This mapping is denoted by
![]() . Since
. Since ![]() and
and ![]() do not trust each other,
the mapping must be secure; this means it should be practically
impossible for
do not trust each other,
the mapping must be secure; this means it should be practically
impossible for ![]() to prove to
to prove to ![]() that
that
![]() , if
, if
![]() occurred before or at
occurred before or at
![]() , or after
, or after
![]() .
.
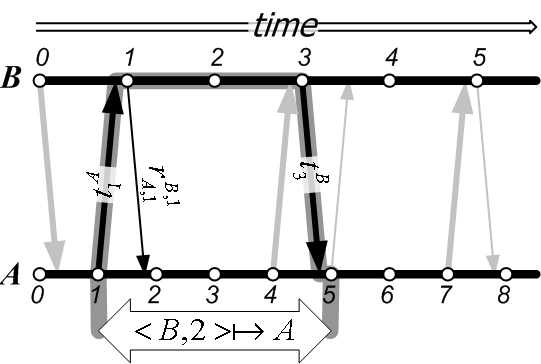
Figure 3 illustrates the secure temporal mapping
![]() . To compute the mapping,
. To compute the mapping, ![]() requires
only local information from its thread and receipt archives. First,
it searches in its receipt archive for the latest entanglement
receipt that
requires
only local information from its thread and receipt archives. First,
it searches in its receipt archive for the latest entanglement
receipt that ![]() sent back before or at time
sent back before or at time
![]() ,
receipt
,
receipt ![]() in the example. As described in
Section 4, this receipt proves to
in the example. As described in
Section 4, this receipt proves to ![]() that its
time
that its
time
![]() occurred before
occurred before ![]() 's time
's time
![]() .
.
Then, ![]() searches in its thread archive for the earliest thread
that
searches in its thread archive for the earliest thread
that ![]() sent it after time
sent it after time
![]() , which is thread
, which is thread
![]() in the example. This thread proves to
in the example. This thread proves to ![]() that its time
that its time
![]() occurred at or after time
occurred at or after time
![]() .
Recall, also, that when
.
Recall, also, that when ![]() received
received ![]() in the first place, it
had also received a temporal precedence proof from
in the first place, it
had also received a temporal precedence proof from
![]() to
to
![]() , which in the straightforward
hash chain case, also includes the system state digest for
, which in the straightforward
hash chain case, also includes the system state digest for
![]() . Now
. Now ![]() has enough information to conclude that
has enough information to conclude that
![]() .
.
Since ![]() has no reason to believe that
has no reason to believe that ![]() maintains its timeline
in regular intervals, there is no more that
maintains its timeline
in regular intervals, there is no more that ![]() can assume about the
temporal placement of state
can assume about the
temporal placement of state ![]() within the interval
within the interval
![]() . This results in a loss of
temporal resolution; in the figure, this loss is illustrated as the
difference between the length on
. This results in a loss of
temporal resolution; in the figure, this loss is illustrated as the
difference between the length on ![]() 's timeline from
's timeline from
![]() to
to
![]() (i.e., the ``duration'' of time
step
(i.e., the ``duration'' of time
step
![]() ) and the length of the segment on
) and the length of the segment on ![]() 's
timeline from
's
timeline from
![]() to
to
![]() (the
duration of
(the
duration of
![]() ). This loss is higher
when
). This loss is higher
when ![]() and
and ![]() exchange thread messages infrequently. It can be
made lower, but only at the cost of increasing the frequency with
which
exchange thread messages infrequently. It can be
made lower, but only at the cost of increasing the frequency with
which ![]() and
and ![]() send threads to each other, which translates to
more messages and more computation at
send threads to each other, which translates to
more messages and more computation at ![]() and
and ![]() . We explore this
trade-off in Section 6.
. We explore this
trade-off in Section 6.
 |
Secure time mapping allows clients within a service domain to
determine with certainty the temporal ordering between states on
their own service and on remote, untrusted service domains. Going
back to the time stamping example, assume that Alice has in her
possession a time stamp for document ![]() in her own
service domain
in her own
service domain ![]() , which links it to local time
, which links it to local time
![]() , and she has been presented by Bob with a time stamp on
document
, and she has been presented by Bob with a time stamp on
document ![]() in his service domain
in his service domain ![]() , which links Bob's
document to time
, which links Bob's
document to time
![]() . Alice can request from
. Alice can request from ![]() the time mapping
the time mapping
![]() , shown above to be
, shown above to be
![]() . With this information,
Alice can be convinced that her document
. With this information,
Alice can be convinced that her document ![]() was time
stamped after Bob's document
was time
stamped after Bob's document ![]() was, regardless of
whether or not Alice trusts Bob or
was, regardless of
whether or not Alice trusts Bob or ![]() .
.
In the general case, not all time steps in one timeline map readily to another timeline. To reduce the length of temporal precedence proofs, we use hash skip lists (Section 5.1) instead of straightforward hash chains in Timeweave, our prototype. Temporal precedence proofs on skip lists are shorter because they do not contain every timeline authenticator from the source to the destination. In timelines implemented in this manner, only time steps included in the skip list proof can be mapped without the cooperation of the remote service. For other mappings, the remote service must supply additional, more detailed precedence proofs, connecting the time authenticator in question to the time authenticators that the requester knows about.
Timeline entanglement is intended as an artificial enlargement of the class of usable, temporal orderings that clients within a service domain can determine undeniably. Without entanglement, a client can determine the provable ordering of events only on the local timeline. With entanglement, one-way paths are created that anchor time segments from remote, untrusted timelines onto the local timeline.
However, the one-way properties of the digest and hash functions used make timelines secure only as long as everybody is referring to the same, single timeline. If, instead, a dishonest service maintains clandestinely two or more timelines or branches of the same timeline, publishing different timeline authenticators to different subsets of its users, then that service can, in a sense, revise history. Just [12] identified such an attack against early time stamping services. Within a service domain, this attack can be foiled by enforcing that the service periodically commit its timeline on a write-once, widely published medium, such as a local newspaper or paper journal. When there is doubt, a cautious client can wait to see the precedence proof linking the timeline authenticator of interest to the next widely published authenticator, before considering the former unique.
Unfortunately, a similar attack can be mounted against the integrity
of collective history, in an entangled service set. Entanglement,
as described in Section 4, does not verify that
samples from ![]() 's timeline that are archived at
's timeline that are archived at ![]() and
and ![]() are
identical. If
are
identical. If ![]() is malicious, it can report authenticators from
one chain to
is malicious, it can report authenticators from
one chain to ![]() and from another to
and from another to ![]() , undetected (see
Figure 4). In the general case, this does not
dilute the usability of entanglement among honest service domains.
Instead, it renders unprovable some interactions between honest and
dishonest service domains. More importantly, attacks by a service
against the integrity of its own timeline can only make external
temporal precedence information involving that timeline
inconclusive; such attacks cannot change the temporal ordering
between time steps on honest and dishonest timelines. Ultimately,
it is solely the clients of a dishonest service who suffer the
consequences.
, undetected (see
Figure 4). In the general case, this does not
dilute the usability of entanglement among honest service domains.
Instead, it renders unprovable some interactions between honest and
dishonest service domains. More importantly, attacks by a service
against the integrity of its own timeline can only make external
temporal precedence information involving that timeline
inconclusive; such attacks cannot change the temporal ordering
between time steps on honest and dishonest timelines. Ultimately,
it is solely the clients of a dishonest service who suffer the
consequences.
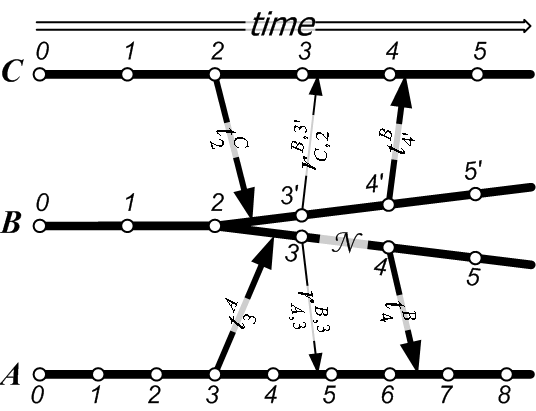 |
Consider, for instance, the scenario of Figure 4.
Dishonest service ![]() has branched off its originally unique
timeline into two separate timelines at its time
has branched off its originally unique
timeline into two separate timelines at its time
![]() . It uses the top branch, with times
. It uses the top branch, with times ![]() ,
, ![]() , etc.,
in its entanglements with service
, etc.,
in its entanglements with service ![]() , and its bottom branch, with
times
, and its bottom branch, with
times ![]() ,
, ![]() , etc., in its entanglements with service
, etc., in its entanglements with service ![]() . From
. From
![]() 's point of view, event
's point of view, event ![]() is incorporated in
is incorporated in ![]() 's
state and corresponding timeline at time
's
state and corresponding timeline at time
![]() . From
. From
![]() 's point of view, however, event
's point of view, however, event ![]() seems never to
have happened. Since
seems never to
have happened. Since ![]() does not appear in the branch of
does not appear in the branch of
![]() 's timeline that is visible to
's timeline that is visible to ![]() ,
, ![]() 's clients cannot
conclusively place event
's clients cannot
conclusively place event ![]() in time at all. Therefore,
only the client of
in time at all. Therefore,
only the client of ![]() who is responsible for event
who is responsible for event ![]() suffers from this discrepancy.
suffers from this discrepancy. ![]() does not know about it at all,
and
does not know about it at all,
and ![]() knows its correct relative temporal position.
knows its correct relative temporal position.
We describe briefly a method for enforcing timeline uniqueness within an entangled service set in Section 7.
Historic survivability in the context of an entangled set of services is the decoupling of the verifiability of existence and temporal precedence proofs within a timeline from the fate of the maintainer of that timeline.
Temporal proofs are inherently survivable because of their dependence on well-known, one-way constructs. For example, a hash chain consisting of multiple applications of SHA-1 certainly proves that the result of the chain temporally followed the input to the chain. However, this survivability is moot, if the timeline authenticators that the proof orders undeniably can no longer be interpreted or associated with a real time frame.
Fortunately, secure temporal mapping allows a client within a service domain to fortify a temporal proof that he cares about against the passing of the local service. The client can accomplish this by participating in more service domains than one; then, he can proactively map the temporal proofs he cares about from their source timeline onto all the timelines of the service domains in which he belongs. In this manner, even if all but one of the services with which he is associated become unavailable or go out of business, the client may still associate his proofs with a live timeline in the surviving service domain.
Consider, for example, the scenario illustrated in
Figure 5. David, who belongs to all three
service domains ![]() ,
, ![]() and
and ![]() , wishes to fortify event
, wishes to fortify event
![]() so as to be able to place it in time, even if service
so as to be able to place it in time, even if service
![]() is no longer available. He maps the event onto the timelines of
is no longer available. He maps the event onto the timelines of
![]() and
and ![]() --``mapping an event
--``mapping an event ![]() '' is equivalent to
mapping the timeline time step in whose system state event
'' is equivalent to
mapping the timeline time step in whose system state event
![]() is included, that is,
is included, that is,
![]() in the
example. Even though the event occurred in
in the
example. Even though the event occurred in ![]() 's timeline, David
can still reason about its relative position in time, albeit with
some loss of resolution, in both the service domains of
's timeline, David
can still reason about its relative position in time, albeit with
some loss of resolution, in both the service domains of ![]() and
and ![]() ,
long after
,
long after ![]() is gone. In a sense, David ``hedges his bets'' among
multiple services, hoping that one of them survives. Note also that
the fortification of even
is gone. In a sense, David ``hedges his bets'' among
multiple services, hoping that one of them survives. Note also that
the fortification of even ![]() can occur long after its
occurrence. The use of temporal mapping in this context is similar
in scope to the techniques used by Ansper et al. [2]
for fault-tolerant time stamping services, although it assumes far
less mutual trust among the different service domains.
can occur long after its
occurrence. The use of temporal mapping in this context is similar
in scope to the techniques used by Ansper et al. [2]
for fault-tolerant time stamping services, although it assumes far
less mutual trust among the different service domains.
We have devised two new, to our knowledge, disk-oriented data structures for the implementation of Timeweave, our timeline entanglement prototype. In Section 5.1, we present authenticated append-only skip lists. These are an efficient optimization of traditional hash chains and yield precedence proofs with size proportional to the square logarithm of the total elements in the list, as opposed to linear. In Section 5.2, we present RBB-Trees, our disk-based, persistent authenticated dictionaries based on authenticated search trees. RBB-Trees scale to larger sizes than current in-memory persistent authenticated dictionaries, while making efficient use of the disk. Finally, in Section 5.3, we outline how Timeweave operates.
 |
Our basic tool for maintaining an efficient secure timeline is the authenticated append-only skip list. The authenticated append-only skip list is a modification of the simplistic hash chain described in Section 3 that yields improved access characteristics and shorter proofs.
Our skip lists are deterministic, as opposed to the randomized skip
lists proposed in the literature [20]. Unlike the
authenticated skip lists introduced by Goodrich et
al. [10], our skip lists are append-only, which
obviates the need for commutative hashing. Every list element has a
numeric identifier that is a counter from the first element in the
list (the first element is element ![]() , the tenth element is element
, the tenth element is element
![]() , and so on); the initial authenticator of the skip list before
any elements are inserted is element
, and so on); the initial authenticator of the skip list before
any elements are inserted is element ![]() . Every inserted element
carries a data value and an authenticator, similarly to what was
suggested in Section 3 for single-chain timelines.
. Every inserted element
carries a data value and an authenticator, similarly to what was
suggested in Section 3 for single-chain timelines.
The skip list consists of multiple parallel hash chains at different
levels of detail, each containing half as many elements as the
previous one. The basic chain (at level 0) links every
element to the authenticator of the one before it, just like simple
hash chains. The next chain (at level 1) coexists with the level 0
chain, but only contains elements whose numeric identifiers are
multiples of 2, and every element is linked to the element two
positions before it. Similarly, only elements with numeric
identifiers that are multiples of ![]() are contained in the hash
chain of level
are contained in the hash
chain of level ![]() . No chains of level
. No chains of level ![]() are maintained,
if all elements are
are maintained,
if all elements are ![]() .
.
The authenticator ![]() of element
of element ![]() with data value
with data value ![]() is
computed from a hash of all the partial authenticators (called
links) from each basic hash chain in which the element
participates. Element
is
computed from a hash of all the partial authenticators (called
links) from each basic hash chain in which the element
participates. Element ![]() , where
, where ![]() does not divide
does not divide ![]() ,
participates in
,
participates in ![]() chains. It has the
chains. It has the ![]() links
links
![]() ,
, ![]() , and authenticator
, and authenticator
![]() . Figure 6
illustrates a portion of such a skip list. In the implementation,
we combine together the element authenticator with the 0-th level
link for odd-numbered elements, since such elements have a single
link, which is sufficient as an authenticator by itself.
. Figure 6
illustrates a portion of such a skip list. In the implementation,
we combine together the element authenticator with the 0-th level
link for odd-numbered elements, since such elements have a single
link, which is sufficient as an authenticator by itself.
 |
Skip lists allow their efficient traversal from an element ![]() to a
later element
to a
later element ![]() in a logarithmic number of steps: starting from
element
in a logarithmic number of steps: starting from
element ![]() , successively higher-level links are utilized until the
``tallest element'' (one with the largest power of 2 in its factors
among all element indices between
, successively higher-level links are utilized until the
``tallest element'' (one with the largest power of 2 in its factors
among all element indices between ![]() and
and ![]() ) is reached.
Thereafter, successively lower-level links are traversed until
) is reached.
Thereafter, successively lower-level links are traversed until ![]() is reached. More specifically, an iterative process starts with the
current element
is reached. More specifically, an iterative process starts with the
current element ![]() . To move closer to the destination element
with index
. To move closer to the destination element
with index ![]() , the highest power
, the highest power ![]() of 2 that divides
of 2 that divides ![]() is
picked, such that
is
picked, such that ![]() . Then element
. Then element ![]() becomes the
next current element
becomes the
next current element ![]() in the traversal. The iteration stops when
in the traversal. The iteration stops when
![]() .
.
The associated temporal precedence proof linking element ![]() before
element
before
element ![]() is constructed in a manner similar to the traversal
described above. At every step, when a jump of length
is constructed in a manner similar to the traversal
described above. At every step, when a jump of length ![]() is
taken from the current element
is
taken from the current element ![]() to
to ![]() , the element value
of the new element
, the element value
of the new element ![]() is appended to the proof, along with all
the associated links of element
is appended to the proof, along with all
the associated links of element ![]() , except for the link at level
, except for the link at level
![]() . Link
. Link ![]() is omitted since it can be computed during
verification from the previous authenticator
is omitted since it can be computed during
verification from the previous authenticator ![]() and the data
value
and the data
value ![]() .
.
In the example of Figure 6, the path from element
![]() to element
to element ![]() traverses elements
traverses elements ![]() and
and ![]() . The
corresponding precedence proof from element
. The
corresponding precedence proof from element ![]() to element
to element ![]() is
is
![]() .
With this proof and given the authenticators
.
With this proof and given the authenticators ![]() and
and ![]() of elements
of elements ![]() and
and ![]() respectively, the verifier can
successively compute
respectively, the verifier can
successively compute
![]() , then
, then
![]() and
finally
and
finally
![]() --recall that for all
odd elements
--recall that for all
odd elements ![]() ,
, ![]() . If the known and the derived values
for the authenticator agree (
. If the known and the derived values
for the authenticator agree (
![]() ), then the verifier
can be convinced that the authenticator
), then the verifier
can be convinced that the authenticator ![]() preceded the
computation of authenticator
preceded the
computation of authenticator ![]() , which is the objective of a
precedence proof.
, which is the objective of a
precedence proof.
Thanks to the properties of skip lists, any of these proofs contains
links and data values of roughly a logarithmic number of skip list
elements. The worst-case proof for a skip list of ![]() elements
traverses
elements
traverses
![]() elements, climbing links of every
level between
elements, climbing links of every
level between ![]() and
and ![]() and back down again, or
and back down again, or
![]() link values and
link values and ![]() data values total.
Assuming that every link and value is a SHA-1 digest of 160 bits,
the worst case proof for a timeline of a billion elements is no
longer than 20 KBytes, and most are much shorter.
data values total.
Assuming that every link and value is a SHA-1 digest of 160 bits,
the worst case proof for a timeline of a billion elements is no
longer than 20 KBytes, and most are much shorter.
Our skip lists are fit for secondary storage. They are implemented on memory-mapped files. Since modifications are expected to be relatively rare, compared to searches and proof extractions, we always write changes to the skip list through to the disk immediately after they are made, to maintain consistency in the face of machine crashes. We do not, however, support structural recovery from disk crashes; we believe that existing file system and redundant disk array technologies are adequate to prevent and recover all but the most catastrophic losses of disk bits.
This work uses authenticated persistent dictionaries based on trees.
A persistent dictionary maintains multiple versions (or
snapshots) of its contents as it is modified. In addition to
the functionality offered by simple authenticated dictionaries, it
can also provably answer questions of the form ``in snapshot ![]() ,
was element
,
was element ![]() in the dictionary?''.
in the dictionary?''.
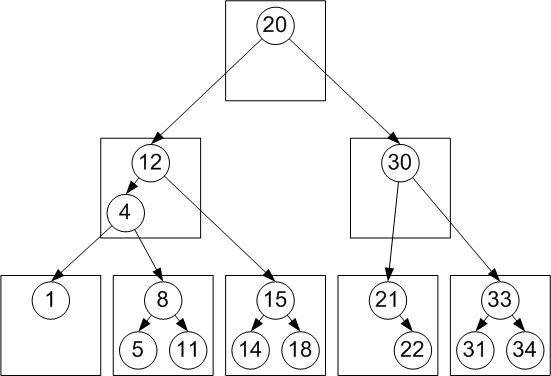
The dictionaries we use in this work can potentially grow very large, much larger than the sizes of current main memories. Therefore, we have extended our earlier work on balanced persistent authenticated search trees [16] to design on-disk persistent authenticated dictionaries. The resulting data structure, the RBB-Tree, is a binary authenticated search tree [6,7] embedded in a persistent B-Tree [4][9, Ch. 18]. Figure 7 shows a simple RBB-Tree holding 16 numeric keys.
 |
RBB-Trees, like B-Trees, are designed to organize keys together in
efficient structures that result in few disk accesses per tree
operation. Every tree node is stored in its own disk block,
contains a minimum of ![]() and a maximum of
and a maximum of ![]() keys, and has
between
keys, and has
between ![]() and
and ![]() children (the root node is only required to
have between
children (the root node is only required to
have between ![]() and
and ![]() keys). Parameter
keys). Parameter ![]() is the order
of the B-Tree.
is the order
of the B-Tree.
Unlike traditional B-Trees, RBB-Tree nodes do not store their keys in a flat array. Instead, keys within RBB nodes are organized in a balanced binary tree, specifically a red-black tree [3][9, Ch. 13]. We consider RBB-Trees ``virtual'' binary trees, since the in-node binary trees connected to each other result in a large, piecewise-red-black tree, encompassing all keys in the entire dictionary.
It is this ``virtual'' binary tree of keys that is authenticated, in the sense of the authenticated search trees by Buldas et al. [6,7]. As such, the security properties of RBB-Trees are identical to those of authenticated search trees, including the structure of existence/non-existence proofs.
Since the RBB-Tree is a valid B-Tree, it is efficient in the number
of disk block accesses it requires for the basic tree operations of
insertion, deletion and modification. Specifically, each of those
operations takes
![]() disk accesses, where
disk accesses, where ![]() is the total number of keys in the tree. Similarly, since the
internal binary tree in each RBB-Tree node is balanced, the virtual
embedded binary tree is also loosely balanced, and has height
is the total number of keys in the tree. Similarly, since the
internal binary tree in each RBB-Tree node is balanced, the virtual
embedded binary tree is also loosely balanced, and has height
![]() , that is,
, that is,
![]() but with a higher constant factor than in
a real red-black tree. These two collaborating types of balancing
applied to the virtual binary tree--the first through the blocking
of keys in RBB nodes, and the second through the balancing of the
key nodes inside each RBB node--help keep the length of the
resulting existence/non-existence proofs also bounded to
but with a higher constant factor than in
a real red-black tree. These two collaborating types of balancing
applied to the virtual binary tree--the first through the blocking
of keys in RBB nodes, and the second through the balancing of the
key nodes inside each RBB node--help keep the length of the
resulting existence/non-existence proofs also bounded to
![]() elements.
elements.
The internal key structure imposed on RBB-Tree nodes does not
improve the speed of search through the tree over the speed of
search in an equivalent B-Tree, but limits the length of existence
proofs immensely. The existence proof for a datum inside an
authenticated search tree consists of the search keys of each node
from the sought datum up to the root, along with the labels of the
siblings of each of the ancestors of the sought datum up to the
root [6]. In a very ``bushy'' tree, as B-Trees are
designed to be, this would mean proofs containing authentication
data from a small number of individual nodes; unfortunately, each
individual node's authentication data consist of roughly ![]() keys
and
keys
and ![]() siblings' labels. For example, a straightforwardly
implemented authenticated B-Tree storing a billion SHA-1 digests
with
siblings' labels. For example, a straightforwardly
implemented authenticated B-Tree storing a billion SHA-1 digests
with ![]() yields existence proofs of length
yields existence proofs of length
![]() bits, or roughly 160 KBits.
The equivalent red-black tree yields existence proofs of no more
than
bits, or roughly 160 KBits.
The equivalent red-black tree yields existence proofs of no more
than
![]() bits, or
about 18 KBits. RBB-Trees seek to trade off the low disk access
costs of B-Trees with the short proof lengths of red-black trees.
The equivalent RBB-Tree of one billion SHA-1 digests yields proofs
no longer than
bits, or
about 18 KBits. RBB-Trees seek to trade off the low disk access
costs of B-Trees with the short proof lengths of red-black trees.
The equivalent RBB-Tree of one billion SHA-1 digests yields proofs
no longer than
We have designed dynamic set persistence [9, p. 294] at the granularity of both the RBB node and the embedded key node (see Figure 8). As long as there is key-node space available within an RBB node, new snapshots of the key tree within that node are collocated with older snapshots. This allows multiple snapshots to share unchanged key nodes within the same RBB node. When, however, all available key-node space within an RBB node is exhausted, subsequent snapshots of the key tree inside that node are migrated to a new, fresh RBB node.
The different persistent snapshot roots of the RBB-Tree are held together in an authenticated linked list--in fact, we use our own append-only authenticated skip list from Section 5.1.
Since each snapshot of the RBB-Tree is a ``virtual'' binary authenticated search tree, the root label of that tree (i.e., the label of the root key node of the root RBB node) is a one-way digest of the snapshot [6,7]. Furthermore, the authenticated skip list of those snapshot root labels is itself a one-way digest of the sequence of snapshot roots. As a result, the label of the last element of the snapshot root skip list is a one-way digest of the entire history of operations of the persistent RBB-Tree. The snapshot root skip list subsumes the functionality of the Time Tree in our earlier persistent authenticated red-black tree design [16].
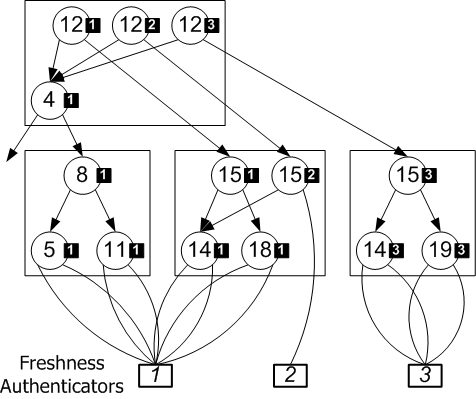 |
In some cases the ``freshness'' of an authenticated dictionary snapshot has to be provable. For example, in our description of secure timelines, we have specified that the system state must depend on the authenticator of the previous timeline time step. When the system state is represented by an authenticated dictionary, an existence proof within that dictionary need not only show that a sought element is part of the dictionary given the dictionary digest (root hash), but also that the sought element was added into the dictionary after the authenticator of the previous time step was known.
As with other authenticated dictionaries, we accomplish this by making the hash label of NIL pointers equal to the ``freshness'' authenticator, so that all existence proofs of newly inserted elements--equivalently, non-existence proofs of newly removed elements--prove that they happened after the given freshness authenticator was known. Note that subtrees of the RBB-Tree that do not change across snapshots retain their old freshness authenticators. This is acceptable, since freshness is only necessary to prove to a client that a requested modification was just performed (for example, when we produce entanglement receipts in Section 4), and is required only of newly removed or inserted dictionary elements. In the figure, the label for key node 19 is derived from the freshness authenticator for snapshot 3, since 19 is added into the tree in snapshot 3. This establishes that the tree changed to receive key 19 after the value of the freshness authenticator for snapshot 3 was known.
In standalone RBB-Trees, the freshness authenticator is simply the
last authenticator in the snapshot root list (i.e., the
authenticator that resulted from the insertion of the latest closed
snapshot root into the skip list). In the RBB-Trees that we use for
thread archives in Timeweave (Section 5.3), the
freshness authenticator for snapshot ![]() is exactly the
authenticator of the previous timeline time step
is exactly the
authenticator of the previous timeline time step ![]() .
.
Timeweave is an implementation of the timeline entanglement mechanisms described in Section 4. It is built using our authenticated append-only skip lists (Section 5.1) and our on-disk persistent authenticated search trees (Section 5.2).
A Timeweave machine maintains four components: first, a service state, which is application specific, and the one-way digest mechanism thereof; second, its secure timeline; third, a persistent authenticated archive of timeline threads received; and, fourth, a simple archive of entanglement receipts received.
The timeline is stored as an append-only authenticated skip list. The system digest used to derive the timeline authenticator at every logical time step is a hash of the concatenation of the service state digest and the digest of the thread archive after any incoming and outgoing threads have been recorded.
The thread archive contains threads sent by remote peers and verified locally. Such threads are contained both in thread messages initiated remotely and in entanglement receipts to outgoing threads. The archived threads are ordered by the identity of the remote peer in the entanglement operation, and then by the foreign logical time associated with the operation. The archive is implemented as an RBB-Tree and has a well-defined mechanism for calculating its one-way digest, described in Section 5.2.
The receipt archive is a simple (not authenticated) repository of thread storage receipts for all outgoing threads successfully acknowledged by remote peers.
The main operational loop of a Timeweave machine is as follows:
The Timeweave machine also allows clients to request local temporal mappings of remote logical times and temporal precedences between local times.
In this section, we evaluate the performance characteristics of timeline entanglement. First, in Section 6.1, we present measurements from a Java implementation of the Timeweave infrastructure: authenticated append-only skip lists and RBB-Trees. Then, in Section 6.2, we explore the performance characteristics of Timeweave as a function of its basic Timeweave system parameter, entanglement load.
In all measurements, we use a lightly loaded dual Pentium III Xeon computer at 1 GHz, with 2 GBytes of main memory, running RedHat Linux 7.2, with the stock 2.4.9-31smp kernel and Sun Microsystems' JVM 1.3.02. The three disks used in the experiments are model MAJ3364MP made by Fujitsu, which offer 10,000 RPMs and 5 ms average seek time. We use a disk block size of 64 KBytes. Finally, for signing we use DSA with SHA-1, with a key size of 1024 bits.
 |
We measure the raw performance characteristics of our disk-based authenticated data structures. Since Timeweave relies heavily on these two data structures, understanding their performance can help evaluate the performance limitations of Timeweave.
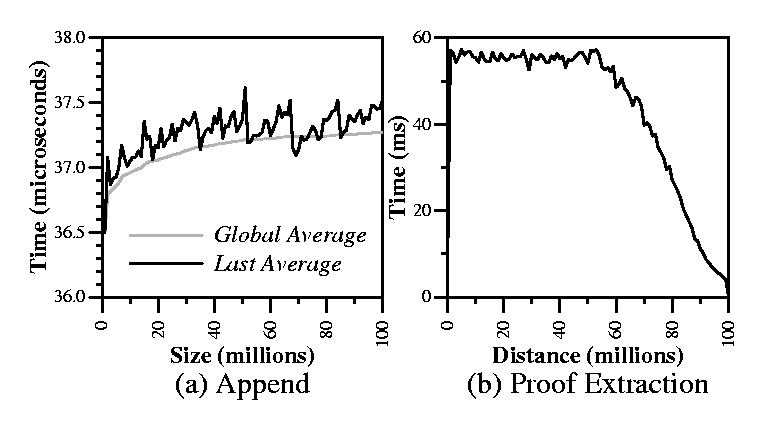
Figure 9(a) shows the performance of skip list appends, for skip list sizes ranging from one million to 100 million elements, in increments of one million elements. The figure graphs the time taken by a single append operation averaged over all operations for a given size, and averaged over the last one million operations for a given size. As expected, the time taken by append operations grows logarithmically with the size of the skip list, although for practical skip list sizes, the cost per append operation is virtually constant.
We also measure the performance of skip list proof extraction, in
Figure 9(b). The figure graphs the time
it takes to extract a precedence proof from a 100-million element
skip list for a given distance between the end-points of the proof
(the distance between elements ![]() and
and ![]() is
is ![]() elements). We
average over 1,000 uniformly random proof extractions per distance.
For small distances, different proofs fall within vastly different
disk blocks, making proof extraction performance heavily I/O bound.
For larger distances approaching the entire skip list size, random
proofs have many disk blocks in common, amortizing I/O overheads and
lowering the average cost.
elements). We
average over 1,000 uniformly random proof extractions per distance.
For small distances, different proofs fall within vastly different
disk blocks, making proof extraction performance heavily I/O bound.
For larger distances approaching the entire skip list size, random
proofs have many disk blocks in common, amortizing I/O overheads and
lowering the average cost.
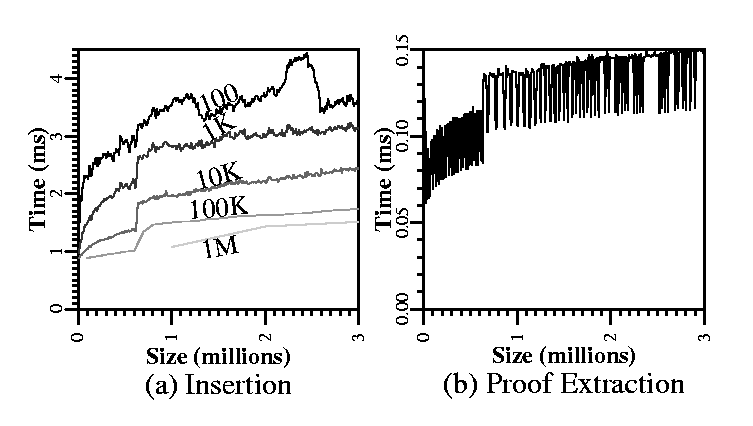 |
We continue by evaluating the performance characteristics of RBB-Trees. Figure 10 contains two graphs, one showing how insertion time grows with tree size (Figure 10(a)) and another showing how proof extraction time grows with tree size (Figure 10(b)).
Smaller snapshot sizes have two effects: more disk blocks for the same number of elements and more hashing. The number of disk blocks used is higher because some keys are replicated across more snapshots; the amount of hashing is higher since every new copy of a key node must have a new hash label calculated. The first effect is evidenced in Table 1, which shows the disk size of a three-million-key RBB-Tree with varying snapshot sizes. The second effect is evidenced in Figure 10(a), plotting insertion times for different snapshot sizes.
Proof extraction experiments consisted of 1,000 random searches for every size increment. This operation, which consists of a tree traversal from the root of the tree to a leaf, is not affected by snapshot size, but only by tree size (tree height, specifically). Neither the traversed logical ``shape'' of the tree, nor the distribution of keys into disk blocks are dependent on how frequently a tree snapshot is archived.
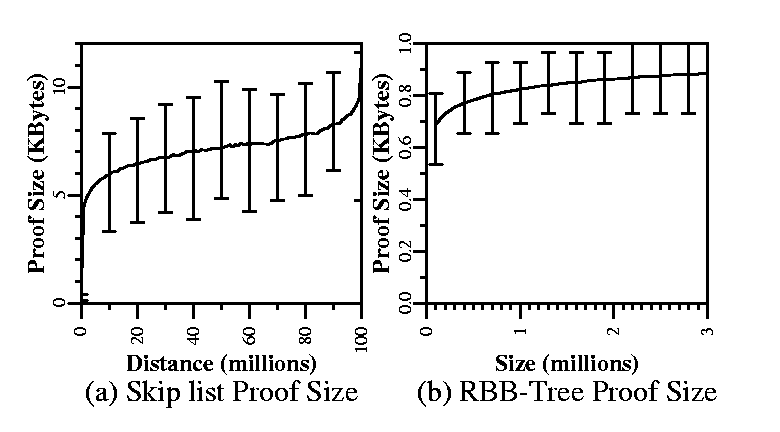 |
Finally, we graph proof sizes in skip lists (Figure 11(a)) and RBB-Trees (Figure 11(b)). Both graphs show proof sizes in KBytes, over 1,000 uniform random trials in a skip list of 100 million elements and an RBB-Tree of three million elements, respectively. The skip list curve starts out as a regular square logarithmic curve, except for large distances, close to the size of the entire list. We conjecture that the reason for this exception is that for random trials of distances close to the entire list size, all randomly chosen proofs are worst-case proofs, including every link of every level between source and destination, although we must explore this effect further. The RBB-Tree graph shows a regular logarithmic curve.
Although microbenchmarks can be helpful in understanding how the
basic blocks of Timeweave perform, they cannot give a complete
picture of how the system performs in action. For example, very
rarely does a Timeweave machine need to insert thousands of elements
into a skip list back-to-back. As a result, the disk block caching
available to batched insertions is not available for skip list usage
patterns exhibited by Timeweave. Similarly, most proof extractions
in timelines only span short distances; for one-second-long timeline
time steps with one entanglement process per peer every 10 minutes,
a Timeweave machine barely needs to traverse a distance of
![]() elements to extract a precedence proof, unlike the random
trials measured in Figure 9.
elements to extract a precedence proof, unlike the random
trials measured in Figure 9.
In this section we measure two performance metrics of a Timeweave machine in action: maintenance time and data transmitted. Timeweave maintenance consists of the different computations and data manipulations performed to verify, archive and acknowledge timeline threads. Transmitted data consist of new outgoing threads to the peers of the Timeweave machine and receipts for threads received from those peers.
We measure the change of these two metrics as the load of a
Timeweave machine changes. The load of a Timeweave machine is
roughly the number of incoming threads it has to handle per time
step. If we fix the duration of each time step to one second, and
the entanglement interval to 10 minutes (600 time steps), then a
load of 5 means that the entanglement service set consists of
![]() Timeweave machines and, as a result, every
Timeweave machine receives on average 5 threads per second.
Timeweave machines and, as a result, every
Timeweave machine receives on average 5 threads per second.
Figure 12(a) shows the time it takes a
single machine to perform Timeweave maintainance per one-second-long
time step. The almost perfectly linear rate at which maintenance
processing grows with the ratio of threads per time step indicates
that all-to-all entanglement can scale to large entangled service
sets only by limiting the entanglement frequency. However, for
reasonably large service sets, up to ![]() Timeweave machines for
10-minute entanglement, maintenance costs range between 2 and 8% of
the processing resources of a PC-grade server.
Timeweave machines for
10-minute entanglement, maintenance costs range between 2 and 8% of
the processing resources of a PC-grade server.
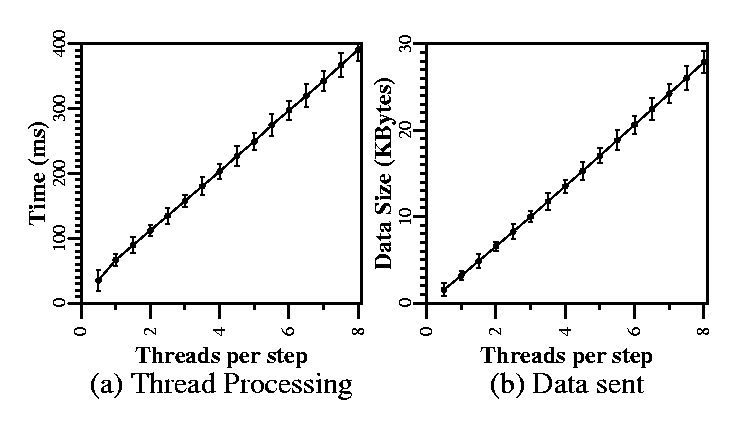 |
Figure 12(b) shows the amount of data sent per time step from a single Timeweave machine. Although the data rate itself is no cause for concern, the number of different destinations for secure transmissions could also limit how all-to-all entanglement scales. Again, for entangled service sets and entanglement intervals that do not exceed two or three threads per time step, Timeweave maintenance should not pose a problem to a low-end server with reasonable connectivity.
In this work we seek to extend the traditional idea of time stamping into the concept of a secure timeline, a tamper-evident historic record of the states through which a system passed in its lifetime. Secure timelines make it possible to reason about the temporal ordering of system states in a provable manner. We then proceed to define timeline entanglement, a technique for creating undeniable temporal orderings across mutually distrustful service domains. Finally, we design, describe the implementation of, and evaluate Timeweave, a prototype implementation of our timeline entanglement machinery, based on two novel authenticated data structures: append-only authenticated skip lists and disk-based, persistent authenticated search trees. Our measurements indicate that sizes of several hundred service domains can be efficiently entangled at a frequency of once every ten minutes using Timeweave.
Although our constructs preserve the correctness of temporal proofs,
they are not complete, since some events in a dishonest service
domain can be hidden from the timelines with which that domain
entangles (Section 4.3). We plan to alleviate this
shortcoming by employing a technique reminiscent of the
signed-messages solution to the traditional Byzantine Generals
problem [15]. Every time service ![]() sends a thread
to peer
sends a thread
to peer ![]() , it also piggybacks all the signed threads of other
services it has received and archived since the last time it sent a
thread to
, it also piggybacks all the signed threads of other
services it has received and archived since the last time it sent a
thread to ![]() . In such a manner, a service will be able to verify
that all members of the entangled service set have received the
same, unique timeline authenticator from every other service that it
has received and archived, verifying global historic integrity.
. In such a manner, a service will be able to verify
that all members of the entangled service set have received the
same, unique timeline authenticator from every other service that it
has received and archived, verifying global historic integrity.
We also hope to migrate away from the all-to-all entanglement model, by employing recently-developed, highly scalable overlay architectures such as CAN [22] and Chord [24]. In this way, a service only entangles its timeline with its immediate neighbors. Temporal proofs involving non-neighboring service domains use transitive temporal mapping, over the routing path in the overlay, perhaps choosing the route of least temporal loss.
Finally, we are working on a large scale distributed historic file system that enables the automatic maintenance of temporal orderings among file system operations across the entire system.
We thank Dan Boneh for suffering through the early stages of this work, as well as Hector Garcia-Molina and Neil Daswani for many helpful comments and pointed questions.
This work is supported by the Stanford Networking Research Center, by DARPA (contract N66001-00-C-8015) and by Sonera Corporation. Petros Maniatis is supported by a USENIX Scholar Fellowship.
|
This paper was originally published in the
Proceedings of the 11th USENIX Security Symposium,
August 5–9, 2002, San Francisco, CA, USA
Last changed: 19 June 2002 aw |
|