 Next:Implementation
Up:Contents
Previous:Algorithm
Properties
Next:Implementation
Up:Contents
Previous:Algorithm
Properties
The hard problem is guaranteeing that all non-faulty replicas agree on a total order for the execution of requests despite failures. We use a primary-backup mechanism to achieve this. In such a mechanism, replicas move through a succession of configurations called views. In a view one replica is the primary and the others are backups. We choose the primary of a view to be replica p such that p = v mod |R| where v is the view number and views are numbered consecutively.
The primary picks the ordering for execution of operations requested by clients. It does this by assigning a sequence number to each request. But the primary may be faulty. Therefore, the backups trigger view changes when it appears that the primary has failed to select a new primary. Viewstamped Replication [23] and Paxos [18] use a similar approach to tolerate benign faults.
To tolerate Byzantine faults, every step taken by a node in our system is based on obtaining a certificate. A certificate is a set of messages certifying some statement is correct and coming from different replicas. An example of a statement is: ``the result of the operation requested by a client is r''.
The size of the set of messages in a certificate is either f+1 or 2f+1, depending on the type of statement and step being taken. The correctness of our system depends on a certificate never containing more than f messages sent by faulty replicas. A certificate of size f+1 is sufficient to prove that the statement is correct because it contains at least one message from a non-faulty replica. A certificate of size 2f+1 ensures that it will also be possible to convince other replicas of the validity of the statement even when f replicas are faulty.
Our earlier algorithm [6] used the same basic ideas but it did not provide recovery. Recovery complicates the construction of certificates; if a replica collects messages for a certificate over a sufficiently long period of time it can end up with more than f messages from faulty replicas. We avoid this problem by introducing a notion of freshness; replicas reject messages that are not fresh. But this raises another problem: the view change protocol in [6] relied on the exchange of certificates between replicas and this may be impossible because some of the messages in a certificate may no longer be fresh. Section 4.5 describes a new view change protocol that solves this problem and also eliminates the need for expensive public-key cryptography.
To provide liveness with the new protocol, a replica must be able to fetch missing state that may be held by a single correct replica whose identity is not known. In this case, voting cannot be used to ensure correctness of the data being fetched and it is important to prevent a faulty replica from causing the transfer of unnecessary or corrupt data. Section 4.6 describes a mechanism to obtain missing messages and state that addresses these issues and that is efficient to enable frequent recoveries.
The sections below describe our algorithm. Sections 4.2 and 4.3, which explain normal-case request processing, are similar to what appeared in [6]. They are presented here for completeness and to highlight some subtle changes.
Some messages in the protocol contain a single MAC computed using UMAC32
[2]; we denote such a message as m
,
where i is the sender, j is the receiver and the MAC is computed
using kij. Other messages contain authenticators; we denote such
a message as
m
, where i is
the sender. An authenticator is a vector of MACs, one per replica j
(j
i), where the MAC in entry j is computed using kij. The receiver
of a message verifies its authenticity by checking the corresponding MAC
in the authenticator.
Replicas and clients refresh the session keys used to send messages
to them by sending new-key messages periodically (e.g., every minute).
The same mechanism is used to establish the initial session keys. The message
has the form NEW-KEY, i,..., {kji}
, ..., t
.
The message is signed by the secure co-processor (using the replica's private
key) and t is the value of its counter; the counter is incremented
by the co-processor and appended to the message every time it generates
a signature. (This prevents suppress-replay attacks [11].)
Each kji is the key replica j should use to authenticate messages
it sends to i in the future; kji is encrypted by j's public key,
so that only j can read it. Replicas use timestamp t to detect
spurious new-key messages: t must be larger than the timestamp of the
last new-key message received from i.
Each replica shares a single secret key with each client; this key is used for communication in both directions. The key is refreshed by the client periodically, using the new-key message. If a client neglects to do this within some system-defined period, a replica discards its current key for that client, which forces the client to refresh the key.
When a replica or client sends a new-key message, it discards all messages in its log that are not part of a complete certificate and it rejects any messages it receives in the future that are authenticated with old keys. This ensures that correct nodes only accept certificates with equally fresh messages, i.e., messages authenticated with keys created in the same refreshment phase.
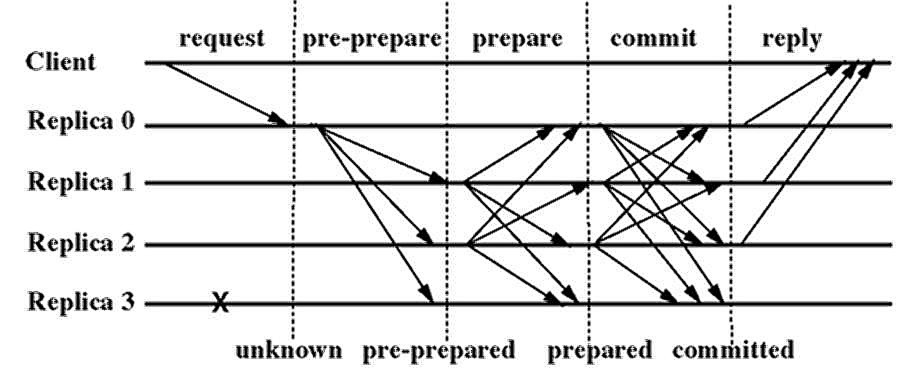
Each replica stores the service state, a log containing information about requests, and an integer denoting the replica's current view. The log records information about the request associated with each sequence number, including its status; the possibilities are: unknown (the initial status), pre-prepared, prepared, and committed. Figure 1 also shows the evolution of the request status as the protocol progresses. We describe how to truncate the log in Section 4.3.
A client c requests the execution of state machine operation o
by sending a REQUEST, o, t, c
message to the primary. Timestamp t is used to ensure exactly-once
semantics for the execution of client requests [6].
When the primary p receives a request m from a client, it assigns
a sequence number n to m. Then it multicasts a pre-prepare message
with the assignment to the backups, and marks m as pre-prepared with
sequence number n. The message has the form
PRE-PREPARE, v, n, d
, m
,
where v indicates the view in which the message is being sent, and
d is m's digest.
Like pre-prepares, the prepare and commit messages sent in the other phases also contain n and v. A replica only accepts one of these messages if it is in view v; it can verify the authenticity of the message; and n is between a low water mark, h, and a high water mark, H. The last condition is necessary to enable garbage collection and prevent a faulty primary from exhausting the space of sequence numbers by selecting a very large one. We discuss how h and H advance in Section 4.3.
A backup i accepts the pre-prepare message provided (in addition
to the conditions above): it has not accepted a pre-prepare for view v
and sequence number n containing a different digest; it can verify
the authenticity of m; and d is m's digest. If i accepts
the pre-prepare, it marks m as pre-prepared with sequence number n,
and enters the prepare phase by multicasting a
PREPARE, v, n, d, i
message to all other replicas.
When replica i has accepted a certificate with a pre-prepare message and 2f prepare messages for the same sequence number n and digest d (each from a different replica including itself), it marks the message as prepared. The protocol guarantees that other non-faulty replicas will either prepare the same request or will not prepare any request with sequence number n in view v.
Replica i multicasts
COMMIT, v, n, d, i
saying it prepared the request. This starts the commit phase. When a replica
has accepted a certificate with 2f+1 commit messages for the same sequence
number n and digest d from different replicas (including itself),
it marks the request as committed. The protocol guarantees that the request
is prepared with sequence number n in view v at f+1 or more non-faulty
replicas. This ensures information about committed requests is propagated
to new views.
Replica i executes the operation requested by the client when m is committed with sequence number n and the replica has executed all requests with lower sequence numbers. This ensures that all non-faulty replicas execute requests in the same order as required to provide safety.
After executing the requested operation, replicas send a reply to the
client c. The reply has the form
REPLY, v, t, c, i, r
where t is the timestamp of the corresponding request, i is the
replica number, and r is the result of executing the requested operation.
This message includes the current view number v so that clients can
track the current primary.
The client waits for a certificate with f+1 replies from different replicas and with the same t and r, before accepting the result r. This certificate ensures that the result is valid. If the client does not receive replies soon enough, it broadcasts the request to all replicas. If the request is not executed, the primary will eventually be suspected to be faulty by enough replicas to cause a view change and select a new primary.
We can determine this condition by extra communication, but to reduce cost we do the communication only when a request with a sequence number divisible by some constant K (e.g., 128) is executed. We will refer to the states produced by the execution of these requests as checkpoints.
When replica i produces a checkpoint, it multicasts a CHECKPOINT, n, d, i
message to the other replicas, where n is the sequence number of the
last request whose execution is reflected in the state and d is the digest
of the state. A replica maintains several logical copies of the service
state: the current state and some previous checkpoints. Section 4.6
describes how we manage checkpoints efficiently.
Each replica waits until it has a certificate containing 2f+1 valid checkpoint messages for sequence number n with the same digest d sent by different replicas (including possibly its own message). At this point, the checkpoint is said to be stable and the replica discards all entries in its log with sequence numbers less than or equal to n; it also discards all earlier checkpoints.
The checkpoint protocol is used to advance the low and high water marks (which limit what messages will be added to the log). The low-water mark h is equal to the sequence number of the last stable checkpoint and the high water mark is H = h + L, where L is the log size. The log size is obtained by multiplying K by a small constant factor (e.g., 2) that is big enough so that replicas do not stall waiting for a checkpoint to become stable.
Reboot. Recovery is proactive -- it starts periodically when the watchdog timer goes off. The recovery monitor saves the replica's state (the log and the service state) to disk. Then it reboots the system with correct code and restarts the replica from the saved state. The correctness of the operating system and service code is ensured by storing them in a read-only medium (e.g., the Seagate Cheetah 18LP disk can be write protected by physically closing a jumper switch). Rebooting restores the operating system data structures and removes any Trojan horses.
After this point, the replica's code is correct and it did not lose its state. The replica must retain its state and use it to process requests even while it is recovering. This is vital to ensure both safety and liveness in the common case when the recovering replica is not faulty; otherwise, recovery could cause the f+1st fault. But if the recovering replica was faulty, the state may be corrupt and the attacker may forge messages because it knows the MAC keys used to authenticate both incoming and outgoing messages. The rest of the recovery protocol solves these problems.
The recovering replica i starts by discarding the keys it shares with clients and it multicasts a new-key message to change the keys it uses to authenticate messages sent by the other replicas. This is important if i was faulty because otherwise the attacker could prevent a successful recovery by impersonating any client or replica.
Run estimation protocol. Next, i runs a simple protocol to estimate an upper bound, HM, on the high-water mark that it would have in its log if it were not faulty. It discards any entries with greater sequence numbers to bound the sequence number of corrupt entries in the log.
Estimation works as follows: i multicasts a QUERY-STABLE, i, r
message to all the other replicas, where r is a random nonce. When
replica j receives this message, it replies
REPLY-STABLE, c, p, i, r
where c and p are the sequence numbers of the last checkpoint and
the last request prepared at j respectively. i keeps retransmitting
the query message and processing replies; it keeps the minimum value of
c and the maximum value of p it received from each replica. It
also keeps its own values of c and p.
The recovering replica uses the responses to select HM as follows: HM = L + CM where L is the log size and CM is a value c received from replica j such that 2f replicas other than j reported values for c less than or equal to CM and f replicas other than j reported values of p greater than or equal to CM.
For safety, CM must be greater than any stable checkpoint so that i will not discard log entries when it is not faulty. This is insured because if a checkpoint is stable it will have been created by at least f+1 non-faulty replicas and it will have a sequence number less than or equal to any value of c that they propose. The test against p ensures that CM is close to a checkpoint at some non-faulty replica since at least one non-faulty replica reports a p not less than CM; this is important because it prevents a faulty replica from prolonging i's recovery. Estimation is live because there are 2f+1 non-faulty replicas and they only propose a value of c if the corresponding request committed and that implies that it prepared at at least f+1 correct replicas.
After this point i participates in the protocol as if it were not recovering but it will not send any messages above HM until it has a correct stable checkpoint with sequence number greater than or equal to HM.
Send recovery request. Next i sends a recovery request with
the form: REQUEST,
RECOVERY, HM
, t, i
This message is produced by the cryptographic co-processor and t is
the co-processor's counter to prevent replays. The other replicas reject
the request if it is a replay or if they accepted a recovery request from
i recently (where recently can be defined as half of the watchdog period).
This is important to prevent a denial-of-service attack where non-faulty
replicas are kept busy executing recovery requests.
The recovery request is treated like any other request: it is assigned
a sequence number nR and it goes through the usual three phases. But
when another replica executes the recovery request, it sends its own new-key
message. Replicas also send a new-key message when they fetch missing state
(see Section 4.6) and determine that
it reflects the execution of a new recovery request. This is important
because these keys are known to the attacker if the recovering replica
was faulty. By changing these keys, we bound the sequence number of messages
forged by the attacker that may be accepted by the other replicas -- they
are guaranteed not to accept forged messages with sequence numbers greater
than the maximum high water mark in the log when the recovery request executes,
i.e., HR = nR/K
K + L.
The reply to the recovery request includes the sequence number nR. Replica i uses the same protocol as the client to collect the correct reply to its recovery request but waits for 2f+1 replies. Then it computes its recovery point, H = max(HM, HR). It also computes a valid view (see Section 4.5); it retains its current view if there are f+1 replies for views greater than or equal to it, else it changes to the median of the views in the replies.
Check and fetch state. While i is recovering, it uses the state transfer mechanism discussed in Section 4.6 to determine what pages of the state are corrupt and to fetch pages that are out-of-date or corrupt.
Replica i is recovered when the checkpoint with sequence number H is stable. This ensures that any state other replicas relied on i to have is actually held by f+1 non-faulty replicas. Therefore if some other replica fails now, we can be sure the state of the system will not be lost. This is true because the estimation procedure run at the beginning of recovery ensures that while recovering i never sends bad messages for sequence numbers above the recovery point. Furthermore, the recovery request ensures that other replicas will not accept forged messages with sequence numbers greater than H.
Our protocol has the nice property that any replica knows that i has completed its recovery when checkpoint H is stable. This allows replicas to estimate the duration of i's recovery, which is useful to detect denial-of-service attacks that slow down recovery with low false positives.
The new view change protocol uses the techniques described in [6] to address liveness but uses a different approach to preserve safety. Our earlier approach relied on certificates that were valid indefinitely. In the new protocol, however, the fact that messages can become stale means that a replica cannot prove the validity of a certificate to others. Instead the new protocol relies on the group of replicas to validate each statement that some replica claims has a certificate. The rest of this section describes the new protocol.
Data structures. Replicas record information about what happened in earlier views. This information is maintained in two sets, the PSet and the QSet. A replica also stores the requests corresponding to the entries in these sets. These sets only contain information for sequence numbers between the current low and high water marks in the log; therefore only limited storage is required. The sets allow the view change protocol to work properly even when more than one view change occurs before the system is able to continue normal operation; the sets are usually empty while the system is running normally.
The PSet at replica i stores information about requests that have
prepared at i in previous views. Its entries are tuples n, d, v
meaning
that a request with digest d prepared at i with number n in view
v and no request prepared at i in a later view.
The QSet stores information about requests that have pre-prepared
at i in previous views (i.e., requests for which i has sent a pre-prepare
or prepare message). Its entries are tuples n, {...,
dk, vk
, ...}
meaning that for each k, vk is the latest view in which a request
pre-prepared with sequence number n and digest dk at i.
View-change messages. View changes are triggered when the current
primary is suspected to be faulty (e.g., when a request from a client is
not executed after some period of time; see [6]
for details). When a backup i suspects the primary for view v is
faulty, it enters view v+1 and multicasts a
VIEW-CHANGE, v+1, ls, C, P, Q, i
message to all replicas. Here ls is the sequence number of the latest
stable checkpoint known to i; C is a set of pairs with the sequence
number and digest of each checkpoint stored at i; and P and Q
are sets containing a tuple for every request that is prepared or pre-prepared,
respectively, at i. These sets are computed using the information in
the log, the PSet, and the QSet, as explained in Figure 2.
Once the view-change message has been sent, i stores P in PSet,
Q in QSet, and clears its log. The computation bounds the size of
each tuple in QSet; it retains only pairs corresponding to f+2 distinct
requests (corresponding to possibly f messages from faulty replicas,
one message from a good replica, and one special null message as explained
below). Therefore the amount of storage used is bounded.

View-change-ack messages. Replicas collect view-change messages
for v+1 and send acknowledgments for them to v+1's primary, p.
The acknowledgments have the form
VIEW-CHANGE-ACK, v+1, i, j, d
where i is the identifier of the sender, d is the digest of the view-change
message being acknowledged, and j is the replica that sent that view-change
message. These acknowledgments allow the primary to prove authenticity
of view-change messages sent by faulty replicas as explained later.
New-view message construction. The new primary p collects view-change and view-change-ack messages (including messages from itself). It stores view-change messages in a set S. It adds a view-change message received from replica i to S after receiving 2f-1 view-change-acks for i's view-change message from other replicas. Each entry in S is for a different replica. The new primary uses the information in S and the decision procedure sketched in Figure 3 to choose a checkpoint and a set of requests. This procedure runs each time the primary receives new information, e.g., when it adds a new message to S.

The primary starts by selecting the checkpoint that is going to be the starting state for request processing in the new view. It picks the checkpoint with the highest number h from the set of checkpoints that are known to be correct and that have numbers higher than the low water mark in the log of at least f+1 non-faulty replicas. The last condition is necessary for safety; it ensures that the ordering information for requests that committed with numbers higher than h is still available.
Next, the primary selects a request to pre-prepare in the new view for each sequence number between h and h+L (where L is the size of the log). For each number n that was assigned to some request m that committed in a previous view, the decision procedure selects m to pre-prepare in the new view with the same number. This ensures safety because no distinct request can commit with that number in the new view. For other numbers, the primary may pre-prepare a request that was in progress but had not yet committed, or it might select a special null request that goes through the protocol as a regular request but whose execution is a no-op.
We now argue informally that this procedure will select the correct value for each sequence number. If a request m committed at some non-faulty replica with number n, it prepared at at least f+1 non-faulty replicas and the view-change messages sent by those replicas will indicate that m prepared with number n. Any set of at least 2f+1 view-change messages for the new view must include a message from one of the non-faulty replicas that prepared m. Therefore, the primary for the new view will be unable to select a different request for number n because no other request will be able to satisfy conditions A1 or B (in Figure 3).
The primary will also be able to make the right decision eventually: condition A1 will be satisfied because there are 2f+1 non-faulty replicas and non-faulty replicas never prepare different requests for the same view and sequence number; A2 is also satisfied since a request that prepares at a non-faulty replica pre-prepares at at least f+1 non-faulty replicas. Condition A3 may not be satisfied initially, but the primary will eventually receive the request in a response to its status messages (discussed in Section 4.6). When a missing request arrives, this will trigger the decision procedure to run.
The decision procedure ends when the primary has selected a request
for each number. This takes O(L |R|3)
local steps in the worst case but the normal case is much faster because
most replicas propose identical values. After deciding, the primary multicasts
a new-view message to the other replicas with its decision. The new-view
message has the form
NEW-VIEW, v+1, V, X
.
Here, V contains a pair for each entry in S consisting of the identifier
of the sending replica and the digest of its view-change message, and X
identifies the checkpoint and request values selected.
New-view message processing. The primary updates its state to reflect the information in the new-view message. It records all requests in X as pre-prepared in view v+1 in its log. If it does not have the checkpoint with sequence number h it also initiates the protocol to fetch the missing state (see Section 4.6.2). In any case the primary does not accept any prepare or commit messages with sequence number less than or equal to h and does not send any pre-prepare message with such a sequence number.
The backups for view v+1 collect messages until they have a correct new-view message and a correct matching view-change message for each pair in V. If some replica changes its keys in the middle of a view change, it has to discard all the view-change protocol messages it already received with the old keys. The message retransmission mechanism causes the other replicas to re-send these messages using the new keys.
If a backup did not receive one of the view-change messages for some replica with a pair in V, the primary alone may be unable to prove that the message it received is authentic because it is not signed. The use of view-change-ack messages solves this problem. The primary only includes a pair for a view-change message in S after it collects 2f-1 matching view-change-ack messages from other replicas. This ensures that at least f+1 non-faulty replicas can vouch for the authenticity of every view-change message whose digest is in V. Therefore, if the original sender of a view-change is uncooperative, the primary retransmits that sender's view-change message and the non-faulty backups retransmit their view-change-acks. A backup can accept a view-change message whose authenticator is incorrect if it receives f view-change-acks that match the digest and identifier in V.
After obtaining the new-view message and the matching view-change messages, the backups check whether these messages support the decisions reported by the primary by carrying out the decision procedure in Figure 3. If they do not, the replicas move immediately to view v+2. Otherwise, they modify their state to account for the new information in a way similar to the primary. The only difference is that they multicast a prepare message for v+1 for each request they mark as pre-prepared. Thereafter, the protocol proceeds as described in Section 4.2.
The replicas use the status mechanism in Section 4.6 to request retransmission of missing requests as well as missing view-change, view-change acknowledgment, and new-view messages.
If a replica j is unable to validate a status message, it sends its last new-key message to i. Otherwise, j sends messages it sent in the past that i may be missing. For example, if i is in a view less than j's, j sends i its latest view-change message. In all cases, j authenticates messages it retransmits with the latest keys it received in a new-key message from i. This is important to ensure liveness with frequent key changes.
Clients retransmit requests to replicas until they receive enough replies. They measure response times to compute the retransmission timeout and use a randomized exponential backoff if they fail to receive a reply within the computed timeout.
It is important for the state transfer mechanism to be efficient because it is used to bring a replica up to date during recovery, and we perform proactive recoveries frequently. The key issues to achieving efficiency are reducing the amount of information transferred and reducing the burden imposed on replicas. This mechanism must also ensure that the transferred state is correct. We start by describing our data structures and then explain how they are used by the state transfer mechanism.
Data Structures. We use hierarchical state partitions to reduce the amount of information transferred. The root partition corresponds to the entire service state and each non-leaf partition is divided into s equal-sized, contiguous sub-partitions. We call leaf partitions pages and interior partitions meta-data. For example, the experiments described in Section 6 were run with a hierarchy with four levels, s equal to 256, and 4KB pages.
Each replica maintains one logical copy of the partition tree for each
checkpoint. The copy is created when the checkpoint is taken and it is
discarded when a later checkpoint becomes stable. The tree for a checkpoint
stores a tuple lm,d
for each meta-data partition and a tuple
lm,d,p
for each page. Here, lm is the sequence number of the checkpoint at the
end of the last checkpoint interval where the partition was modified, d
is the digest of the partition, and p is the value of the page.
The digests are computed efficiently as follows. For a page, d is obtained by applying the MD5 hash function [27] to the string obtained by concatenating the index of the page within the state, its value of lm, and p. For meta-data, d is obtained by applying MD5 to the string obtained by concatenating the index of the partition within its level, its value of lm, and the sum modulo a large integer of the digests of its sub-partitions. Thus, we apply AdHash [1] at each meta-data level. This construction has the advantage that the digests for a checkpoint can be obtained efficiently by updating the digests from the previous checkpoint incrementally.
The copies of the partition tree are logical because we use copy-on-write so that only copies of the tuples modified since the checkpoint was taken are stored. This reduces the space and time overheads for maintaining these checkpoints significantly.
Fetching State. The strategy to fetch state is to recurse down the hierarchy to determine which partitions are out of date. This reduces the amount of information about (both non-leaf and leaf) partitions that needs to be fetched.
A replica i multicasts FETCH, l, x, lc, c, k, i
to all replicas to obtain information for the partition with index x
in level l of the tree. Here, lc is the sequence number of the last
checkpoint i knows for the partition, and c is either -1 or it
specifies that i is seeking the value of the partition at sequence
number c from replica k.
When a replica i determines that it needs to initiate a state transfer, it multicasts a fetch message for the root partition with lc equal to its last checkpoint. The value of c is non-zero when i knows the correct digest of the partition information at checkpoint c, e.g., after a view change completes i knows the digest of the checkpoint that propagated to the new view but might not have it. i also creates a new (logical) copy of the tree to store the state it fetches and initializes a table LC in which it stores the number of the latest checkpoint reflected in the state of each partition in the new tree. Initially each entry in the table will contain lc.
If FETCH, l, x, lc, c, k, i
is received by the designated replier, k, and it has a checkpoint for
sequence number c, it sends back
META-DATA, c, l, x, P, k
where P is a set with a tuple
x', lm, d
for each sub-partition of (l, x)
with index x', digest d, and lm > lc. Since i knows the correct
digest for the partition value at checkpoint c, it can verify the correctness
of the reply without the need for voting or even authentication. This reduces
the burden imposed on other replicas.
The other replicas only reply to the fetch message if they have a stable checkpoint greater than lc and c. Their replies are similar to k's except that c is replaced by the sequence number of their stable checkpoint and the message contains a MAC. These replies are necessary to guarantee progress when replicas have discarded a specific checkpoint requested by i.
Replica i retransmits the fetch message (choosing a different k each time) until it receives a valid reply from some k or f+1 equally fresh responses with the same sub-partition values for the same sequence number cp (greater than lc and c). Then, it compares its digests for each sub-partition of (l, x) with those in the fetched information; it multicasts a fetch message for sub-partitions where there is a difference, and sets the value in LC to c (or cp) for the sub-partitions that are up to date. Since i learns the correct digest of each sub-partition at checkpoint c (or cp) it can use the optimized protocol to fetch them.
The protocol recurses down the tree until i sends fetch messages
for out-of-date pages. Pages are fetched like other partitions except that
meta-data replies contain the digest and last modification sequence number
for the page rather than sub-partitions, and the designated replier sends
back DATA, x, p
.
Here, x is
the page index and p is the page value. The protocol imposes little
overhead on other replicas; only one replica replies with the full page
and it does not even need to compute a MAC for the message since i
can verify the reply using the digest it already knows.
When i obtains the new value for a page, it updates the state of the page, its digest, the value of the last modification sequence number, and the value corresponding to the page in LC. Then, the protocol goes up to its parent and fetches another missing sibling. After fetching all the siblings, it checks if the parent partition is consistent. A partition is consistent up to sequence number c if c is the minimum of all the sequence numbers in LC for its sub-partitions, and c is greater than or equal to the maximum of the last modification sequence numbers in its sub-partitions. If the parent partition is not consistent, the protocol sends another fetch for the partition. Otherwise, the protocol goes up again to its parent and fetches missing siblings.
The protocol ends when it visits the root partition and determines that it is consistent for some sequence number c. Then the replica can start processing requests with sequence numbers greater than c.
Since state transfer happens concurrently with request execution at other replicas and other replicas are free to garbage collect checkpoints, it may take some time for a replica to complete the protocol, e.g., each time it fetches a missing partition, it receives information about yet a later modification. This is unlikely to be a problem in practice (this intuition is confirmed by our experimental results). Furthermore, if the replica fetching the state ever is actually needed because others have failed, the system will wait for it to catch up.
The message authentication mechanism from Section 4.1 ensures non-faulty nodes only accept certificates with messages generated within an interval of size at most 2Tk.1 The bound on the number of faults within Tv ensures there are never more than f faulty replicas within any interval of size at most 2Tk. Therefore, safety and liveness are provided because non-faulty nodes never accept certificates with more than f bad messages.
We have little control over the value of Tv because Tr may be increased by a denial-of-service attack, but we have good control over Tk and the maximum time between watchdog timeouts, Tw, because their values are determined by timer rates, which are quite stable. Setting these timeout values involves a tradeoff between security and performance: small values improve security by reducing the window of vulnerability but degrade performance by causing more frequent recoveries and key changes. Section 6 analyzes this tradeoff.
The value of Tw should be set based on Rn, the time it takes
to recover a non-faulty replica under normal load conditions. There is
no point in recovering a replica when its previous recovery has not yet
finished; and we stagger the recoveries so that no more than f replicas
are recovering at once, since otherwise service could be interrupted even
without an attack. Therefore, we set Tw = 4 s
Rn
Here, the factor 4 accounts for the staggered recovery of 3f+1 replicas
f at a time, and s is a safety factor to account for benign overload
conditions (i.e., no attack).
Another issue is the bound f on the number of faults. Our replication technique is not useful if there is a strong positive correlation between the failure probabilities of the replicas; the probability of exceeding the bound may not be lower than the probability of a single fault in this case. Therefore, it is important to take steps to increase diversity. One possibility is to have diversity in the execution environment: the replicas can be administered by different people; they can be in different geographic locations; and they can have different configurations (e.g., run different combinations of services, or run schedulers with different parameters). This improves resilience to several types of faults, for example, attacks involving physical access to the replicas, administrator attacks or mistakes, attacks that exploit weaknesses in other services, and software bugs due to race conditions. Another possibility is to have software diversity; replicas can run different operating systems and different implementations of the service code. There are several independent implementations available for operating systems and important services (e.g. file systems, data bases, and WWW servers). This improves resilience to software bugs and attacks that exploit software bugs.
Even without taking any steps to increase diversity, our proactive recovery technique increases resilience to nondeterministic software bugs, to software bugs due to aging (e.g., memory leaks), and to attacks that take more time than Tv to succeed. It is possible to improve security further by exploiting software diversity across recoveries. One possibility is to restrict the service interface at a replica after its state is found to be corrupt. Another potential approach is to use obfuscation and randomization techniques [7,9] to produce a new version of the software each time a replica is recovered. These techniques are not very resilient to attacks but they can be very effective when combined with proactive recovery because the attacker has a bounded time to break them.
1
It would be Tk except that during view changes replicas may accept messages
that are claimed authentic by f+1 replicas without directly checking
their authentication token.
Next:Implementation Up:Contents Previous:Algorithm
Properties
Miguel Castro and Barbara Liskov, "Proactive Recovery in a Byzantine-Fault-Tolerant System", in Proceedings of the Fourth Symposium on Operating Systems
Design and Implementation, San Diego, USA, October 2000.