Check out the new USENIX Web site.

[


Network Imprecision: A New Consistency Metric for Scalable Monitoring


Navendu Jain$ ^\dagger$ , Prince Mahajan$ ^\star$ , Dmitry Kit$ ^\star$ , Praveen Yalagandula$ ^\ddagger$ , Mike Dahlin$ ^\star$ , and Yin Zhang$ ^\star$
$ ^\dagger$ Microsoft Research $ ^\star$ The University of Texas at Austin $ ^\ddagger$ HP Labs



]

Abstract:

This paper introduces a new consistency metric, Network Imprecision (NI), to address a central challenge in large-scale monitoring systems: safeguarding accuracy despite node and network failures. To implement NI, an overlay that monitors a set of attributes also monitors its own state so that queries return not only attribute values but also information about the stability of the overlay--the number of nodes whose recent updates may be missing and the number of nodes whose inputs may be double counted due to overlay reconfigurations. When NI indicates that the network is stable, query results are guaranteed to reflect the true state of the system. But when the network is unstable, NI puts applications on notice that query results should not be trusted, allowing them to take corrective action such as filtering out inconsistent results. To scalably implement NI's introspection, our prototype introduces a key optimization, dual-tree prefix aggregation, which exploits overlay symmetry to reduce overheads by more than an order of magnitude. Evaluation of three monitoring applications demonstrates that NI flags inaccurate results while incurring low overheads, and monitoring applications that use NI to select good information can improve their accuracy by up to an order of magnitude.


1 Introduction

Scalable system monitoring is a fundamental abstraction for large-scale networked systems. It enables operators and end-users to characterize system behavior, from identifying normal conditions to detecting unexpected or undesirable events--attacks, configuration mistakes, security vulnerabilities, CPU overload, or memory leaks--before serious harm is done. Therefore, it is a critical part of infrastructures ranging from network monitoring [30,32,10,23,54], financial applications [3], resource scheduling [27,53], efficient multicast [51], sensor networks [25,27,53], storage systems [50], and bandwidth provisioning [15], that potentially track thousands or millions of dynamic attributes (e.g., per-flow or per-object state) spanning thousands of nodes.

Three techniques are important for scalability in monitoring systems: (1) hierarchical aggregation [51,30,53,27] allows a node to access detailed views of nearby information and summary views of global information, (2) arithmetic filtering [30,31,36,42,56] caches recent reports and only transmits new information if it differs by some numeric threshold (e.g., $ \pm$ 10%) from the cached report, and (3) temporal batching [32,36,42,51] combines multiple updates that arrive near one another in time into a single message. Each of these techniques can reduce monitoring overheads by an order of magnitude or more [30,31,53,42].

As important as these techniques are for scalability, they interact badly with node and network failures: a monitoring system that uses any of these techniques risks reporting highly inaccurate results.

These effects can be significant. For example, in an 18-hour interval for a PlanetLab monitoring application, we observed that more than half of all reports differed from the ground truth at the inputs by more than 30%. These best effort results are clearly unacceptable for many applications.

To address these challenges, we introduce Network Imprecision (NI), a new consistency metric suitable for large-scale monitoring systems with unreliable nodes or networks. Intuitively, NI represents a ``stability flag'' indicating whether the underlying network is stable or not. More specifically, with each query result, NI provides (1) the number of nodes whose recent updates may not be reflected in the current answer, (2) the number of nodes whose inputs may be double counted due to overlay reconfiguration, and (3) the total number of nodes in the system. A query result with no unreachable or double counted nodes is guaranteed to reflect reality, but an answer with many of either indicates a low system confidence in that query result--the network is unstable, hence the result should not be trusted.

We argue that NI's introspection on overlay state is the right abstraction for a monitoring system to provide to monitoring applications. On one hand, traditional data consistency algorithms [56] must block reads or updates during partitions to enforce limits on inconsistency [19]. However, in distributed monitoring, (1) updates reflect external events that are not under the system's control so cannot be blocked and (2) reads depend on inputs at many nodes, so blocking reads when any sensor is unreachable would inflict unacceptable unavailability. On the other hand, ``reasoning under uncertainty'' techniques [48] that try to automatically quantify the impact of disruptions on individual attributes are expensive because they require per-attribute computations. Further, these techniques require domain knowledge thereby limiting flexibility for multi-attribute monitoring systems [53,51,42], or use statistical models which are likely to be ineffective for detecting unusual events like network anomalies [26]. Even for applications where such application-specific or statistical techniques are appropriate, NI provides a useful signal telling applications when these techniques should be invoked.

NI allows us to construct PRISM (PRecision Integrated Scalable Monitoring), a new monitoring system that maximizes scalability via arithmetic filtering, temporal batching, and hierarchy. A key challenge in PRISM is implementing NI efficiently. First, because a given failure has different effects on different aggregation trees embedded in PRISM's scalable DHT, the NI reported with an attribute must be specific to that attribute's tree. Second, detecting missing updates due to failures, delays, and reconfigurations requires frequent active probing of paths within a tree. To provide a topology-aware implementation of NI that scales to tens of thousands of nodes and millions of attributes, PRISM introduces a novel dual-tree prefix aggregation construct that exploits symmetry in its DHT-based aggregation topology to reduce the per-node overhead of tracking the $ n$ distinct NI values relevant to $ n$ aggregation trees in an $ n$ -node DHT from $ O(n)$ to $ O(\log{n})$ messages per time unit. For a 10K-node system, dual tree prefix aggregation reduces the per node cost of tracking NI from a prohibitive 1000 messages per second to about 7 messages per second.

Our NI design separates mechanism from policy and allows applications to use any desired technique to quantify and minimize the impact of disruptions on system reports. For example, in PRISM, monitoring applications use NI to safeguard accuracy by (1) inferring an approximate confidence interval for the number of sensor inputs contributing to a query result, (2) differentiating between correct and erroneous results based on their NI, or (3) correcting distorted results by applying redundancy techniques and then using NI to automatically select the best results. By using NI metrics to filter out inconsistent results and automatically select the best of four redundant aggregation results, we observe a reduction in the worst-case inaccuracy by up to an order of magnitude.

This paper makes five contributions. First, we present Network Imprecision, a new consistency metric that characterizes the impact of network instability on query results. Second, we demonstrate how different applications can leverage NI to detect distorted results and take corrective action.Third, we provide a scalable implementation of NI for DHT overlays via dual-tree prefix aggregation. Fourth, our evaluation demonstrates that NI is vital for enabling scalable aggregation: a system that ignores NI can often silently report arbitrarily incorrect results. Finally, we demonstrate how a distributed monitoring system can both maximize scalability by combining hierarchy, arithmetic filtering, and temporal batching and also safeguard accuracy by incorporating NI.


2 Scalability vs. correctness

Figure 1: The aggregation tree for key 000 in an eight node system. Also shown are the aggregate values for a simple SUM() aggregation function.
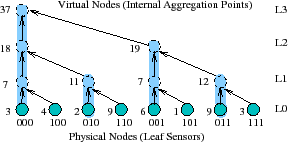\begin{figure}\begin{center} \epsfig{figure=figures/DHTEx111.eps,width=2.5in}\end{center}\vspace{-.04in} \end{figure}

As discussed in Section 1, large-scale monitoring systems face two key challenges to safeguarding result accuracy. First, node failures, network disruptions, and topology reconfigurations imperil accuracy of monitoring results. Second, common scalability techniques--hierarchical aggregation [5,44,47,53], arithmetic filtering [30,31,36,42,51,56,38], and temporal batching [32,56,36,14]--make the problem worse. In particular, although each technique significantly enhances scalability, each also increases the risk that disruptions will cause the system to report incorrect results.

For concreteness, we describe PRISM's implementation of these techniques although the challenges in safeguarding accuracy are applicable to any monitoring system that operates under node and network failures. We compute a SUM aggregate for all the examples in this section.

Hierarchical aggregation. Many monitoring systems use hierarchical aggregation [51,47] or DHT-based hierarchical aggregation [5,44,53,39] that defines a tree spanning all nodes in the system. As Figure 1 illustrates, in PRISM, each physical node is a leaf and each subtree represents a logical group of nodes; logical groups can correspond to administrative domains (e.g., department or university) or groups of nodes within a domain (e.g., a /$ 28$ IPv4 subnet with $ 14$ hosts in the CS department) [22,53]. An internal non-leaf node, which we call a virtual node, is emulated by a physical leaf node of the subtree rooted at the virtual node.

PRISM leverages DHTs [44,46,49] to construct a forest of aggregation trees and maps different attributes to different trees for scalability. DHT systems assign a long (e.g., 160 bits), random ID to each node and define a routing algorithm to send a request for ID $ i$ to a node $ root_i$ such that the union of paths from all nodes forms a tree DHTtree$ _i$ rooted at the node root$ _i$ . By aggregating an attribute with ID $ i$ = hash(attribute) along the aggregation tree corresponding to DHTtree$ _i$ , different attributes are load balanced across different trees. This approach can provide aggregation that scales to large numbers of nodes and attributes [53,47,44,5].

Figure 2: Dynamically-constructed aggregation hierarchies raise two challenges for guaranteeing the accuracy of reported results: the failure amplification effect and double counting caused by reconfiguration.
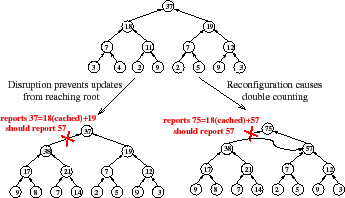\begin{figure}\centerline{\epsfig{figure=figures/hier-ambiguity.eps,width=3.0in}} \end{figure}

Unfortunately, as Figure 2 illustrates, hierarchical aggregation imperils correctness in two ways. First, a failure of a single node or network path can prevent updates from a large collection of leaves from reaching the root, amplifying the effect of the failure [41]. Second, node and network failures can trigger DHT reconfigurations that move a subtree from one attachment point to another, causing the subtree's inputs to be double counted by the aggregation function for some period of time.

Arithmetic Imprecision (AI). Arithmetic imprecision deterministically bounds the difference between the reported aggregate value and the true value. In PRISM, each aggregation function reports a bounded numerical range {$ V_{min}$ , $ V_{max}$ } that contains the true aggregate value $ V$ i.e., $ V_{min} \leq V \leq V_{max}$ .

Allowing such arithmetic imprecision enables arithmetic filtering: a subtree need not transmit an update unless the update drives the aggregate value outside the range it last reported to its parent; a parent caches last reported ranges of its children as soft state. Numerous systems have found that allowing small amounts of arithmetic imprecision can greatly reduce overheads [30,31,36,42,51,56].

Figure 3: Arithmetic filtering makes it difficult to determine if a subtree's silence is because the subtree has nothing to report or is unreachable.
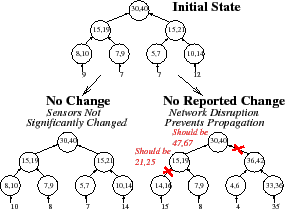\begin{figure}\centerline{\epsfig{figure=figures/figure3.eps,width=2.5in}} \end{figure}

Unfortunately, as Figure 3 illustrates, arithmetic filtering raises a challenge for correctness: if a subtree is silent, it is difficult for the system to distinguish between two cases. Either the subtree has sent no updates because the inputs have not significantly changed from the cached values or the inputs have significantly changed but the subtree is unable to transmit its report.

Temporal Imprecision (TI). Temporal imprecision bounds the delay from when an event occurs until it is reported. In PRISM, each attribute has a TI guarantee, and to meet this bound the system must ensure that updates propagate from the leaves to the root in the allotted time.

Figure 4: Temporal batching allows leaf sensors to condense a series of updates into a periodic report and allows internal nodes to combine updates from different subtrees before transmitting them further.
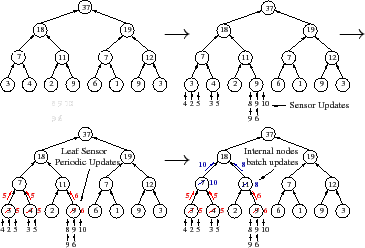\begin{figure}\begin{center} \begin{tabular}{cccc} \epsfig{figure=figures/figure... ...figures/figure4d.eps,width=1.45in} & \\ \end{tabular}\end{center} \end{figure}

As Figure 4 illustrates, TI allows PRISM to use temporal batching: a set of updates at a leaf sensor are condensed into a periodic report or a set of updates that arrive at an internal node over a time interval are combined before being sent further up the tree. Note that arithmetic filtering and temporal batching are complementary: a batched update need only be sent if the combined update drives a subtree's attribute value out of the range previously reported up the tree.

Of course, an attribute's TI guarantee can only be ensured if there is a good path from each leaf to the root. A good path is a path whose processing and propagation times fall within some pre-specified delay budget. Unfortunately, failures, overload, or network congestion can cause a path to no longer be good and prevent the system from meeting its TI guarantees. Furthermore, when a system batches a large group of updates together, a short network or node failure can cause a large error. For example, suppose a system is enforcing TI=60s for an attribute, and suppose that an aggregation node near the root has collected 59 seconds worth of updates from its descendents but then loses its connection to the root for a few seconds. That short disruption can cause the system to violate its TI guarantees for a large number of updates.


3 NI Abstraction and Application

To cope with the sources of error just described, we introduce a new consistency metric, Network Imprecision (NI), that addresses the needs of large-scale monitoring systems in environments where networks or nodes can fail.

This section defines NI and argues that it is the right abstraction for a monitoring system to provide to monitoring applications. The discussions in this section assume that NI is provided by an oracle. Section 4 describes how to compute the NI metrics accurately and efficiently.

Figure 5: The evolution of $ N_{reachable}$ , $ N_{all}$ , and $ N_{dup}$ during failures and reconfigurations. The values in the center of each circle illustrate an example SUM aggregate. The vertical bars show the virtual nodes corresponding to a given physical leaf node.
\begin{figure*}\begin{center} \begin{tabular}{ccccc} \epsfig{figure=figures/NI-e... ...ion & (d) Reconfig 1 & (e) Reconfig 2\\ \end{tabular}\end{center} \end{figure*}


1 NI metrics

The definition of NI is driven by four fundamental properties of large-scale monitoring systems. First, updates reflect real-world events that are outside of the system's control. Second, updates can occur at large numbers of sensor nodes. Third, systems may support monitoring of large numbers of attributes. Fourth, different applications are affected by and may react to missing updates in different ways.

The first two properties suggest that traditional data consistency algorithms that enforce guarantees like causal consistency [33] or sequential consistency [34] or linearizability [24] are not appropriate for large-scale monitoring systems. To enforce limits on inconsistency, traditional consistency algorithms must block reads or writes during partitions [19]. However, in large-scale monitoring systems (1) updates cannot be blocked because they reflect external events that are not under the system's control and (2) reads depend on inputs at many nodes, so blocking reads when any sensor is unreachable will result in unacceptable availability.

We therefore cast NI as a monitoring system's introspection on its own stability. Rather than attempt to enforce limits on the inconsistency of data items, a monitoring overlay uses introspection on its current state to produce an NI value that exposes the extent to which system disruptions may affect results.

In its simplest form, NI could be provided as a simple stability flag. If the system is stable (all nodes are up, all network paths are available, and all updates are propagating within the delays specified by the system's temporal imprecision guarantees), then an application knows that it can trust the monitoring system's outputs. Conversely, if the monitoring system detects that any of these conditions is violated, it could simply flag its outputs as suspect, warning applications that some sensors' updates may not be reflected in the current outputs.

Since large systems may seldom be completely stable and in order to allow different applications sufficient flexibility to handle system disruptions, instead of an all-or-nothing stability flag, our implementation of the NI abstraction quantifies the scope of system disruptions. In particular, we provide three metrics: $ N_{all}$ , $ N_{reachable}$ , and $ N_{dup}$ .

These three metrics characterize the consistency of a query result. If $ N_{reachable}$ $ =$ $ N_{all}$ and $ N_{dup}$ $ =$ 0 , then query results are guaranteed to meet the AI and TI bounds specified by the system. If $ N_{reachable}$ is close to $ N_{all}$ and $ N_{dup}$ is low, the results reflect most inputs and are likely to be useful for many applications. Conversely, query answers with high values of $ N_{all}$ $ -$ $ N_{reachable}$ or $ N_{dup}$ suggest that the network is unstable and the results should not be trusted.

Mechanism vs. policy. This formulation of NI explicitly separates the mechanism for network introspection of a monitoring system from application-specific policy for detecting and minimizing the effects of failures, delays, or reconfigurations on query results. Although it is appealing to imagine a system that not only reports how a disruption affects the overlay but also how the disruption affects each monitored attribute, we believe that NI provides the right division of labor between the monitoring system and monitoring applications for three reasons.

First, the impact of omitted or duplicated updates is highly application-dependent, depending on the aggregation function (e.g., some aggregation functions are insensitive to duplicates [12]), the variability of the sensor inputs (e.g., when inputs change slowly, using a cached update for longer than desired may have a modest impact), the nature of the application (e.g., an application that attempts to detect unusual events like network anomalies may reap little value from using statistical techniques for estimating the state of unreachable sensors), and application requirements (e.g., some applications may value availability over correctness and live with best effort answers while others may prefer not to act when the accuracy of information is suspect).

Second, even if it were possible to always estimate the impact of disruptions on applications, hard-wiring the system to do such per-attribute work would impose significant overheads compared to monitoring the status of the overlay.

Third, as we discuss in Section 3.3, there are a broad range of techniques that applications can use to cope with disruptions, and our definition of NI allows each application to select the most appropriate technique.


2 Example

Here, we illustrate how NI's three metrics characterize system state using a simple example.

Consider the aggregation tree across 5 physical nodes in Figure 5(a). For simplicity, we compute a SUM aggregate under an AI filtering budget of zero (i.e., update propagation is suppressed if the value of an attribute has not changed), and we assume a TI guarantee of $ TI_{limit}$ = 30 seconds (i.e., the system promises a maximum staleness of 30 seconds). Finally, to avoid spurious garbage collection/reconstruction of per-attribute state, the underlying DHT reconfigures its topology if a path is down for a long timeout (e.g., a few minutes), and internal nodes cache inputs from their children as soft state for slightly longer than that amount of time.

Initially, (a) the system is stable; the root reports the correct aggregate value of 25 with $ N_{all}$ $ =$ $ N_{reachable}$ $ =$ 5 and $ N_{dup}$ $ =$ 0 indicating that all nodes' recent inputs are reflected in the aggregate result with no duplication.

Then, (b) the input value changes from 7 to 6 at a leaf node, but before sending that update, the node gets disconnected from its parent. Because of soft state caching, the failed node's old input is still reflected in the SUM aggregate, but recent changes at that sensor are not; the root reports 25 but the correct answer is 24. As (b) shows, NI exposes this inconsistency to the application by changing $ N_{reachable}$ to 4 within $ TI_{limit}$ = 30 seconds of the disruption, indicating that the reported result is based on stale information from at most one node.

Next, we show how NI exposes the failure amplification effect. In (c), a single node failure disconnects the entire subtree rooted at that node. NI reveals this major disruption by reducing $ N_{reachable}$ to 2 since only two leaves retain a good path to the root. The root still reports 25 but the correct answer (i.e., what an oracle would compute using the live sensors' values as inputs) is 18. Since only 2 of 5 nodes are reachable, this report is suspect. The application can either discard it or take corrective actions such as those discussed in Section 3.3.

NI also exposes the effects of overlay reconfiguration. After a timeout, (d) the affected leaves switch to new parents; NI exposes this change by increasing $ N_{reachable}$ to 4. But since the nodes' old values may still be cached, $ N_{dup}$ increases to 2 indicating that two nodes' inputs are double counted in the root's answer of 34.

Finally, NI reveals when the system has restabilized. In (e), the system again reaches a stable state--the soft state expires, $ N_{dup}$ falls to zero, $ N_{all}$ becomes equal to $ N_{reachable}$ of 4, and the root reports the correct aggregate value of 18.


3 Using NI

As noted above, NI explicitly separates the problem of characterizing the state of the monitoring system from the problem of assessing how disruptions affect applications. The NI abstraction is nonetheless powerful--it supports a broad range of techniques for coping with network and node disruptions. We first describe four standard techniques we have implemented: (1) flag inconsistent answers, (2) choose the best of several answers, (3) on-demand reaggregation when inconsistency is high, and (4) probing to determine the numerical contribution of duplicate or stale inputs. We then briefly sketch other ways applications can use NI.

Filtering or flagging inconsistent answers. PRISM's first standard technique is to manage the trade-off between consistency and availability [19] by sacrificing availability: applications report an exception rather than returning an answer when the fraction of unreachable or duplicate inputs exceeds a threshold. Alternatively, applications can maximize availability by always returning an answer based on the best available information but flagging that answer's quality as high, medium, or low depending on the number of unreachable or duplicated inputs.

Redundant aggregation. PRISM can aggregate an attribute using $ k$ different keys so that one of the keys is likely to find a route around the disruption. Since each key is aggregated using a different tree, each has a different NI associated with it, and the application chooses the result associated with the key that has the best NI. In Section 6, we show that using a small value of $ k$ ($ k=$ 4) reduces the worst-case inaccuracy by nearly a factor of five.

On-demand reaggregation. Given a signal that current results may be affected by significant disruptions, PRISM allows applications to trigger a full on-demand reaggregation to gather current reports (without AI caching or TI buffering) from all available inputs. In particular, if an application receives an answer with unacceptably high fraction of unreachable or duplicated inputs, it issues a probe to force all nodes in the aggregation tree to discard their cached data for the attribute and to recompute the result using the current value at all reachable leaf inputs.

Determine $ V_{dup}$ or $ V_{stale}$ . When $ N_{dup}$ or $ N_{all} - N_{reachable}$ is high, an application knows that many inputs may be double counted or stale. An application can gain additional information about how the network disruption affects a specific attribute by computing $ V_{dup}$ or $ V_{stale}$ for that attribute. $ V_{dup}$ is the aggregate function applied to all inputs that indicate that they may also be counted in another subtree; for example in Figure 5(d), $ V_{dup}$ is 9 from the two nodes on the left that have taken new parents before they are certain that their old parent's soft state has been reclaimed. Similarly, $ V_{stale}$ is the aggregate function applied across cached values from unreachable children; in Figure 5(c) $ V_{stale}$ is 16, indicating that 16/25 of the sum value comes from nodes that are currently unreachable.

Since per-attribute $ V_{dup}$ and $ V_{stale}$ provide more information than the NI metrics, which merely characterize the state of the topology without reference to the aggregation functions or their values, it is natural to ask: Why not always provide $ V_{dup}$ and $ V_{stale}$ and dispense with the NI metrics entirely? As we will show in Section 4, the NI metrics can be computed efficiently. Conversely, the attribute-specific $ V_{dup}$ and $ V_{stale}$ metrics must be computed and actively maintained on a per-attribute basis, making them too expensive for monitoring a large number of attributes. Given the range of techniques that can make use of the much cheaper NI metrics, PRISM provides NI as a general mechanism but allows applications that require (and are willing to pay for) the more detailed $ V_{dup}$ and $ V_{stale}$ information to do so.

Other techniques. For other monitoring applications, it may be useful to apply other domain-specific or application-specific techniques. Examples include

These examples are illustrative but not comprehensive. Armed with information about the likely quality of a given answer, applications can take a wide range of approaches to protect themselves from disruptions.


4 Computing NI metrics

The three NI metrics are simple, and implementing them initially seems straightforward: $ N_{all}$ , $ N_{reachable}$ , and $ N_{dup}$ are each conceptually aggregates of counts across nodes, which appear to be easy to compute using PRISM's standard aggregation features. However, this simple picture is complicated by two requirements on our solution:

  1. Correctness despite reconfigurations. PRISM must cope with reconfiguration of dynamically constructed aggregation trees while still guaranteeing the invariants that (a) query results reflect current (to the limits of each attribute's TI bounds) inputs from at least $ N_{reachable}$ nodes and (b) query results reflect at most $ N_{dup}$ duplicate inputs due to topology reconfigurations.

  2. Scalability. PRISM must scale to large numbers of nodes despite (a) the need for active probing to measure liveness between each parent-child pair and (b) the need to compute distinct NI values for each of the distinct aggregation trees in the underlying DHT forest. Naive implementations of NI would incur excessive monitoring overhead as we show in Section 4.3.

In the rest of this section, we first provide a simple algorithm for computing $ N_{all}$ and $ N_{reachable}$ for a single, static tree. Then, in Section 4.2, we explain how PRISM computes $ N_{dup}$ to account for dynamically changing aggregation topologies. Later, in Section 4.3 we describe how to scale the approach to a large number of distinct trees constructed by PRISM's DHT framework.


1 Single tree, static topology

This section considers calculating $ N_{all}$ and $ N_{reachable}$ for a single, static-topology aggregation tree.

$ N_{all}$ is simply a count of all nodes in the system, which serves as a baseline for evaluating $ N_{reachable}$ and $ N_{dup}$ . $ N_{all}$ is easily computed using PRISM's aggregation abstraction. Each leaf node inserts 1 to the $ N_{all}$ aggregate, which has SUM as its aggregation function.

$ N_{reachable}$ for a subtree is a count of the number of leaves that have a good path to the root of the subtree, where a good path is a path whose processing and network propagation times currently fall within the system's smallest supported TI bound $ TI_{min}$ . The difference $ N_{all}$ $ -$ $ N_{reachable}$ thus represents the number of nodes whose inputs may fail to meet the system's tightest supported staleness bound; we will discuss what happens for attributes with TI bounds larger than $ TI_{min}$ momentarily.

Nodes compute $ N_{reachable}$ in two steps:

  1. Basic aggregation: PRISM creates a SUM aggregate and each leaf inserts local value of 1. The root of the tree then gets a count of all nodes.

  2. Aggressive pruning: $ N_{reachable}$ must immediately change if the connection to a subtree is no longer a good path. Therefore, each internal node periodically probes each of its children. If a child $ c$ is not responsive, the node removes the subtree $ c$ 's contribution from the $ N_{reachable}$ aggregate and immediately sends the new value up towards the root of the $ N_{reachable}$ aggregation tree.

To ensure that $ N_{reachable}$ is a lower bound on the number of nodes whose inputs meet their TI bounds, PRISM processes these probes using the same data path in the tree as the standard aggregation processing: a child sends a probe reply only after sending all queued aggregate updates and the parent processes the reply only after processing all previous aggregate updates. As a result, if reliable, FIFO network channels are used, then our algorithm introduces no false negatives: if probes are processed within their timeouts, then so are all aggregate updates. Note that our prototype uses FreePastry [46], which sends updates via unreliable channels, and our experiments in Section 6 do detect a small number of false negatives where a responsive node is counted as reachable even though some recent updates were lost by the network. We also expect few false positives: since probes and updates travel the same path, something that delays processing of probes will likely also affect at least some other attributes.

Supporting temporal batching. If an attribute's TI bound is relaxed to $ TI_{attr}$ $ >$ $ TI_{min}$ , PRISM uses the extra time $ TI_{attr}$ $ -$ $ TI_{min}$ to batch updates and reduce load. To implement temporal batching, PRISM defines a narrow window of time during which a node must propagate updates to its parents (assume clocks with bounded drift but not synchronized); details appear in an extended technical report [31]. However, an attribute's subtree that was unreachable over the last TI$ _{attr}$ could have been unlucky and missed its window even though it is currently reachable.

To avoid having to calculate a multitude of $ N_{reachable}$ values for different TI bounds, PRISM modifies its temporal batching protocol to ensure that each attribute's promised TI bound is met for all nodes counted as reachable. In particular, when a node receives updates from a child marked unreachable, it knows those updates may be late and may have missed their propagation window. It therefore marks such updates as NODELAY. When a node receives a NODELAY update, it processes the update immediately and propagates the result with the NODELAY flag so that temporal batching is temporarily suspended for that attribute. This modification may send extra messages in the (hopefully) uncommon case of a link performance failure and recovery, but it ensures that $ N_{reachable}$ only counts nodes that are meeting all of their TI contracts.


2 Dynamic topology

Each virtual node in PRISM caches state from its children so that when a new input from one child arrives, it can use local information to compute new values to pass up. This information is soft state--a parent discards it if a child is unreachable for a long time, similar to IGMP [28].

As a result, when a subtree chooses a new parent, that subtree's inputs may still be stored by a former parent and thus may be counted multiple times in the aggregate as shown in Figure 5(d). $ N_{dup}$ exposes this inaccuracy by bounding the number of leaves whose inputs might be included multiple times in the aggregate query result.

The basic aggregation function for $ N_{dup}$ is simple: if a subtree root spanning $ l$ leaves switches to a new parent, that subtree root inserts the value $ l$ into the $ N_{dup}$ aggregate, which has SUM as its aggregation function. Later, when sufficient time has elapsed to ensure that the node's old parent has removed its soft state, the node updates its input for the $ N_{dup}$ aggregate to 0.

Our $ N_{dup}$ implementation must deal with two issues.

  1. First, for correctness, we ensure that $ N_{dup}$ bounds the number of nodes whose inputs are double counted despite failures and network delays. We ensure this invariant by constructing a hierarchy of leases on a node's right to cache its descendent's soft state such that the leases granted by a node to its parents are always shorter than the leases the node holds from any child whose inputs are reflected in the aggregates maintained by the node.

  2. Second, for good performance, we minimize the scope of disruptions when a tree reconfigures using early expiration: a node at level $ i$ of the tree discards the state of an unresponsive subtree ($ maxLevels$ - $ i$ ) * $ t_{early}$ before its lease expires. Early expiration thereby minimizes the scope of a reconfiguration by ensuring that the parent of a failed subtree disconnects that subtree before any higher ancestor is forced to disconnect a larger subtree.

We provide further details on these aspects of the implementation in an extended technical report [31].


3 Scaling to large systems

Figure 6: The failure of a physical node has different effects on different aggregations depending on which virtual nodes are mapped to the failed physical node. The numbers next to virtual nodes show the value of $ N_{reachable}$ for each subtree after the failure of physical node 001, which acts as a leaf for one tree but as a level-2 subtree root for another.
\begin{figure}\centerline{\epsfig{figure=figures/Node001Fail.eps,width=3in}}\end{figure}

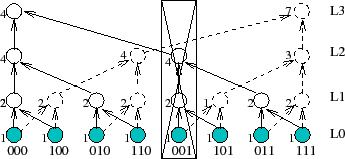
Scaling NI is a challenge. To scale attribute monitoring to a large number of nodes and attributes, PRISM constructs a forest of trees using an underlying DHT and then uses different aggregation trees for different attributes [53,39,44,5]. As Figure 6 illustrates, a failure affects different trees differently. The figure shows two aggregation trees corresponding to keys 000 and 111 for an 8-node system. In this system, the failure of the physical node with key 001 removes only a leaf node from the tree 111 but disconnects a 2-level subtree from the tree 000. Therefore, quantifying the effect of failures requires calculating the NI metrics for each of the $ n$ distinct trees in an $ n$ -node system. Making matters worse, as Section 4.1 explained, maintaining the NI metrics requires frequent active probing along each edge in each tree.

As a result of these factors, the straightforward algorithm for maintaining NI metrics separately for each tree is not tenable: the DHT forest of $ n$ degree-$ d$ aggregation trees with $ n$ physical nodes and each tree having $ \frac{n - 1/d}{1 - 1/d}$ edges ($ d>1$ ), has $ \Theta(n^2)$ edges that must be monitored; such monitoring would require $ \Theta(n)$ messages per node per probe interval. To put this overhead in perspective, consider a $ n$ =1024-node system with $ d$ =16-ary trees (i.e., a DHT with 4-bit correction per hop) and a probe interval $ p$ $ =$ $ 10s$ . The straightforward algorithm then has each node sending roughly 100 probes per second. As the system grows, the situation deteriorates rapidly--a 16K-node system requires each node to send roughly 1600 probes per second.

Our solution, described below, reduces active monitoring work to $ \Theta(\frac{d \log_d{n}}{p})$ probes per node per second. The 1024-node system in the example would require each node to send about 5 probes per second; the 16K-node system would require each node to send about 7 probes per second.

Dual tree prefix aggregation.To make it practical to maintain the NI values, we take advantage of the underlying structure of our Plaxton-tree-based DHT [44] to reuse common sub-calculations across different aggregation trees using a novel dual tree prefix aggregation abstraction.

Figure 7: Plaxton tree topology is an approximate butterfly network. Virtual node 00* in a 16-node network uses the dual tree prefix aggregation abstraction to aggregate values from a tree below it (solid bold lines) and distribute the results up a tree above it (dotted bold lines).
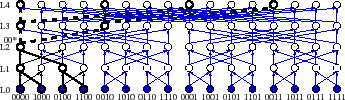\begin{figure}\centerline{\epsfig{figure=figures/butterfly-generated-by-butterfly-dot-c.eps,width=3in}}\end{figure}

As Figure 7 illustrates, this DHT construction forms an approximate butterfly network. For a degree-$ d$ tree, the virtual node at level $ i$ has an id that matches the keys that it routes in $ i\ast\log{d}$ bits. It is the root of exactly one tree, and its children are approximately $ d$ virtual nodes that match keys in $ (i-1)\ast\log{d} $ bits. It has $ d$ parents, each of which matches different subsets of keys in $ (i+1)\ast\log{d} $ bits. But notice that for each of these parents, this tree aggregates inputs from the same subtrees.

Whereas the standard aggregation abstraction computes a function across a set of subtrees and propagates it to one parent, a dual tree prefix aggregation computes an aggregation function across a set of subtrees and propagates it to all parents. As Figure 7 illustrates, each node in a dual tree prefix aggregation is the root of two trees: an aggregation tree below that computes an aggregation function across nodes in a subtree and a distribution tree above that propagates the result of this computation to a collection of enclosing aggregates that depend on this subtree for input.

For example in Figure 7, consider the level 2 virtual node 00* mapped to node 0000. This node's $ N_{reachable}$ count of 4 represents the total number of leaves included in that virtual node's subtree. This node aggregates this single $ N_{reachable}$ count from its descendants and propagates this value to both of its level-3 parents, 0000 and 0010. For simplicity, the figure shows a binary tree; by default PRISM corrects 4 bits per hop, so each subtree is common to 16 parents.


5 Case-study applications

We have developed a prototype of the PRISM monitoring system on top of FreePastry [46]. To guide the system development and to drive the performance evaluation, we have also built three case-study applications using PRISM: (1) a distributed heavy hitter detection service, (2) a distributed monitoring service for Internet-scale systems, and (3) a distribution detection service for monitoring distributed-denial-of-service (DDoS) attacks at the source-side in large-scale systems.

Figure 8: Load vs. AI and TI for (a) DHH, (b) PrMon, and (c) DDoS detection. AI and TI significantly reduce the monitoring load for the three applications; y-axis is on a log scale.
\epsfig{file=figures/abil-400.eps, width=2.4in}
\epsfig{file=figures/ci-all.eps, width=2.4in}
\epsfig{file=figures/conn-120.eps, width=2.4in}

Distributed Heavy Hitter detection (DHH). Our first application is identifying heavy hitters in a distributed system--for example, the 10 IPs that account for the most incoming traffic in the last 10 minutes [15,30]. The key challenge for this distributed query is scalability for aggregating per-flow statistics for tens of thousands to millions of concurrent flows in real-time. For example, a subset of the Abilene [1] traces used in our experiments include 260 thousand flows that send about $ 85$ million updates in an hour.

To scalably compute the global heavy hitters list, we chain two aggregations where the results from the first feed into the second. First, PRISM calculates the total incoming traffic for each destination address from all nodes in the system using SUM as the aggregation function and hash(HH-Step1, destIP) as the key. For example, tuple (H = hash(HH-Step1, 128.82.121.7), 700 KB) at the root of the aggregation tree $ T_H$ indicates that a total of 700 KB of data was received for 128.82.121.7 across all vantage points during the last time window. In the second step, we feed these aggregated total bandwidths for each destination IP into a SELECT-TOP-10 aggregation function with key hash(HH-Step2, TOP-10) to identify the TOP-10 heavy hitters among all flows.

PRISM is the first monitoring system that we are aware of to combine a scalable DHT-based hierarchy, arithmetic filtering, and temporal batching, and this combination dramatically enhances PRISM's ability to support this type of demanding application. To evaluate this application, we use multiple netflow traces obtained from the Abilene [1] backbone network where each router logged per-flow data every 5 minutes, and we replay this trace by splitting it across 400 nodes mapped to 100 Emulab [52] machines. Each node runs PRISM, and DHH application tracks the top 100 flows in terms of bytes received over a 30 second moving window shifted every 10 seconds.

Figure 8(a) shows the precision-performance results as the AI budget is varied from 0% (i.e., suppress an update if no value changes) to 20% of the maximum flow's global traffic volume and as TI is varied from 10 seconds to 5 minutes. We observe that AI of 10% reduces load by an order of magnitude compared to AI of 0 for a fixed TI of 10 seconds, by (a) culling updates for large numbers of ``mice'' flows whose total bandwidth is less than this value and (b) filtering small changes in the remaining elephant flows. Similarly, TI of 5 minutes reduces load by about 80% compared to TI of 10 seconds. For DHH application, AI filtering is more effective than TI batching for reducing load because of the large fraction of mice flows in the Abilene trace.

PrMon. The second case-study application is PrMon, a distributed monitoring service that is representative of monitoring Internet-scale systems such as PlanetLab [43] and Grid systems that provide platforms for developing, deploying, and hosting global-scale services. For instance, to manage a wide array of user services running on the PlanetLab testbed, system administrators need a global view of the system to identify problematic services (e.g., any slice consuming more than, say, 10GB of memory across all nodes on which it is running.) Similarly, users require system state information to query for lightly-loaded nodes for deploying new experiments or to track and limit the global resource consumption of their running experiments.

To provide such information in a scalable way and in real-time, PRISM computes the per-slice aggregates for each resource attribute (e.g., CPU, MEM, etc.) along different aggregation trees. This aggregate usage of each slice across all PlanetLab nodes for a given resource attribute (e.g., CPU) is then input to a per-resource SELECT-TOP-100 aggregate (e.g., SELECT-TOP-100, CPU) to compute the list of top-100 slices in terms of consumption of the resource.

We evaluate PrMon using a CoTop [11] trace from 200 PlanetLab [43] nodes at 1-second intervals for 1 hour. The CoTop data provide the per-slice resource usage (e.g., CPU, MEM, etc.) for all slices running on a node. Using these logs as sensor input, we run PrMon on 200 servers mapped to 50 Emulab machines. Figure 8(b) shows the combined effect of AI and TI in reducing PrMon's load for monitoring global resource usage per slice. We observe AI of 1% reduces load by 30x compared to AI of 0 for fixed TI of 10 seconds. Likewise, compared to TI of 10 seconds and AI of 0, TI of 5 minutes reduces overhead per node by 20x. A key benefit of PRISM's tunable precision is the ability to support new, highly-responsive monitoring applications: for approximately the same bandwidth cost as retrieving node state every 5 minutes (TI = 5 minutes, no AI filtering), PRISM provides highly time-responsive and accurate monitoring with TI of 10 seconds and AI of 1%.

DDoS detection at the source. The final monitoring application is DDoS detection to keep track of which nodes are receiving a large number of traffic (bytes, packets) from PlanetLab. This application is important to prevent PlanetLab from being used maliciously or inadvertently to launch DDoS traffic (which has, indeed, occurred in the past [2]). For input, we collect a trace of traffic statistics--number of packets sent, number of bytes sent, network protocol, source and destination IP addresses, and source and destination ports--every 15 seconds for four hours using Netfilter's connection tracking interface /proc/net/ip_conntrack for all slices from 120 PlanetLab nodes. Each node's traffic statistics are fed into PRISM to compute the aggregate traffic sent to each destination IP across all nodes. Each destination's aggregate value is fed, in turn, to a SELECT-TOP-100 aggregation function to compute a top-100 list of destination IP addresses that receive the highest aggregate traffic (bytes, packets) at two time granularities: (1) a 1 minute sliding window shifted every 15 seconds and (2) a 15 minute sliding window shifted every minute.

Figure 8(c) shows running the application on 120 PRISM nodes mapped to 30 department machines. The AI budget is varied from 0% to 20% of the maximum flow's global traffic volume (bytes, packets) at both the 1 minute and 15 minutes time windows, and TI is varied from 15 seconds to 5 minutes. We observe that AI of 1% reduces load by 30x compared to AI of 0% by filtering most flows that send little traffic. Overall, AI and TI reduce load by up to 100x and 8x, respectively, for this application.

Figure 9: NI metrics under system churn: (a) single node failure at 70 seconds for 108 Emulab nodes, (b) periodic failures for 108 Emulab nodes, and (c) 85 PlanetLab nodes with no synthetic failures.
\epsfig{file=figures/NI-micro-10mins.eps,width=2.4in}
$ ~~~~~~~~~~~~~~~~~$ (a)
\epsfig{file=figures/NI-micro-periodic-4h.eps, width=2.4in}
$ ~~~~~~~~~~~~~~~~~$ (b)
\epsfig{file=figures/plstate.eps, width=2.4in}
$ ~~~~~~~~~~~~~~~~~$ (c)


6 Experimental Evaluation

As illustrated above, our initial experience with PRISM is encouraging: PRISM's load-balanced DHT-based hierarchical aggregation, arithmetic filtering, and temporal batching provide excellent scalability and enable demanding new monitoring applications. However, as discussed in Section 2, this scalability comes at a price: the risk that query results depart significantly from reality in the presence of failures.

This section therefore focuses on a simple question: can NI safeguard accuracy in monitoring systems that use hierarchy, arithmetic filtering, or temporal batching for scalability? We first investigate PRISM's ability to use NI to qualify the consistency guarantees promised by AI and TI, then explore the consistency/availability trade-offs that NI exposes, and finally quantify the overhead in computing the NI metrics. Overall, our evaluation shows that NI enables PRISM to be an effective substrate for accurate scalable monitoring: the NI metrics characterize system state and reduce measurement inaccuracy while incurring low communication overheads.


1 Exposing disruption

In this section, we illustrate how PRISM uses NI to expose overlay disruptions that could significantly affect monitoring applications.

We first illustrate how NI metrics reflect network state in two controlled experiments in which we run 108 PRISM nodes on Emulab. In Figure 9(a) we kill a single node 70 seconds into the run, which disconnects 24 additional nodes from the aggregation tree being examined. Within seconds, this failure causes $ N_{reachable}$ to fall to 83, indicating that any result calculated in this interval might only include the most recent values from 83 nodes. Pastry detects this failure quickly in this case and reconfigures, causing the disconnected nodes to rejoin the tree at a new location. These nodes contribute 24 to $ N_{dup}$ until they are certain that their former parent is no longer caching their inputs as soft state. The glitch for $ N_{all}$ occurs because the disconnected children rejoin the system slightly more quickly than their prior ancestor detects their departure. Figure 9(b) traces the evolution of the NI metrics as we kill one of the 108 original nodes every 10 minutes over a 4 hour run, and similar behaviors are evident; we use higher churn than typical environments to stress test the system. Figure 9(c) shows how NI reflects network state for a 85-node PrMon experiment on PlanetLab for an 18-hour run; nodes were randomly picked from 248 Internet2 nodes. For some of the following experiments we focus on NI's effectiveness during periods of instability by running experiments on PlanetLab nodes. Because these nodes show heavy load, unexpected delays, and relatively frequent reboots (especially prior to deadlines!), we expect these nodes to exhibit more NI than a typical environment, which makes them a convenient stress test of our system.

Figure 10: Validation of NI metrics: NI has (a) few false positives and (b) almost zero false negatives.
\epsfig{file=figures/Emu-FP.eps, width=1.75in}
$ ~~~~~~~~~~~~~~~~~~~~~~$ (a)
\epsfig{file=figures/Emu-FN.eps, width=1.75in}
$ ~~~~~~~~~~~~~~~~~~~$ (b)
Figure 11: (a) and (b) show the CDFs of result accuracy with answers filtered for different NI thresholds and $ k$ = 1 for PrMon on (a) Planetlab and (b) Emulab. (c) Shows the availability of results on Planetlab by showing the CDF of NI values for $ k$ duplicate keys.
\epsfig{file=figures/ni-dev.eps, width=2.4in}
$ ~~~~~~~~~~~~~~~~$ (a) CDF of result accuracy (PlanetLab)
\epsfig{file=figures/ni-dev-emulab-k1.eps, width=2.4in}
$ ~~~~~~~~~~~~~~~~~~~$ (b) CDF of result accuracy (Emulab)
\epsfig{file=figures/ni-cdf.eps, width=2.4in}
$ ~~~~~~~~~~~~~~~~~$ (c) CDF of observed NI (PlanetLab)
Our implementation of NI is conservative: we are willing to accept some false positives (when NI reports that inputs are stale or duplicated when they are not, as discussed in Section 4.1), but we want to minimize false negatives (when NI fails to warn an application of duplicate or stale inputs). Figure 10 shows the results for a 96-node Emulab setup under a network path failure model [13]; we use failure probability, MTTF, and MTTR of 0.1, 3.2 hours, and 10 minutes. We contrive an ``append'' aggregation in each of the 96 distinct trees: each node periodically feeds a (node, timestamp) tuple and internal nodes append the children inputs together. At each root, we compare the aggregate value against NI to detect any false positive (FP) or false negative (FN) reports for (1) $ N_{dup}$ count duplicates and (2) dips in $ N_{reachable}$ count nodes whose reported values are not within TI of their current values.

Figure 10 indicates that NI accurately characterizes how churn affects aggregation. Across 300 minutes and 96 trees, we observe fewer than 100 false positive reports, most of them small in magnitude. The high FP near 60 minutes is due to a root failure triggering a large reconfiguration and was validated using logs. We observe zero false negative reports for unreachability and three false negative reports for duplication; the largest error was underreporting the number of duplicate nodes by three. Overall, we observe a FP rate less than 0.3% and a FN rate less than 0.01%.

2 Coping with disruption

We now examine how applications use NI to improve their accuracy by compensating for churn. Our basic approach is to compare results of NI-oblivious aggregation and aggregation with NI-based compensation with an oracle that has access to the inputs at all leaves; we simulate the oracle via off-line processing of input logs. We run a 1 hour trace-based PrMon experiment on 94 PlanetLab nodes or 108 Emulab nodes for a collection of attributes calculated using a SUM aggregate with AI = 0 and TI = 60 seconds. For Emulab, we use the synthetic failure model described for Fig 10. Note that to keep the discussion simple, we condense NI to a single parameter: NI = $ \big(\frac{N_{all} - N_{reachable}}{N_{all}}\big)$ + $ \big(\frac{N_{dup}}{N_{all}}\big)$ for all the subsequent experiments.

The NI-oblivious line of Figure 11(a) and (b) shows for PrMon nodes that ignore NI, the CDF of the difference between query results and the true value of the aggregation computed by an off-line oracle from traces. For PlanetLab, 50% of the reports differ from the truth by more than 30% in this challenging environment. For the more stable Emulab environment, a few results differ from reality by more than 40%. Next, we discuss how applications can achieve better accuracy using techniques discussed in Section 3.3.

Filtering. One technique is to trade availability for accuracy by filtering results during periods of instability. The lines (NI $ < x$ %, $ x =$ 5, 10, 50, 75, and 90) of Figure 11(a) and (b) show how rejecting results with high NI improves accuracy. For example, for the high-churn PlanetLab environment, when NI $ <$ 5%, 80% answers have less than 20% deviation from the true value. For the Emulab experiment, 95% answers have less than 20% deviation using NI $ <$ 5% filtering.

Filtering answers during periods of high churn exposes a fundamental consistency versus availability tradeoff [19]. Applications must decide whether it is better to silently give a potentially inaccurate answer or explicitly indicate when it cannot provide a good answer. For example, the $ k=1$ line in Figure 11(c) shows the CDF of the fraction of time for which NI is at or below a specified value for the PlanetLab run. For half of the reports, NI $ >$ 30% and for 20% of the reports, NI $ >$ 80% reflecting high system instability. Note that the PlanetLab environment is intended to illustrate PRISM's behavior during intervals of high churn. Since accuracy is maximized when answers reflect complete and current information, systems with fewer disruptions (e.g., Emulab) are expected to show higher result accuracy compared to PlanetLab and we observe this behavior for Emulab where the curves in Figure 11(c) shift up and to the left (graph omitted due to space constraints; please see the technical report [31]).

Figure 12: CDF of result accuracy for redundant aggregation up $ k$ trees and filtering for PlanetLab and Emulab runs for the PrMon application.
\epsfig{file=figures/ni-ub-varyk.eps, width=2.4in}
$ ~~~~~~~~~~~~~~~~~~$ (a) PlanetLab redun. aggr.
\epsfig{file=figures/ni-dev-plab-filterdup.eps, width=2.4in}
$ ~~~~~~~~~~~~~~~$ (b) PlanetLab redun. aggr. + filtering
\epsfig{file=figures/ni-dev-emulab-filterdup.eps, width=2.4in}
$ ~~~~~~~~~~~~~~~~$ (c) Emulab redun. aggr. + filtering

Redundant aggregation. Redundant aggregation allows applications to trade increased overheads for better availability and accuracy. Rather than aggregating an attribute up a single tree, information can be aggregated up $ k$ distinct trees. As $ k$ increases, the fraction of time during which NI is low increases. Because the vast majority of nodes in a 16-ary tree are near the leaves, sampling several trees rapidly increases the probability that at least one tree avoids encountering many near-root failures. We provide an analytic model formalizing this intuition in a technical report [31].

In Figure 12(a) we explore the effectiveness of a simple redundant aggregation approach in which PrMon aggregates each attribute $ k$ times and then chooses the result with the lowest NI. This approach maximizes availability--as long as any of the root nodes for an attribute are available, PrMon always returns a result--and it also can achieve high accuracy. Due to space constraints, we focus on the PlanetLab run and show the CDF of results with respect to the deviation from an oracle as we vary $ k$ from 1 to 4. We observe that this approach can reduce the deviation to at most 22% thereby reducing the worst-case inaccuracy by nearly 5x.

Applications can combine the redundant aggregation and filtering techniques to get excellent availability and accuracy. Figure 12(b) and (c) show the results for the PlanetLab and Emulab environments. As Figure 11(c) shows, redundant aggregation increases availability by increasing the fraction of time NI is below the filter threshold, and as Figures 12(b) and (c) show, the combination improves accuracy by up to an order of magnitude over best effort results.

3 NI scalability

Finally, we quantify the monitoring overhead of tracking NI via (1) each aggregation tree separately and (2) dual-tree prefix aggregation. Figure 13 shows the average per-node message cost for NI monitoring as we vary the network size from 16 to 1024 nodes mapped to 256 Lonestar [35] machines. We observe that the overhead using independent aggregation trees scales linearly with the network size whereas it scales logarithmically using dual-tree prefix aggregation.

Note that the above experiment constructs all $ n$ distinct trees in the DHT forest of $ n$ nodes assuming that the number of attributes is at least on the order of the number of nodes $ n$ . However, for systems that aggregate fewer attributes (or if only few attributes care about NI), it is important to know which of the two techniques for tracking NI--(1) per-tree aggregation or (2) dual-tree prefix aggregation--is more efficient. Figure 14 shows both the average and the maximum message cost across all nodes in a 1000-node experimental setup as above for both per-tree NI aggregation and dual-tree prefix aggregation as we increase the number of trees along which NI value is computed. Note that per-tree NI aggregation costs increase as we increase the number of trees while dual-tree prefix aggregation has a constant cost. We observe that the break-even point for the average load is 44 trees while the break-even point for the maximum load is only 8 trees.

Figure 13: NI monitoring overhead for dual-tree prefix aggregation and for computing NI per aggregation tree. The overhead scales linearly with the network size for per-tree aggregation whereas it scales logarithmically using dual-tree prefix aggregation.
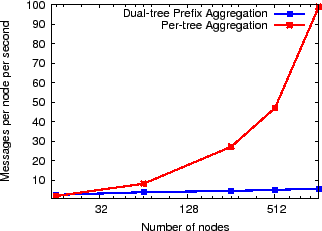
\epsfig{file=figures/ni-scale.eps, width=3.0in}
Figure: Break-even point for NI tracking overhead as the number of trees (attributes) varies for (a) per-tree aggregation vs. (b) dual-tree prefix aggregation in a 1000-node system. The break-even points for the average and maximum load are 44 trees and 8 trees.
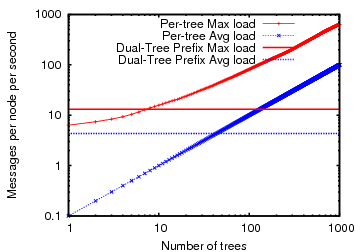
\epsfig{file=figures/pertree-vs-dual-1024/pertree-dual-breakeven.ps,width=3.0in}


7 Related Work

PRISM is a monitoring architecture that is to our knowledge the first to maximize scalability by integrating three techniques that have been used in isolation in prior systems: DHT-based hierarchy for load balancing and in-network filtering [5,44,47,53], arithmetic filtering [6,21,38,30,31,36,42,51,56], and temporal batching [56,36,14]. As discussed in Section 2, each of these techniques improves scalability, but each also increases the risk that queries will report incorrect results during network and node failures. We believe the NI abstraction and the implementation techniques discussed in this paper will be widely applicable.

The idea of flagging results when the state of a distributed system is disrupted by node or network failures has been used in tackling other distributed systems problems. For example, our idea of NI is analogous to that of fail-aware services [16] and failure detectors [9] for fault-tolerant distributed systems. Freedman et al. propose link-attestation groups [18] that use an application specific notion of reliability and correctness to map pairs of nodes which consider each other reliable. Their system, designed for groups on the scale of tens of nodes, monitors the nodes and system and exposes such attestation graph to the applications. Bawa et al. [4] survey previous work on measuring the validity of query results in faulty networks. Their ``single-site validity'' semantic is equivalent to PRISM's $ N_{reachable}$ metric. Completeness [20] defined as the percentage of network hosts whose data contributed to the final query result, is similar to the ratio of $ N_{reachable}$ and $ N_{all}$ . Relative Error [12,57] between the reported and the ``true'' result at any instant can only be computed by an oracle with a perfect view of the dynamic network.

Several aggregation systems have worked to address the failure amplification effect. To mask failures, TAG [36] proposes (1) reusing previously cached values and (2) dividing the aggregate value into fractions equal to the number of parents and then sending each fraction to a distinct parent. This approach reduces the variance but not the expected error of the aggregate value at the root. SAAR uses multiple interior-node-disjoint trees to reduce the impact of node failures [39]. In San Fermin [8], each node creates its own binomial tree by swapping data with other nodes. Seaweed [40] uses a supernode approach in which data on each internal node is replicated. However, both these systems process one-shot queries but not continuous queries on high-volume dynamic data, which is the focus of PRISM. Gossip-based protocols [51,45,7] are highly robust but incur more overhead than trees [53]. NI can also complement gossip protocols, which we leave as future work. Other studies have proposed multi-path routing methods [29,20,12,41,37] for fault-tolerant aggregation.

Recent proposals [37,12,41,4,55] have combined multipath routing with order- and duplicate-insensitive data structures to tolerate faults in sensor network aggregation. The key idea is to use probabilistic counting [17] to approximately count the number of distinct elements in a multi-set. PRISM takes a complementary approach: whereas multipath duplicate-insensitive (MDI) aggregation seeks to reduce the effects of network disruption, PRISM's NI metric seeks to quantify the network disruptions that do occur. In particular, although MDI aggregation can, in principle, reduce network-induced inaccuracy to any desired target if losses are independent and sufficient redundant transmissions are made [41], the systems studied in the literature are still subject to non-zero network-induced inaccuracy due to efforts to balance transmission overhead with loss rates, insufficient redundancy in a topology to meet desired path redundancy, or correlated network losses across multiple links. These issues may be more severe in our environment than in wireless sensor networks targeted by MDI approaches because the dominant loss model may differ (e.g., link congestion and DHT reconfigurations in our environment versus distance-sensitive loss probability for the wireless sensors) and because the transmission cost model differs (for some wireless networks, transmission to multiple destinations can be accomplished with a single broadcast.

The MDI aggregation techniques are also complementary in that PRISM's infrastructure provides NI information that is common across attributes while the MDI approach modifies the computation of individual attributes. As Section 3.3 discussed, NI provides a basis for integrating a broad range of techniques for coping with network error, and MDI aggregation may be a useful technique in cases when (a) an aggregation function can be recast to be order- and duplicate-insensitive and (b) the system is willing to pay the extra network cost to transmit each attribute's updates. To realize this promise, additional work is required to extend MDI approaches for bounding the approximation error while still minimizing network load via AI and TI filtering.


8 Conclusions

If a man will begin with certainties, he shall end in doubts; but if he will be content to begin with doubts, he shall end in certainties.
-Sir Francis Bacon

We have presented Network Imprecision, a new metric for characterizing network state that quantifies the consistency of query results in a dynamic, large-scale monitoring system. Without NI guarantees, large scale network monitoring systems may provide misleading reports because query result outputs by such systems may be arbitrarily wrong. Incorporating NI in the PRISM monitoring framework qualitatively improves its output by exposing cases when approximation bounds on query results can not be trusted.

<<2630>>

9 Acknowledgments

We thank our shepherd Dejan Kostic, Joe Hellerstein, and the anonymous reviewers for their valuable feedback. Navendu Jain is supported by an IBM Ph.D. Fellowship. This work is supported in part by NSF Awards CNS-0546720, CNS-0627020 and SCI-0438314.

Bibliography

1
Abilene Internet2 Network.
https://abilene.internet2.edu/.

2
R. Adams.
Distributed system management: PlanetLab incidents and management tools.
Technical Report PDN-03-015, PlanetLab Consortium, 2003.

3
B. Babcock, S. Babu, M. Datar, R. Motwani, and J. Widom.
Models and issues in data stream systems.
In PODS, 2002.

4
M. Bawa, A. Gionis, H. Garcia-Molina, and R. Motwani.
The price of validity in dynamic networks.
In SIGMOD, 2004.

5
A. Bharambe, M. Agrawal, and S. Seshan.
Mercury: Supporting Scalable Multi-Attribute Range Queries.
In SIGCOMM, 2004.

6
M. Bhide, K. Ramamritham, and M. Agrawal.
Efficient execution of continuous incoherency bounded queries over multi-source streaming data.
In ICDCS, 2007.

7
Y. Birk, I. Keidar, L. Liss, and A. Schuster.
Efficient dynamic aggregation.
In DISC, 2006.

8
J. Cappos and J. H. Hartman.
San fermín: aggregating large data sets using a binomial swap forest.
In NSDI, 2008.

9
T. Chandra and S. Toueg.
Unreliable failure detectors for reliable distributed systems.
J. ACM, 1996.

10
D. D. Clark, C. Partridge, J. C. Ramming, and J. Wroclawski.
A knowledge plane for the Internet.
In SIGCOMM, 2003.

11
Comon.
https://comon.cs.princeton.edu/.

12
J. Considine, F. Li, G. Kollios, and J. Byers.
Approximate aggregation techniques for sensor databases.
In ICDE, 2004.

13
M. Dahlin, B. Chandra, L. Gao, and A. Nayate.
End-to-end WAN service availability.
IEEE/ACM Transactions on Networking, 2003.

14
A. Deshpande, S. Nath, P. Gibbons, and S. Seshan.
Cache-and-query for wide area sensor databases.
In SIGMOD, 2003.

15
C. Estan and G. Varghese.
New directions in traffic measurement and accounting.
In SIGCOMM, 2002.

16
C. Fetzer and F. Cristian.
Fail-awareness in timed asynchronous systems.
In PODC, 1996.

17
P. Flajolet and G. N. Martin.
Probabilistic counting algorithms for data base applications.
JCSS, 1985.

18
M. J. Freedman, I. Stoica, D. Mazieres, and S. Shenker.
Group therapy for systems: Using link attestations to manage failures.
In IPTPS, 2006.

19
S. Gilbert and N. Lynch.
Brewer's conjecture and the feasibility of Consistent, Available, Partition-tolerant web services.
In ACM SIGACT News, 33(2), Jun 2002.

20
I. Gupta, R. van Renesse, and K. P. Birman.
Scalable fault-tolerant aggregation in large process groups.
In DSN, 2001.

21
R. Gupta and K. Ramamritham.
Optimized query planning of continuous aggregation queries in dynamic data dissemination networks.
In WWW, pages 321-330, 2007.

22
N. J. A. Harvey, M. B. Jones, S. Saroiu, M. Theimer, and A. Wolman.
SkipNet: A Scalable Overlay Network with Practical Locality Properties.
In USITS, March 2003.

23
J. M. Hellerstein, V. Paxson, L. L. Peterson, T. Roscoe, S. Shenker, and D. Wetherall.
The network oracle.
IEEE Data Eng. Bull., 2005.

24
M. Herlihy and J. Wing.
Linearizability: A correctness condition for concurrent objects.
ACM Trans. Prog. Lang. Sys., 12(3), 1990.

25
E. Hoke, J. Sun, J. D. Strunk, G. R. Ganger, and C. Faloutsos.
Intemon: continuous mining of sensor data in large-scale self-infrastructures.
Operating Systems Review, 40(3):38-44, 2006.

26
L. Huang, M. Garofalakis, A. D. Joseph, and N. Taft.
Communication-efficient tracking of distributed cumulative triggers.
In ICDCS, 2007.

27
R. Huebsch, J. M. Hellerstein, N. Lanham, B. T. Loo, S. Shenker, and I. Stoica.
Querying the Internet with PIER.
In VLDB, 2003.

28
Internet group management protocol, version 2.
https://www.ietf.org/rfc/rfc2236.txt.

29
C. Intanagonwiwat, R. Govindan, and D. Estrin.
Directed diffusion: a scalable and robust communication paradigm for sensor networks.
In MobiCom, 2000.

30
N. Jain, D. Kit, P. Mahajan, P. Yalagandula, M. Dahlin, and Y. Zhang.
STAR: Self tuning aggregation for scalable monitoring.
In VLDB, 2007.

31
N. Jain, P. Mahajan, D. Kit, P. Yalagandula, M. Dahlin, and Y. Zhang.
Network Imprecision: A new consistency metric for scalable monitoring (extended).
Technical Report TR-08-40, UT Austin Department of Computer Sciences, October 2008.

32
N. Jain, P. Yalagandula, M. Dahlin, and Y. Zhang.
Self-tuning, bandwidth-aware monitoring for dynamic data streams.
In ICDE, 2009.

33
L. Lamport.
Time, clocks, and the ordering of events in a distributed system.
Comm. of the ACM, 21(7), July 1978.

34
L. Lamport.
How to make a multiprocessor computer that correctly executes multiprocess programs.
IEEE Transactions on Computers, C-28(9):690-691, Sept. 1979.

35
Ranger HPC Cluster.
https://www.tacc.utexas.edu/resources/hpcsystems.

36
S. R. Madden, M. J. Franklin, J. M. Hellerstein, and W. Hong.
TAG: a Tiny AGgregation Service for Ad-Hoc Sensor Networks.
In OSDI, 2002.

37
A. Manjhi, S. Nath, and P. B. Gibbons.
Tributaries and deltas: efficient and robust aggregation in sensor network streams.
In SIGMOD, 2005.

38
A. Manjhi, V. Shkapenyuk, K. Dhamdhere, and C. Olston.
Finding (recently) frequent items in distributed data streams.
In ICDE, 2005.

39
A. Nandi, A. Ganjam, P. Druschel, T. S. E. Ng, I. Stoica, H. Zhang, and B. Bhattacharjee.
SAAR: A shared control plane for overlay multicast.
In NSDI, 2007.

40
D. Narayanan, A. Donnelly, R. Mortier, and A. I. T. Rowstron.
Delay aware querying with seaweed.
In VLDB, 2006.

41
S. Nath, P. B. Gibbons, S. Seshan, and Z. R. Anderson.
Synopsis diffusion for robust aggregation in sensor networks.
In SenSys, 2004.

42
C. Olston, J. Jiang, and J. Widom.
Adaptive filters for continuous queries over distributed data streams.
In SIGMOD, 2003.

43
Planetlab.
https://www.planet-lab.org.

44
C. G. Plaxton, R. Rajaraman, and A. W. Richa.
Accessing Nearby Copies of Replicated Objects in a Distributed Environment.
In ACM SPAA, 1997.

45
B. Raghavan, K. V. Vishwanath, S. Ramabhadran, K. Yocum, and A. C. Snoeren.
Cloud control with distributed rate limiting.
In SIGCOMM, 2007.

46
A. Rowstron and P. Druschel.
Pastry: Scalable, Distributed Object Location and Routing for Large-scale Peer-to-peer Systems.
In Middleware, 2001.

47
J. Shneidman, P. Pietzuch, J. Ledlie, M. Roussopoulos, M. Seltzer, and M. Welsh.
Hourglass: An Infrastructure for Connecting Sensor Networks and Applications.
Technical Report TR-21-04, Harvard University, 2004.

48
A. Silberstein, G. Puggioni, A. Gelfand, K. Munagala, and J. Yang.
Suppression and failures in sensor networks: A Bayesian approach.
In VLDB, 2007.

49
I. Stoica, R. Morris, D. Karger, F. Kaashoek, and H. Balakrishnan.
Chord: A scalable peer-to-peer lookup service for Internet applications.
In ACM SIGCOMM, 2001.

50
E. Thereska, B. Salmon, J. D. Strunk, M. Wachs, M. Abd-El-Malek, J. Lopez, and G. R. Ganger.
Stardust: tracking activity in a distributed storage system.
In SIGMETRICS/Performance, pages 3-14, 2006.

51
R. van Renesse, K. Birman, and W. Vogels.
Astrolabe: A robust and scalable technology for distributed system monitoring, management, and data mining.
TOCS, 21(2):164-206, 2003.

52
B. White, J. Lepreau, L. Stoller, R. Ricci, S. Guruprasad, M. Newbold, M. Hibler, C. Barb, and A. Joglekar.
An integrated experimental environment for distributed systems and networks.
In OSDI, 2002.

53
P. Yalagandula and M. Dahlin.
A scalable distributed information management system.
In SIGCOMM, Aug. 2004.

54
P. Yalagandula, P. Sharma, S. Banerjee, S.-J. Lee, and S. Basu.
S$ ^{3}$ : A Scalable Sensing Service for Monitoring Large Networked Systems.
In SIGCOMM Wkshp. on Internet Network Mgmt, 2006.

55
H. Yu.
Dos-resilient secure aggregation queries in sensor networks.
In PODC, pages 394-395, 2007.

56
H. Yu and A. Vahdat.
Design and evaluation of a conit-based continuous consistency model for replicated services.
TOCS, 2002.

57
Y. Zhao, R. Govindan, and D. Estrin.
Computing aggregates for monitoring wireless sensor networks.
In SNPA, 2003.

About this document ...

Network Imprecision: A New Consistency Metric for Scalable Monitoring

This document was generated using the LaTeX2HTML translator Version 2008 (1.71)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation head.tex

The translation was initiated by Navendu Jain on 2008-10-20

Navendu Jain
2008-10-20