
OSDI '06 Paper
Pp. 191–204 of the Proceedings
BAR Gossip
Harry C. Li, Allen Clement, Edmund L. Wong, Jeff
Napper, Indrajit Roy,
Lorenzo Alvisi, Michael Dahlin
Laboratory for Advanced Systems Research (LASR),
Dept. of Computer Sciences,
The University of Texas at Austin
1 Introduction
Streaming media is an increasingly useful application at several
scales of deployment. For example, the 2006 NCAA tournament had peak
participation of 150k+ users for their live streaming services. At
smaller scales, such as academic conferences like OSDI or artistic
events like Austin's SXSW that draw audiences of dozens to hundreds
of people, there is interest in providing a live stream, but little
existing infrastructure to support it.
At all these scales, a peer-to-peer (p2p) streaming solution appears
to be an intriguing alternative to traditional methods. One advantage
of p2p systems is their potential to be highly robust, scalable, and
adaptive. For example, a p2p architecture could, in principle, absorb
the impact of an unexpected flash crowd. Furthermore, large-scale
content providers may adopt p2p-based solutions to shift costs (like
bandwidth) to clients, and small-scale providers might find it simpler
to use a self-organizing p2p network instead of provisioning and
maintaining a large dedicated server.
Realizing the promises of p2p in streaming services is
non-trivial. First, the service must guarantee highly reliable,
stable, and timely throughput of messages despite the presence of
faulty, misconfigured, or even malicious peers. Second, the service
must be robust against selfish users, who try to catch a free
ride by receiving streams without contributing their fair share to
other users [12]. The free-rider phenomenon in p2p
systems is a symptom of a broader issue: any system deployed across
multiple administrative domains must be designed for the possibility
that nodes will deviate from their specification if doing so is
advantageous. File-sharing p2p applications, like
BitTorrent [7], have recognized this issue and
introduced a set of heuristics to incentivize faithful
participation--these heuristics, however, optimize for bulk file
transfer, not for the timely delivery of a series of small frames
required by a streaming service.
This paper presents the first p2p streaming media application designed
for a system model (BAR [1]) in which altruistic
nodes (who follow the protocol assigned to them) coexist with both
arbitrarily malicious (Byzantine) and self-serving ( rational) nodes. Our BAR-tolerant solution, based on gossip
protocols [4,8,19,35],
provides a scalable mechanism for information dissemination that
ensures predictable throughput even if all of the nodes act selfishly
and the remainder act maliciously or malfunction in arbitrary ways.
The defining characteristic of gossip protocols is that each node
exchanges data, or gossips, with randomly selected
peers: it is precisely this randomness that gives gossip protocols
their enviable robustness. From the perspective of designing
BAR-tolerant protocols, however, randomness can be a real headache: in
fact, any source of non-determinism is hard to deal with in the
BAR model because it gives opportunities for rational users to hide
selfish actions in the guise of legitimate, non-deterministic
behavior.
We overcome this difficulty by building a BAR-tolerant gossip protocol
that uses verifiable pseudo-randomness as the means for peer
selection: in particular, we exploit properties of pseudo-random
number generators and unique signature schemes to build a verifiable
pseudo-random partner selection algorithm. This approach eliminates
the main source of non-determinism in traditional gossip--randomness
in partner selection--yet maintains the unpredictability and rapid
convergence of traditional gossip. Our novel peer selection
technique, in combination with a simple fair enough exchange
mechanism based on the notion of credible
threats [1,9], proves effective in
encouraging the fair exchange [17] of one node's
updates for another's. We believe that enticing cooperation over
short timescales is simpler and more robust than approaches based on
long-term
reputations [16,36,23]
because doing so limits Brutus attacks, in which malicious nodes
maximize damage by earning the trust of their victims before striking.
We build a prototype streaming application that uses our BAR Gossip
protocol to provide a stable throughput multicast. We show that BAR
Gossip is robust to Byzantine and selfish behavior, even when 40% of
selfish nodes collude. In an environment in which 20% of clients are
Byzantine and the remaining are rational, we demonstrate that if the
broadcaster can multicast packets to a constant number of random
nodes, then non-Byzantine clients can reliably deliver the stream in a
timely manner.
In this paper, we make two main technical contributions:
- We design BAR Gossip, the first gossip protocol resilient to
both Byzantine and selfish behavior.
- We use BAR gossip to build the first p2p streaming application
to guarantee predictable throughput and low latency in the BAR model.
More broadly, by showing that it is possible to derive BAR tolerant
versions of a highly non-deterministic protocol such as gossip, we
believe this work strengthens the case for BAR tolerance as the right
model for reasoning about the dependability of systems deployed across
multiple administrative domains.
We introduce the paper in Section 1, which ends with this
paragraph outlining the rest of the paper. Section 2
frames our contributions in the context of previous work. The system
model is described in Section 3. Section 4
then describes BAR Gossip, followed by Section 5,
which supports our claim that BAR Gossip is a robust streaming
protocol through a combination of simulations and live experiments.
BAR Gossip targets streaming of live content among Byzantine,
altruistic, and rational nodes. It draws on a broad literature of bulk
file transfer systems designed to tolerate node misbehavior as well as
a large number of efforts to use gossip for robust data dissemination.
Several systems have addressed selfish behavior in p2p content
distribution. BitTorrent [7] leverages a local
reputation scheme for file-sharing in which nodes give preference to
those peers who have reliably reciprocated in the past.
Scrivener [27] generalizes BitTorrent by supporting
a distributed reputation scheme based on credits that can be earned
and redeemed across multiple files: through this mechanism, a
Scrivener node that has been a good citizen can enlist the help of its
peers even if the file it wants to acquire is unpopular.
Habib and Chuang [15] study p2p streaming of
non-live media in a selfish environment. They use distributed
reputations in the form of global rankings to deter free-riders while
providing good quality streams to cooperative clients.
FOX [18] guarantees optimal download time to all the
nodes interested in acquiring the same file under the assumption that
all nodes are selfish. This guarantee, however, comes at the expense
of robustness: the system's incentive structure depends on the fear of
mutual assured destruction, and a single Byzantine node can cause the
entire system to collapse.
Splitstream [6] is a tree-based multicast
protocol that achieves load balancing by dividing content into
multiple stripes, each of which is multicast using a separate
tree. Splitstream is vulnerable to freeloaders. Ngan et
al. [30] observe that if Splitstream's multicast
trees are periodically rebuilt and nodes maintain local reputations
regarding nodes that have misbehaved, then upstream nodes in a given
tree have an incentive to provide good service to downstream nodes to
avoid future retaliation.
BAR Gossip differs from these systems in four key ways. First, these
systems work to optimize average download bandwidth over long periods
of time and do not attempt to maintain stable throughput over shorter
intervals. In contrast, our protocol is designed to disseminate live
streams and therefore values the highly reliable, stable, and timely
throughput that comes with gossip-style data dissemination. Second,
several of these systems are designed to be robust to
Byzantine [6] or
rational [15,18,27] players
but not both. Third, all of these systems transfer a large collection
of file blocks. In contrast, BAR Gossip distributes live streams and
must cope with having a relatively small window of ``useful'' data in
flight at any given time; ensuring timely delivery of a small set of
data is one of the key challenges in our protocol. Fourth, most of
these systems make use of
local [7,30] or
distributed [27,15] node reputations
in their incentive structure. But given our desire to provide stable
throughput over short periods of time, relying on a node's long-term
reputation to predict its short-term behavior is problematic.
Furthermore, because gossip partners are likely to change in every
round, in our protocol it is virtually impossible for a node to build
enough good will with specific partners to support a purely local
reputation scheme à la BitTorrent. Additionally, it appears
challenging to implement a strategy-proof reputation system in an
environment with both rational and Byzantine players.
Gossip algorithms were first introduced by Demers et
al. [8] to manage replica consistency in the Xerox
Clearinghouse Service [31]. Following Birman
et al.'s highly influential paper on Bimodal
Multicast [4], gossip algorithms have established
themselves as one of the leading approaches to achieve reliable and
scalable application-level
multicast [5,11,14,19,25,40].
Gossip protocols are also at the core of a new generation of scalable
distributed protocols for failure detection [35],
group communication [13,39], and the
monitoring and management of large distributed
systems [38].
Experience with the CoolStream implementation of the DONet p2p overlay
network [41] makes a strong case for the scalability of
gossip-based dissemination of live streams and for its potential
to deliver high quality end-to-end user experience in the presence of
altruistic nodes.
Secure gossiping aims to prevent Byzantine nodes from spreading false
updates. While digital signatures are not necessary to accomplish this
goal [20,21,22,26],
they considerably simplify protocol design and are assumed in most
practical gossip-based
systems [5,38,39],
including BAR Gossip.
DRUM [2] assumes secure gossip and focuses
on fighting denial of service (DoS) attacks through two main
techniques: bounding the resources allocated to each gossip
operation and directing these operations to random ports.
Aiyer et al. [1] define a replicated state machine
protocol under the BAR model. Although the replication overheads of
that approach are too high for live streaming media, we draw on many
of the same design principles: predictable communication
patterns manifest in our partner selection algorithm
(Section 4.2.1), cost balancing manifests in
our optimistic push algorithm (4.2.5), credible
threats manifest in our key exchange (4.2.4), and ensuring long term benefit manifests in our delayed gratification
protocol structure (4.1).
We consider the problem of streaming a live event across the Internet
where the audience members, which we call clients, help
disseminate stream packets.
Clients can be Byzantine, altruistic, or rational. Each rational
client follows a strategy that maximizes its utility. Rational clients
share a utility function that describes costs and benefits; in this
paper, the benefit consists in the ability to play the live stream and
the costs are incurred by sending and receiving packets. A rational
client deviates from the specification if and only if doing so
increases that client's expected utility. We assume that a rational
client's benefit from timely acquisition of each stream packet
significantly exceeds the communication costs incurred in doing so.
We assume rational clients ignore messages outside of the protocol.
We root this assumption in the existing game theory literature, which
considers extra-protocol messages to be outside the strategy
space. Excluding these messages is reasonable because convincing
clients to act on messages outside the protocol specified by the
broadcaster requires i) convincing clients to install the new
protocol in addition to BAR Gossip and ii) ensuring that
rational clients expect the protocol to provide current and future
updates in a BAR environment without support from the live event's
source. If this assumption is violated - e.g. alternative, cheaper,
better source of the update appears - then liveness guarantees may be
eroded. With this assumption, we can demonstrate that, absent other
avenues for receiving the desired updates, rational clients benefit
from running our protocol.
Altruistic clients follow the protocol as given regardless of
costs, similar to correct clients in the traditional fault-tolerance
literature. Byzantine clients behave arbitrarily or according
to some unspecified utility function.
Non-Byzantine clients maintain clocks synchronized within  seconds of each other and communicate over point-to-point,
synchronous, and unreliable links using both TCP and UDP. When
messages are exchanged using UDP, a node that does not receive an
expected message assumes that the link dropped it.
seconds of each other and communicate over point-to-point,
synchronous, and unreliable links using both TCP and UDP. When
messages are exchanged using UDP, a node that does not receive an
expected message assumes that the link dropped it.
We assume that clients subscribe to the live broadcast prior to its
start and that non-Byzantine clients remain in the system for the
duration of the broadcast. Future work is needed to extend the
protocol to accommodate dynamic membership. Given our protocol's
reliance on short-term incentives rather than long-term reputations,
we are optimistic that such extensions will be feasible.
We also assume that each participant is limited to one identity. To
mitigate the threat of Sybil attacks [10], it must be
hard for participants to collect multiple identities. There exist
sophisticated techniques to combat Sybil attacks [37,41].
In our prototype, we take the simple approach of
limiting each IP address to one identity.
We make the standard assumption that cryptographic primitives, like
digital signatures, symmetric key encryption, and one-way functions,
cannot be subverted. Our protocol also requires that each private key
generates unique signatures: for a given 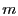 , there must exist exactly
one valid signature of , there must exist exactly
one valid signature of 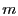 by by 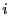 . Although a number of standard
signature algorithms fail to provide this property [29],
there exist algorithms that do [3]. We denote a
message . Although a number of standard
signature algorithms fail to provide this property [29],
there exist algorithms that do [3]. We denote a
message 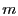 signed by signed by 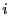 as as
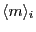 . .
We hold clients accountable for the messages they sign. We define a
proof of misbehavior (POM) to be a sequence of signed messages that
proves a client sent a message inconsistent with the protocol
specification. A POM against a client is sufficient evidence to evict that client from the population. Assuming that rational
clients gain benefit from being members of the population, we model
the system as an infinite game or one with an unpredictable end time
so that rational clients are cautious and do not risk eviction by
sending POMs.
Additional work is needed to determine if there are
significant end-game effects for known duration events.
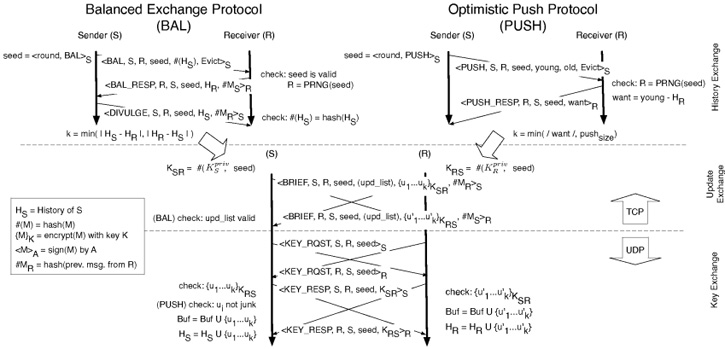 Figure 1:
Balanced Exchange and Optimistic Push Protocols for node
Figure 1:
Balanced Exchange and Optimistic Push Protocols for node
 contacting node contacting node  . During the update exchange, the upd_list
is sent in the Balanced Exchange protocol, but omitted for Optimistic Push. . During the update exchange, the upd_list
is sent in the Balanced Exchange protocol, but omitted for Optimistic Push.
The BAR Gossip protocol describes a method for an altruistic broadcaster to stream a live event to a pool of clients. Streaming
a live event requires that BAR Gossip guarantee two properties: i) non-Byzantine clients do not deliver unauthentic stream packets
(i.e., packets not generated by the broadcaster) and ii) every
altruistic client receives a large fraction of all stream packets in a
timely manner. As we later show, although we can provide the first
property in all situations, the second property is elusive, and we can
only provide it under good network conditions and with a limited
number of Byzantine clients.
Before the start time, each client generates a session key pair
consisting of a public and private key. Clients sign up for the event
by divulging both keys to the broadcaster. The broadcaster then
verifies the keys, closes the sign up service, and posts a list that
contains each client's identity, address, and public key. Clients
sign protocol messages using their private keys to provide
authentication, integrity, and non-repudiation of message contents.
During the live event, the broadcaster divides the stream into
discrete fixed-size chunks that we call updates. We structure
BAR Gossip as a sequence of rounds of duration  where updates are sent by the broadcaster and exchanged among clients. where updates are sent by the broadcaster and exchanged among clients.  is a time interval sufficient to complete the per-round message
exchanges required by our protocol. Round zero begins when the live
stream starts. Each update expires deadline rounds after it was
sent by the broadcaster. When an update expires, all clients that
possess that update deliver it to their media players. We consider an
update delivered by its deadline to be timely.
is a time interval sufficient to complete the per-round message
exchanges required by our protocol. Round zero begins when the live
stream starts. Each update expires deadline rounds after it was
sent by the broadcaster. When an update expires, all clients that
possess that update deliver it to their media players. We consider an
update delivered by its deadline to be timely.
In each round  , the broadcaster multicasts ups_per_round updates to
subsets of clients. Specifically, for each update, the broadcaster
selects nSeeds random clients to receive the update, signs the
update, and multicasts it to the selected clients. We require nSeeds to be large enough to guarantee that with high probability at
least one receiver is non-Byzantine. , the broadcaster multicasts ups_per_round updates to
subsets of clients. Specifically, for each update, the broadcaster
selects nSeeds random clients to receive the update, signs the
update, and multicasts it to the selected clients. We require nSeeds to be large enough to guarantee that with high probability at
least one receiver is non-Byzantine.
A client is unlikely to receive all updates directly from the
broadcaster and relies on two protocols to garner the remaining: Balanced Exchange and Optimistic Push. The Balanced Exchange Protocol allows clients to trade updates
one-for-one. That is, if client  has ten updates to offer client has ten updates to offer client
 and and  has only five to offer in return, then has only five to offer in return, then  and and  trade
five updates in each direction. Each balanced exchange is incentive-compatible [33]- rational clients
are motivated to follow its steps faithfully because no unilateral
deviation from the specified protocol can increase a client's expected
utility. trade
five updates in each direction. Each balanced exchange is incentive-compatible [33]- rational clients
are motivated to follow its steps faithfully because no unilateral
deviation from the specified protocol can increase a client's expected
utility.
Using the Balanced Exchange Protocol alone, however, is insufficient if a client
falls behind in obtaining updates (through bad luck or transient
network failures) because that client has little to offer in
exchanges. Once behind, a client may continue to fall farther behind.
The Optimistic Push Protocol provides a safety net. We call this protocol
optimistic because an initiator  is willing to forward useful
updates to is willing to forward useful
updates to  in the hope, rather than the certainty, that in the hope, rather than the certainty, that  will
return the favor. In this case, an unequal number of updates may be
exchanged- if will
return the favor. In this case, an unequal number of updates may be
exchanged- if  has fallen behind, has fallen behind,  helps helps  even if even if  cannot
fully reciprocate. cannot
fully reciprocate.
Although Optimistic Push is not an incentive-compatible protocol, we structure it
to encourage rational clients' participation, and our experimental
evidence suggests that a rational client will often benefit from
active participation in Optimistic Push. In the next sub-sections, we detail both
protocols, prove Balanced Exchange's incentive-compatibility and discuss rational
deviations within Optimistic Push. For reference,
Figure 1 illustrates both Balanced Exchange and Optimistic Push.
Balanced Exchange provides an incentive-compatible mechanism for rational clients
to exchange updates. In balanced exchanges, each party determines the
largest number of new updates it can exchange while keeping the trade
equal. A client concurrently executes two tasks: i) initiating
an exchange with another client and ii) responding to Balanced Exchange requests from other clients. As Figure 1
details, an exchange consists of four phases. In the first, partner selection, a client selects another client with whom to
trade. In the second, history exchange, the two parties learn
about the unexpired updates the other party holds and determines the
largest number  of updates that can be exchanged on a one-for-one
basis. In the third phase, update exchange, each party
deterministically generates an encryption key based upon its private
key and a per-exchange seed value. Each party then encrypts its of updates that can be exchanged on a one-for-one
basis. In the third phase, update exchange, each party
deterministically generates an encryption key based upon its private
key and a per-exchange seed value. Each party then encrypts its  most recent exchangeable updates and copies the encrypted updates into
a briefcase that is sent to the other party. In the fourth
phase, key exchange, the parties swap keys and decrypt the
contents of received briefcases. A client ends an exchange early in
the history exchange phase if that client realizes the exchange will
ultimately trade no updates. An exchange completes if both
clients execute all four phases or if one of them ends the exchange
early as allowed by the protocol. Clients communicate using TCP in the
first three phases, and switch to UDP in the fourth: we discuss the
reason for this choice in Section 4.2.4, where we
consider the incentives that motivate rational clients to exchange
keys.
most recent exchangeable updates and copies the encrypted updates into
a briefcase that is sent to the other party. In the fourth
phase, key exchange, the parties swap keys and decrypt the
contents of received briefcases. A client ends an exchange early in
the history exchange phase if that client realizes the exchange will
ultimately trade no updates. An exchange completes if both
clients execute all four phases or if one of them ends the exchange
early as allowed by the protocol. Clients communicate using TCP in the
first three phases, and switch to UDP in the fourth: we discuss the
reason for this choice in Section 4.2.4, where we
consider the incentives that motivate rational clients to exchange
keys.
Proofs of misbehavior (POMs) play an important role in BAR Gossip by
ensuring that clients who send internally inconsistent messages risk
eviction. Each message in our history and update exchanges includes a
cryptographic hash of the previous message sent in that balanced
exchange: if a client sends a briefcase whose contents differ from the
agreed upon updates of the history exchange, then the history exchange
messages plus the briefcase constitutes a POM.
We introduce a trusted agent of the broadcaster to audit possible
POMs. In every round, this auditor polices the system by
ordering a constant fraction of random clients to supply suspected
POMs against other clients. Note that the auditor can decrypt the
contents of well-formed briefcase messages because the broadcaster
supplies the auditor with every client's private key. If a queried
client does not have a POM against a peer, then the client must reply
with a dummy message. We specify all audit responses to be of equal
size, thereby removing a rational client's incentive to cover up POMs.
The auditor treats clients that ignore audit requests as it would
clients that have provably misbehaved. To reduce false positives
because of transient network failures, the auditor allows sufficient
time for a client to respond to audit requests. The auditor evicts a
misbehaving client by sending a signed eviction notice to the
broadcaster, who embeds all eviction notices in every update and stops
sending updates to evicted clients. We discuss in
Section 4.4 how to bound the overhead of eviction
notices.
Our approach to making Balanced Exchange robust to rational deviations follows two
principles: restricted choice and delayed gratification.
Restricted choice provides Balanced Exchange's safety property: if a rational client
decides to participate in an exchange, then that client sends only
messages as prescribed by the protocol. Delayed gratification
provides Balanced Exchange's liveness property: if links do not drop messages, then
two non-Byzantine clients participating in an exchange will complete
that exchange. We delay gratification by postponing a rational
client's receipt of useful updates until the last phase, key exchange.
In the next section, we prove these properties hold under a reasonable
set of assumptions.
We discuss Balanced Exchange's robustness against rational behavior within the
framework of Nash equilibria [28]. In a Nash
equilibrium, each client has a strategy and no client benefits from
changing its strategy while the other clients keep their strategies
unchanged. A limitation of Nash equilibria is that they do not
consider rational clients that collude to increase collective utility.
We empirically explore the impact of colluding rational clients in
Section 5.4, but future work is needed to design
gossip protocols with provable guarantees against such collusions.
In our analysis, we assume rational clients only consider strategies
that maximize the utility of each exchange independent of concurrent
or future exchanges. Our experiments demonstrate that this greedy
strategy performs well in a streaming environment where there is a
limited time to obtain useful updates. It is possible that more
sophisticated strategies optimizing over multiple exchanges are
superior to this myopic strategy; analyzing these strategies remains
future work. The Balanced Exchange Protocol guarantees the following property:
Theorem 1.
If two rational clients participating in a balanced exchange with
each other seek to maximize the utility of that exchange independent
of concurrent or future exchanges, then following the Balanced
Exchange Protocol is a Nash equilibrium.
In the following sections, we show that each phase of a balanced
exchange is a Nash equilibrium, implying that a balanced exchange is
also a Nash equilibrium.
In each phase, we show that if a rational client assumes it peers are
altruistic, then following Balanced Exchange is in that client's best interest.
Note that the assumption that remaining clients are altruistic is an
artifact of the Nash equilibria proof technique and is not a
requirement of our protocol.
We simplify the presentation of the subsequent lemmas and proofs by
treating any client that has issued a POM against itself as evicted.
We use the following property regarding eviction in later proofs and
include it here for reference.
Lemma 1.
A rational client  i) never issues a POM against itself and
ii) expects no benefit from communicating with evicted clients. i) never issues a POM against itself and
ii) expects no benefit from communicating with evicted clients.
Proof Sketch: i) Because rational clients are cautious by nature,  does not issue
a POM against itself for fear of being evicted. does not issue
a POM against itself for fear of being evicted.
ii) Suppose for contradiction that there exists an evicted
client  for whom for whom  expects positive benefit. Since expects positive benefit. Since  assumes
all other clients are following the protocol correctly and a client
can only be evicted by deviating from the protocol, assumes
all other clients are following the protocol correctly and a client
can only be evicted by deviating from the protocol,  must be an
altruistic client that deviates from the protocol, which is a contradiction. must be an
altruistic client that deviates from the protocol, which is a contradiction.
Problem: What if a rational client selects more
partners per round than prescribed or biases its selections instead of
choosing partners uniformly at random?
Partner selection highlights a fundamental difference between
traditional gossip and gossip in the BAR setting. In a traditional
gossip protocol, each client periodically selects a partner using a
pseudo-random number generator (PRNG) and contacts that partner to
request an exchange. Each client also accepts every request it
receives. Random partner selection provides robustness against
crashed clients, link failures, and targeted attacks. Yet, in a BAR
model, the freedom to choose partners allows rational clients to
select multiple partners not at random, thereby dissolving gossip's
guarantees. In BAR Gossip, a client generates an unpredictable,
deterministic seed for the PRNG to select a random partner, who can
then verify and accept the selection using the same PRNG or reject it
otherwise.
In BAR Gossip, a client  selects a partner for round selects a partner for round  by seeding
a PRNG with the signature by seeding
a PRNG with the signature
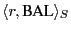 . .  then deterministically maps numbers generated by the PRNG to client
ids until it finds the first partner
then deterministically maps numbers generated by the PRNG to client
ids until it finds the first partner  for which it does not have an
eviction notice. This partner selection is deterministic, but
unpredictable because no client other than for which it does not have an
eviction notice. This partner selection is deterministic, but
unpredictable because no client other than  can generate can generate 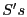 signature for a seed value. As Figure 1
illustrates, to initiate a gossip request to
signature for a seed value. As Figure 1
illustrates, to initiate a gossip request to  , ,  includes the
seed and all eviction notices for clients that includes the
seed and all eviction notices for clients that  could have selected
before could have selected
before  . .  then determines whether the seed is valid by
verifying that i) the seed is a valid signature, ii) then determines whether the seed is valid by
verifying that i) the seed is a valid signature, ii)  is the current round, iii) all included eviction notices are
valid, iv) the seeded PRNG generates
is the current round, iii) all included eviction notices are
valid, iv) the seeded PRNG generates  as the first
non-evicted client, and v) this is the first time that as the first
non-evicted client, and v) this is the first time that  has
presented this seed value to has
presented this seed value to  . If all five tests pass, then . If all five tests pass, then  accepts the gossip request from
accepts the gossip request from  ; otherwise, the seed is considered
invalid and ; otherwise, the seed is considered
invalid and  aborts the exchange. This selection algorithm
provides the following guarantee: aborts the exchange. This selection algorithm
provides the following guarantee:
Lemma 2.
Rational clients only send gossip requests to and accept gossip
requests from clients as prescribed by valid seeds.
Proof Sketch: A rational client  may communicate with (a) the uniquely defined
target sanctioned by the protocol, (b) an evicted node generated by
the PRNG before any non-evicted node, or (c) some other node. By
Lemma 1, (b) is not an option. Similarly, (c) is not an
option either because may communicate with (a) the uniquely defined
target sanctioned by the protocol, (b) an evicted node generated by
the PRNG before any non-evicted node, or (c) some other node. By
Lemma 1, (b) is not an option. Similarly, (c) is not an
option either because  will not be wrongly contacted by an
altruistic client nor would expect an altruistic client to engage in
an exchange not sanctioned by the protocol. This leaves option (a)
as the only feasible choice for a rational node. will not be wrongly contacted by an
altruistic client nor would expect an altruistic client to engage in
an exchange not sanctioned by the protocol. This leaves option (a)
as the only feasible choice for a rational node.
We note that the argument against clients participating in
unsanctioned exchanges is buttressed by the specific tangible concern
that such exchanges would be done without the recourse of sending a
POM to the auditor if either client in an exchange (quite rationally)
were to cheat its partner by sending a different briefcase than the
one agreed upon.
Problem: What if a rational client lies about having
(or not having) an update?
After a client  selects a partner selects a partner  , they exchange histories--a
history defines a set of update ids--using three messages. As
Figure 1 illustrates, , they exchange histories--a
history defines a set of update ids--using three messages. As
Figure 1 illustrates,  provides in the
first message a hash of its history provides in the
first message a hash of its history  and the PRNG seed value (as
discussed earlier) to and the PRNG seed value (as
discussed earlier) to  ; the hash is a verifiable promise to send a
given history. After verifying that ; the hash is a verifiable promise to send a
given history. After verifying that  is entitled to communicate
with is entitled to communicate
with  , ,  returns its current history returns its current history  . In the final message, . In the final message,
 divulges its actual history, divulges its actual history,  , to , to  who checks that the
previously sent hash is consistent with the divulged history. Note
that each client sends a history before learning its partner's
history: who checks that the
previously sent hash is consistent with the divulged history. Note
that each client sends a history before learning its partner's
history:  does so by sending a unique hash first and does so by sending a unique hash first and  by sending
its actual history while possessing only an irreversible hash. This
design promotes equal sharing, as neither client can tailor a history
to its partner's. In particular, this design makes it difficult for a
Byzantine client to maximize network traffic during the update
exchange by sending a history that is the exact complement of its
partner's. by sending
its actual history while possessing only an irreversible hash. This
design promotes equal sharing, as neither client can tailor a history
to its partner's. In particular, this design makes it difficult for a
Byzantine client to maximize network traffic during the update
exchange by sending a history that is the exact complement of its
partner's.
Lemma 3.
A rational client  does not divulge a history that does not match
the original hash. Similarly, does not divulge a history that does not match
the original hash. Similarly,  terminates any exchange in which
the divulged history does not match the original hash. terminates any exchange in which
the divulged history does not match the original hash.
Proof Sketch: If  were to sign messages indicating different histories for the
same exchange, then these messages constitute a POM and lead to
eviction. By Lemma 1, were to sign messages indicating different histories for the
same exchange, then these messages constitute a POM and lead to
eviction. By Lemma 1,  , being rational, would not do so. , being rational, would not do so.
Lemma 1 also ensures that  will not communicate with a client
that divulges a history not matching the original hash because such
actions would result in a POM. will not communicate with a client
that divulges a history not matching the original hash because such
actions would result in a POM.
Because update ids are public knowledge, a rational client  may
still consider reporting a history may
still consider reporting a history
 to increase
the expected utility in an exchange. Applying the principle of balanced cost [1], we define all histories to be of
fixed size, thereby removing any incentive to increase
the expected utility in an exchange. Applying the principle of balanced cost [1], we define all histories to be of
fixed size, thereby removing any incentive  may have to save a few
bytes by sending smaller histories. Therefore, the only way for may have to save a few
bytes by sending smaller histories. Therefore, the only way for  to obtain greater utility is by increasing the number of useful
updates
to obtain greater utility is by increasing the number of useful
updates  receives in each exchange. We show that rational clients
cannot increase expected utility by lying about histories. receives in each exchange. We show that rational clients
cannot increase expected utility by lying about histories.
Lemma 4.
Consider a rational client  and an unexpired update and an unexpired update
 .
If .
If  participates in an exchange, then participates in an exchange, then  reports a
history reports a
history
 such that such that
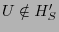 . .
Proof Sketch: Assume  deviates from the protocol by falsely claiming deviates from the protocol by falsely claiming
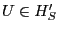 . .  does so if and only if it expects greater utility
without risking eviction. In order to obtain this greater utility
by falsely claiming does so if and only if it expects greater utility
without risking eviction. In order to obtain this greater utility
by falsely claiming
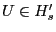 , ,  must send a briefcase
message that claims to contain must send a briefcase
message that claims to contain 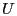 . Since . Since
 , such a
briefcase message is a POM. So according to Lemma 1, , such a
briefcase message is a POM. So according to Lemma 1,  does
not send it. does
not send it.
Lemma 5.
Consider a rational client  and an unexpired update and an unexpired update 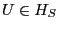 .
If .
If  participates in an exchange, then participates in an exchange, then  reports a
history reports a
history
 such that such that
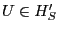 . .
Proof Sketch: Claiming
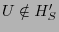 decreases the expected number of
useful updates to be exchanged. Since a rational client deviates if
and only if doing so increases expected utility, decreases the expected number of
useful updates to be exchanged. Since a rational client deviates if
and only if doing so increases expected utility,  would not claim would not claim
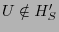 . .
Problem: What if a rational client places fake or
garbage data in briefcase messages?
After the history exchange commits  and and  to sending the to sending the  most
recent updates each possesses but the other lacks, most
recent updates each possesses but the other lacks,  and and  send
the corresponding updates contained in signed briefcases. Each
briefcase message contains i) the seed identifying this
exchange, ii) a plaintext description of send
the corresponding updates contained in signed briefcases. Each
briefcase message contains i) the seed identifying this
exchange, ii) a plaintext description of  update ids, and
iii) the corresponding update ids, and
iii) the corresponding  updates encrypted with the hash of
both the sender's private key and the exchange's seed value. The
sender signs the briefcase, promising that the encrypted contents
match the description. If either the received briefcase's seed value
does not match the seed identifying this exchange or the briefcase's
update list does not match the updates encrypted with the hash of
both the sender's private key and the exchange's seed value. The
sender signs the briefcase, promising that the encrypted contents
match the description. If either the received briefcase's seed value
does not match the seed identifying this exchange or the briefcase's
update list does not match the  expected updates, the receiver
aborts the exchange without sending its decryption key. expected updates, the receiver
aborts the exchange without sending its decryption key.
Lemma 6.
If a rational client  sends a briefcase message, then sends a briefcase message, then  includes the appropriate seed value and plaintext description for
that exchange.
includes the appropriate seed value and plaintext description for
that exchange.
Proof Sketch: By Lemma 1,  will not include an inappropriate
plaintext description, because the resulting briefcase message and
history exchange messages constitute a POM. will not include an inappropriate
plaintext description, because the resulting briefcase message and
history exchange messages constitute a POM.
 will also include the appropriate seed value and signature
because its partner will also include the appropriate seed value and signature
because its partner  is unwilling to accept a briefcase message
for which is unwilling to accept a briefcase message
for which  does not fear being audited. does not fear being audited.
 and and  exchange decryption keys in the next phase. If a client
receives a briefcase but not the corresponding decryption key, then
the client includes the briefcase as a suspected POM for a future
audit response. exchange decryption keys in the next phase. If a client
receives a briefcase but not the corresponding decryption key, then
the client includes the briefcase as a suspected POM for a future
audit response.
Lemma 7.
If a rational client  sends a briefcase message, then the encrypted
contents correspond to the briefcase's plaintext description. sends a briefcase message, then the encrypted
contents correspond to the briefcase's plaintext description.
Proof Sketch: A briefcase whose contents differ from the plaintext description is
a POM, which according to Lemma 1,  would never send. would never send.
Problem: What if a rational node chooses not to send
the key or sends an invalid key?
A client who is satisfied with its partner's briefcase enters the key
exchange phase. In this phase, the client sends via UDP a key request
containing the exchange seed and responds to key requests (also via
UDP) with a signed response that contains i) the seed value and
ii) the decryption key corresponding to the briefcase sent in
the previous phase.
The deterministic fair exchange of decryption keys is impossible to
solve without a trusted third party [32]. We
show that in the setting of BAR Gossip, altruistic and rational
clients can exchange keys fairly enough without a trusted third
party. The linchpin in providing this is to use a credible
threat. A client repeatedly sends key requests, up to some
constant number of times, until it obtains a key response from its
partner. Note that it is possible to tune the size of key requests to
offset any asymmetry between download and upload capacity.
Lemma 8.
If a rational client  responds to a key request, then responds to a key request, then 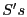 response contains the appropriate symmetric key.
response contains the appropriate symmetric key.
Proof Sketch: A key response whose contained key does not match the hash of the
seed and sender's private key is a POM, which by
Lemma 1,  does not send. does not send.
Lemma 9.
If a rational client  is satisfied with a client is satisfied with a client 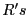 briefcase,
then briefcase,
then  responds to responds to 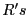 key requests. key requests.
Proof Sketch: Assume  ignores ignores 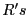 key requests. key requests.  deviates because it
expects greater utility from doing so. However, since deviates because it
expects greater utility from doing so. However, since  is
following the protocol, then is
following the protocol, then  quickly erodes quickly erodes 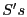 increase in
utility by making increase in
utility by making  receive multiple key requests. receive multiple key requests.
Lemma 10.
If a rational client  does not receive a key response from a
client does not receive a key response from a
client  , ,  will resend its key request. will resend its key request.
Proof Sketch: If  is following the protocol, is following the protocol,  reasons that the unreliability
of UDP is responsible for the delay. reasons that the unreliability
of UDP is responsible for the delay.  therefore resends the key
request because deviating by keeping silent decreases therefore resends the key
request because deviating by keeping silent decreases 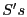 expected
utility. expected
utility.
The Optimistic Push Protocol provides a safety net for clients who
have fallen behind by allowing clients to obtain missing updates
without giving back a set of updates of equivalent value. Optimistic
pushes follow the same structure as balanced exchanges. Partner
selection is nearly identical. In round  , client , client  uses uses
 to seed the PRNG and ultimately selects a
partner to seed the PRNG and ultimately selects a
partner  in the same way as in the Balanced Exchange protocol. in the same way as in the Balanced Exchange protocol.
The main difference between Balanced Exchange and Optimistic Push lies
in what the parties disclose to each other during the history
exchange and in how they determine the content of their respective
briefcases during the update exchange. In particular, for the
history exchange  forwards to forwards to  two lists: a young list,
which contains the identifiers of some of the most recent updates two lists: a young list,
which contains the identifiers of some of the most recent updates  knows, and an old list, which contains the identifiers of
updates that
knows, and an old list, which contains the identifiers of
updates that  is missing and that are about to expire. If is missing and that are about to expire. If  has
nothing to offer from the old list, has
nothing to offer from the old list,  terminates the exchange.
Otherwise, terminates the exchange.
Otherwise,  replies with a want list, which contains the
identifiers of replies with a want list, which contains the
identifiers of  updates from the young list
that updates from the young list
that  is actually missing. is actually missing.  and and  then exchange briefcases. then exchange briefcases.
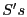 briefcase contains the briefcase contains the  updates from the want list with
an appropriate plaintext description of the update ids. updates from the want list with
an appropriate plaintext description of the update ids. 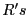 briefcase also contains
briefcase also contains  updates, but the plaintext description
does not identify the particular updates, only that updates, but the plaintext description
does not identify the particular updates, only that  items are
inside each of which can be either from the old list or junk, and at least one of those updates is from the old list. items are
inside each of which can be either from the old list or junk, and at least one of those updates is from the old list.
 places up to places up to  updates from updates from 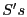 old list inside. If old list inside. If  has
has 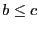 updates from updates from 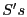 old list, then it includes those old list, then it includes those
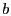 updates and updates and 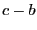 junk updates. It is this flexibility to
exchange deterministically generated junk data for good data that
allows a receiver that has fallen behind to catch up. junk updates. It is this flexibility to
exchange deterministically generated junk data for good data that
allows a receiver that has fallen behind to catch up.
We emphasize that junk updates are crafted to be larger than
real updates. If junk updates were smaller, the Optimistic Push
Protocol would encourage rational clients to deviate from the
Balanced Exchange Protocol because updates might be had for cheaper in
Optimistic Push. If junk updates were the same size as real updates,
a rational client may prefer to send junk to maintain the scarcity of
updates in that client's possession.
We regulate Optimistic Push with two parameters, push_age and
push_size: the young list consists only of updates that have
been broadcast within the last push_age rounds and push_size is an
upper limit on the number of updates that the Receiver can place in
its want list. Larger values of push_size help lagging clients
catch up faster; however, they also increase the likelihood that such
clients will waste bandwidth by sending junk.
The Optimistic Push Protocol follows nearly the same steps as the
Balanced Exchange Protocol. As a result, the above lemmas (except
Lemma 5) apply; a rational client may disingenuously
claim to not have an update to reduce the expected number of received
junk updates. Although restricted choice still limits the messages
that a rational client will send in the Optimistic Push Protocol, the
extra flexibility makes faithful participation less certain. For
example, rational clients may choose to deviate from the Optimistic
Push Protocol by simply not participating, never initiating pushes but
responding to them, or sending junk updates in lieu of useful updates.
Although we cannot prove that a rational client would faithfully
follow the Optimistic Push Protocol, our experimental evidence, in
Section 5, suggests that a rational client obtains
greater utility from following the protocol than from deviating.
Byzantine behavior is a reality of distributed systems. While
enticing rational clients to behave correctly in the presence of
Byzantine behavior, we must also limit the negative impact of such
behavior on good users of the system. In this paper we limit our
attention to Byzantine nodes that exploit the messages and behaviors
defined by our protocol.
In BAR Gossip, Byzantine nodes cannot subvert the system's safety
properties. Because the broadcaster signs each update, a Byzantine
node cannot tamper with the contents of any delivered update. With
respect to the liveness property stated in
Section 4.1, Byzantine nodes can impair
progress by sending two types of messages: non-protocol messages and
protocol messages. We regard generic DoS attacks based on non-protocol
messages (e.g. bandwidth or connection flooding) as outside the scope
of this protocol.
BAR Gossip is designed to be robust against protocol-based attacks on
liveness even if initiated by a significant number of Byzantine
clients. First, BAR Gossip's peer selection protocol limits the
number of nodes that one can contact in a round--unlike traditional
gossip, where a Byzantine node could potentially contact an unlimited
number of nodes and involve them in useless exchanges. Second,
Byzantine clients can inflict limited damage in the exchanges in which
they participate. A Byzantine client can remain silent during an
exchange to slow the spread of updates, but fortunately, gossip
protocols are naturally resilient to crash failures. One remaining
concern is that a Byzantine client could impact liveness by luring its
partners into expensive message exchanges that do not eventually
result in the dissemination of useful updates. We explore this kind
of attack in Section 5.5, where we show that altruistic clients still
deliver over 93% of updates in a timely manner even when 20% of the
clients are Byzantine.
To increase the practicality of BAR Gossip, we incorporate four
optimizations. First, to prevent a client from being overwhelmed by
valid gossip requests in a round, we use the standard heuristic that
each client accepts requests up to some per round maximum and ignores
further requests that round [4,8].
Second, to prevent spikes in used bandwidth, each client in a balanced
exchange limits the number of updates that are actually swapped,
similar to the Round Retransmission Limit optimization
of [4], by including this limit in history
exchanges. Third, the broadcaster embeds each eviction notice into a
constant number of updates, thereby bounding the overhead of each
eviction. With high probability, every client learns of an eviction
within deadline rounds.
Fourth, clients elide eviction notices that are older than deadline rounds
from gossip requests.
In this section, we show that BAR Gossip is a robust p2p streaming
protocol capable of providing stable and reliable throughput. We
evaluate BAR Gossip through experiments and simulations - we denote
figures derived from simulation data with "[sim]".
Our evaluation demonstrates that BAR Gossip:
- Outperforms traditional gossip in the presence of rational
clients
- Prevents unilateral rational deviation
- Is stable in the presence of significant collusion
- Tolerates up to
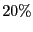 of the clients being Byzantine of the clients being Byzantine
Several parameters regulate the Balanced Exchange and Optimistic Push
Protocols. The broadcaster multicasts ups_per_round updates per round
and sends each update to nSeeds random clients. Each update
expires deadline rounds after it was multicast. In optimistic
pushes, push_age denotes the maximum age of updates sent in the young
list, while push_size is the maximum length of the want list. The
ratio of junk update size to real update size is junk_cost .
Table 1 provides the values for these parameters
for our simulation and prototype experiments. We use lower parameter
settings for the simulation, so that our simulator would terminate in
a reasonable amount of time. Note that we maintain approximately the
same ratio of push_size to ups_per_round in both settings. .
Table 1 provides the values for these parameters
for our simulation and prototype experiments. We use lower parameter
settings for the simulation, so that our simulator would terminate in
a reasonable amount of time. Note that we maintain approximately the
same ratio of push_size to ups_per_round in both settings.
| Protocol Parameter |
Simulation |
Prototype |
| ups_per_round(updates) |
10 |
98-101 |
| nSeeds(clients) |
25 |
3 |
| deadline(rounds) |
10 |
10 |
| push_size(updates) |
2 |
20 |
| push_age(updates) |
3 |
3 |
| junk_cost |
2 |
1.39 |
| # clients |
250 |
45 |
Table 1:
Parameter settings used in simulations and prototype experiments.
|
For our prototype evaluations, we implement BAR Gossip in Python to
stream an MPEG-4 video [34].
We recorded a 200 Kbps UDP video stream at 30 frames per second using
Quicktime Broadcaster with one key frame every 60 frames. Quicktime
Broadcaster generates UDP datagrams for the broadcast with an average
size of 179 bytes (
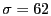 ), resulting in 116-131 datagrams per
second. ), resulting in 116-131 datagrams per
second.
Our broadcaster, auditor, and clients are a mix of 45 600 MHz and 850
MHz Emulab machines sharing a 100 Mbps Ethernet subnet, configured
with a 100ms end-to-end latency and 1% probability of any packet
being dropped. The broadcaster reads the recorded video from disk,
encapsulates on average three UDP datagrams into an update, pads every
update to the same size (640 bytes), and unicasts each update using
UDP to a random five clients. Clients then exchange updates as in
Figure 1. A client delivers an update by
extracting the contained datagrams and sending them to the local
Quicktime client that displays the video content. We use MD5 to
compute cryptographic hashes, RSA with full domain
hashing [3] to create unique signatures and the
Mersenne Twister algorithm [24] to generate
pseudo-random numbers.
Each client used on average 299 Kbps of upload bandwidth.
In the following sections we measure the reliability (expressed as the
percentage of updates received by the deadline), jitter (measured as
the percentage of rounds in which any update missed its deadline), and
bandwidth characteristics of BAR Gossip. Unless otherwise noted,
measurements in simulations are averaged over 1000 rounds and using
the prototype are averaged over 180 rounds across 15 trials. Error
bars are small in our data and elided from graphs for clarity.
We now compare BAR Gossip against a traditional push-pull gossip
protocol [8], where each client following the
protocol randomly selects one partner per round, exchanges histories,
and then exchanges missing updates. We demonstrate that this
traditional protocol is ill-suited for a BAR environment even when no
client is Byzantine and every rational client initiates only one
exchange per round. The intuition here is that a rational client
maximizes its utility by not sending updates. Altruistic clients,
therefore, do all the work of disseminating information in the system.
Figures 2 and 3 plot
the reliability seen and bandwidth used, respectively, by an
altruistic client as the proportion of rational clients in the system
increases. While BAR Gossip's lines remain relatively constant in
both graphs, traditional gossip's degrades noticeably.
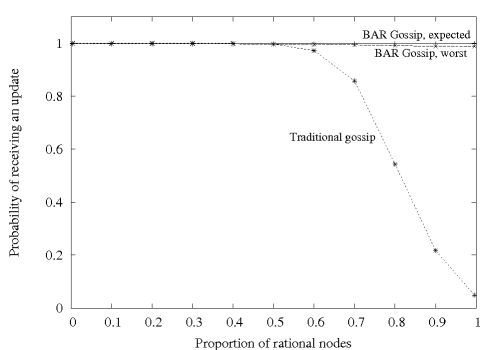 Figure 2:
[sim] Reliability experienced by an altruistic
client using traditional gossip versus BAR Gossip.
Figure 2:
[sim] Reliability experienced by an altruistic
client using traditional gossip versus BAR Gossip.
We include two lines for BAR Gossip because although we can prove a
rational client will faithfully participate in balanced exchanges, we
do not have a similar proof for optimistic pushes. The ``BAR Gossip,
expected'' line plots the best reliability an altruistic client can
see using BAR Gossip, corresponding to the case where rational clients
faithfully participate in optimistic pushes. We label the line
``expected'' because our empirical data suggests rational clients
obtain greatest utility by actually following the Optimistic Push Protocol. The
``BAR Gossip, worst'' line represents the case where rational clients
never initiate optimistic pushes and send as much junk in briefcases
as the protocol allows. Among the strategies we consider (see
Section 5.3), this second strategy yields the
worst reliability for an altruistic client.
Figure 2 shows that a client following BAR
Gossip receives almost all updates even when all other clients are
rational. In contrast, altruistic clients in traditional gossip
experience significantly lower reliability once the number of rational
clients exceeds 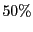 . When all clients but one are rational,
traditional gossip provides only the reliability that the broadcaster
can guarantee alone. . When all clients but one are rational,
traditional gossip provides only the reliability that the broadcaster
can guarantee alone.
 Figure 3:
[sim] Send bandwidth used by an altruistic client
using traditional gossip versus BAR Gossip.
Figure 3:
[sim] Send bandwidth used by an altruistic client
using traditional gossip versus BAR Gossip.
Figure 3 illustrates that in BAR Gossip an
altruistic client's consumed bandwidth is nearly independent of the
proportion of rational clients.
Traditional gossip, on the other hand, requires altruistic clients to
shoulder the entire burden of spreading updates, with bandwidth
spiking sharply when rational clients account for 70% of the system,
before tumbling down to almost nothing. This dramatic fall coincides
with the sharp decline in reliability in
Figure 2. In these areas of the graphs,
rational clients receive the majority of multicast updates and decline
to spread them, reducing both reliability and bandwidth devoted to
gossiped data.
We now examine deviant strategies that a rational client might pursue.
In our experiments, a rational client pursues these strategies while
the remaining clients continue to follow the protocol as specified.
Note that this is the experimental analog to the standard Nash
equilibrium proof technique.
In this analysis, we make two simplifying assumptions. First, a
rational client's primary concern is to improve the delivered stream's
quality by maximizing reliability and minimizing jitter; minimizing
consumed bandwidth is a subordinate goal. Second, a rational client
missing one or more updates always expects positive utility from
participating in a balanced exchange. Under this second assumption,
rational clients faithfully execute the Balanced Exchange Protocol. We now
consider the choices available to a rational client with respect to
Optimistic Push.
Table 2:
Six strategies a rational client may follow with regards to
the Optimistic Push Protocol.
| Strategy |
Accepts OP |
Initiates OP |
Returns |
| Proactive/Data |
Yes |
Yes |
Data |
| Proactive/Junk |
Yes |
Yes |
Junk |
| Proactive/Decline |
No |
Yes |
None |
| Passive/Data |
Yes |
No |
Data |
| Passive/Junk |
Yes |
No |
Junk |
| Passive/Decline |
No |
No |
None |
|
Table 3:
Rational client's experienced jitter pursuing
different strategies.
| Strategy |
Avg. Jitter |
Std. Deviation |
|
| Proactive/Data |
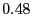 % % |
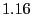 % % |
|
| Proactive/Junk |
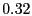 % % |
 % % |
|
| Proactive/Decline |
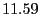 % % |
 % % |
|
| Passive/Data |
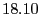 % % |
 % % |
|
| Passive/Junk |
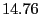 % % |
 % % |
|
| Passive/Decline |
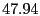 % % |
 % % |
|
|
Table 2 lists the five strategies we consider
that a rational client may pursue to deviate from the Optimistic Push Protocol.
Proactive strategies dictate that a rational client initiates
optimistic pushes as specified by the Optimistic Push Protocol. In contrast,
passive strategies specify to never initiate optimistic pushes.
Data, junk, and decline strategies prescribe that rational
clients responding to an optimistic push send useful updates (when
possible), send as much junk as allowed, or decline the exchange,
respectively. Note that following the Optimistic Push Protocol corresponds to
the the Proactive/Data strategy.
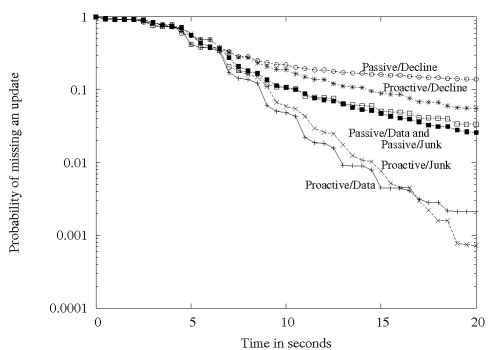 Figure 4:
Probability of a rational client missing an update
for different strategies.
Figure 4:
Probability of a rational client missing an update
for different strategies.
Figure 4 shows for each of the six
strategies the probability that the rational client will miss an
update, where lower lines correspond to better reliability.
Table 3 provides the
corresponding jitter for each strategy. When taken together,
Figure 4 and
Table 3 imply that rational
clients will follow either proactive/data or proactive/junk
strategies. This is perhaps not surprising, given that proactive
strategies perform additional exchanges that are likely to result in
more deliverable updates than passive strategies.
 Figure 5:
Rational client's consumed bandwidth for different strategies.
Figure 5:
Rational client's consumed bandwidth for different strategies.
The tie breaker between the top two strategies comes from
Figure 5, in which proactive/data uses
an average of 300 Kbps of upload bandwidth compared against
proactive/junk's 317 Kbps. This is not an accident: we have designed BAR Gossip with junk_cost so that rational clients
prefer filling their briefcases with valuable updates, rather than
junk, whenever possible. so that rational clients
prefer filling their briefcases with valuable updates, rather than
junk, whenever possible.
The conclusion we draw from this set of experiments is that a rational
client, when surrounded by other clients that follow BAR Gossip, has
no obvious incentive for deviation--in fact, quite the contrary.
While our experiments clearly fall short of proving that BAR Gossip as
a whole (Balanced Exchange plus Optimistic Push) constitutes a Nash
equilibrium, it does suggest that a Nash equilibrium is likely to be
found at or near the strategy that corresponds to BAR Gossip. For
instance, while we are unable to prove that there are no beneficial
hybrid strategies that, depending on the environment, switch between
two or more of the the six strategies we have considered, it appears
that the benefit of a proactive strategy derives from consistently
participating in more exchanges, making it unlikely that switching
occasionally to a passive strategy would provide a net gain. As for
switching among proactive strategies, it yields no change in benefit
while changing bandwidth costs, also providing little room for
improvement.
Overall, we believe that the expected and worst case lines in
Figures 2 and 3
provide a reasonable bound on the actual behavior of rational clients
in BAR Gossip, and that the likely behavior is near the expected line.
We now explore the effect of multiple rational clients coordinating
their actions to maximize their collective utility. We perform a
series of simulations to assess the impact such a group may have on
clients following the protocol. A complete analysis that defines
optimal collusion strategies is future work.
We assume that colluding and non-colluding rational clients share a
utility function. We also assume that colluding clients run a private
protocol to disseminate updates among themselves. This protocol may
be an alternative BAR protocol or it may be a non-BAR protocol
bolstered by a high level of trust among colluding clients. We
simulate a perfect collusion scenario in which every colluding
client immediately broadcasts new updates within the group at no cost.
This source of updates reduces the incentive to fully participate in
the BAR Gossip protocol. In particular, colluding clients only run
the Balanced Exchange protocol.
Figure 6 shows how the size of a perfect
collusion group affects the quality of the stream seen by a client
following BAR Gossip. The intuition for the degraded performance is
i) a non-colluding client trades little when participating in a
balanced exchange with a colluding client and ii) colluding
clients do not participate in optimistic pushes. In perfect collusion
groups, colluding clients get most of their updates for free from
other colluding clients, reducing their contributions to the rest of
the system.
We find that when the collusion group size reaches 50% of the
participants, altruistic clients see an average convergence of 93%
for an update, resulting in an unusable stream. Although near-perfect
collusion among small groups seems plausible, it is unclear that
collusion on a large scale is a significant threat. As the colluding
group grows, so do the challenges of coordinating and trusting
clients. Ironically, as a colluding group grows, it might require BAR
Gossip to distribute updates internally as trust begins to break down
among members.
 Figure 6:
[sim] Effect of collusion on an altruistic
client's reliability when colluding clients are following the
passive/decline strategy.
Figure 6:
[sim] Effect of collusion on an altruistic
client's reliability when colluding clients are following the
passive/decline strategy.
Rational players behave according to a well-known utility function and
represent most of the clients in a p2p system across multiple
administrative domains. A few clients, however, may possess unknown
utility functions or behave arbitrarily due to ill-will or
malfunction, possibly affecting rational
behavior [1]. Note that these
Byzantine clients may be disinterested in stream packets and may
prefer maximizing damage irrespective of consumed bandwidth, allowing
strategies like DoS attacks.
To assess BAR Gossip's robustness to Byzantine participation, we
explore one malicious goal that a Byzantine client could possess. We
assume that this goal is the inverse of any rational player's: to
increase the cost and decrease the benefit of all rational clients.
We consider Byzantine behavior within the limits of the BAR Gossip
protocol, which, as discussed in Section 4.3, limits
Byzantine clients to degrading performance only through their own
exchanges.
In the following experiments, a Byzantine client provides a history
during a balanced exchange that is the complement of its partner's to
induce the other client to exchange the maximum number of
updates. During an optimistic exchange, a Byzantine client always
announces a complete young list and empty old list if initiating, and
requests the entire young list if receiving. A Byzantine client never
enters the update or key exchange phases, so as not to generate a POM
and risk eviction, but still inducing its partner to devote
significant bandwidth to the exchange without receiving any benefit.
The presence of Byzantine clients can be viewed as an increase in the
overhead associated with the environment as the costs associated with
Byzantine clients depends upon the probability of entering an exchange
with a Byzantine client.
To show worst case behavior under this attack, non-Byzantine
clients in our experiments ignore previous unproductive exchanges. We
elide proactive/decline and passive/decline strategies in which
rational clients decline to participate in optimistic pushes.
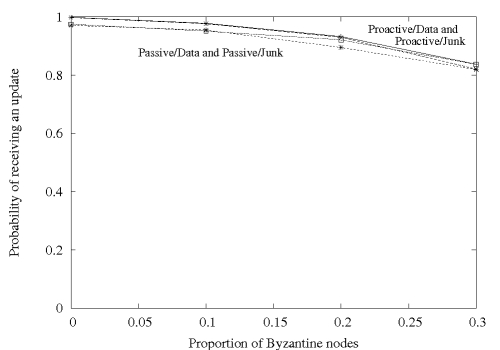 Figure 7:
Rational client's reliability for different strategies.
Figure 7:
Rational client's reliability for different strategies.
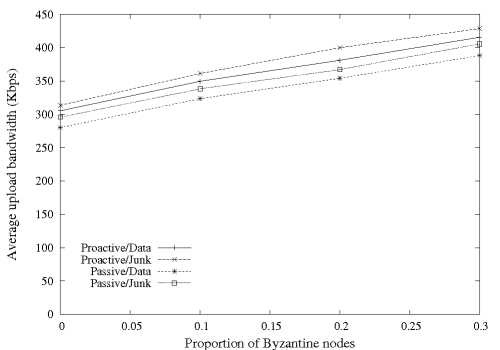 Figure 8:
Rational client's consumed bandwidth for different strategies.
Figure 8:
Rational client's consumed bandwidth for different strategies.
Figures 7 and 8 show the
reliability seen and bandwidth used, respectively, by a rational
client pursuing each strategy in the presence of different proportions
of Byzantine clients. The remaining non-Byzantine clients are
altruistic. The choice of strategies is similar to
Section 5.3 where we considered unilateral
deviation with no Byzantine clients. Passive and proactive strategies
deliver unwatchable video streams when the proportion of Byzantine
clients reaches 10% and 30%, respectively.
We conclude that among the strategies available, a rational client
should follow the protocol (proactive/data) regardless of the presence
of Byzantine clients. If all non-Byzantine clients are following the
protocol, with a system comprised of 20% Byzantine clients, the
bandwidth costs remain relatively constant while the convergence
suffers by less than 7%.
We present the first peer-to-peer data streaming application with
predictable throughput and low latency in the presence of correct,
selfish, and malicious nodes. At the core of our application is BAR
Gossip, the first gossip protocol defined under the BAR model. We
leverage a unique signature scheme to generate verifiable
pseudo-random numbers, allowing us to eliminate the opportunity for
rational nodes to hide behind nondeterminism without sacrificing the
benefits of the random communication pattern of gossip. Our
experiments and simulations show that our protocol provides good
convergence properties as long as no more than 20% of the nodes are
Byzantine or no more than 40% of the nodes collude. In both cases,
nodes following the protocol receive more than 93% of updates in a
timely manner.
The authors would like to thank the anonymous reviewers and Brad Chen
for shepherding our paper. We would also like to thank Jean-Phillipe
Martin, Vitaly Shmatikov and Peter Stone for helpful discussions about
game theory, signature schemes, and fair exchange.
This work was supported in part by NSF award CNS 0509338 and NSF
CyberTrust award 0430510.
- 1
-
A. S. Aiyer, L. Alvisi, A. Clement, M. Dahlin, J.-P. Martin, and C. Porth.
Bar fault tolerance for cooperative services.
In Proc. 20th SOSP, Oct. 2005.
- 2
-
G. Badishi, I. Keidar, and A. Sasson.
Exposing and eliminating vulnerabilities to denial of service attacks
in secure gossip-based multicast.
In DSN '04, page 223, Washington, DC, USA, 2004. IEEE
Computer Society.
- 3
-
M. Bellare and P. Rogaway.
Random oracles are practical: a paradigm for designing efficient
protocols.
In CCS '93, pages 62-73, New York, NY, USA, 1993. ACM Press.
- 4
-
K. P. Birman, M. Hayden, O. Oskasap, Z. Xiao, M. Budiu, and Y. Minsky.
Bimodal multicast.
ACM TOCS, 17(2):41-88, May 1999.
- 5
-
K. P. Birman, R. van Renesse, and W. Vogels.
Spinglass: Secure and scalable communications tools for
mission-critical computing.
In DARPA DISCEX-2001, 2001.
- 6
-
M. Castro, P. Druschel, A.-M. Kermarrec, A. Nandi, A. Rowstron, and A. Singh.
Splitstream: high-bandwidth multicast in cooperative environments.
In Proc. 19th SOSP, pages 298-313. ACM Press, 2003.
- 7
-
B. Cohen.
Incentives build robustness in bittorrent.
In Proc. 2nd IPTPS, 2003.
- 8
-
A. Demers, D. Greene, C. Houser, W. Irish, J. Larson, S. Shenker, H. Sturgis,
D. Swinehart, and D. Terry.
Epidemic algorithms for replicated database maintenance.
In Proc. of PODC '87, Aug. 1987.
- 9
-
A. K. Dixit and S. Skeath.
Games of Strategy.
W. W. Norton & Company, 1999.
- 10
-
J. R. Douceur.
The Sybil attack.
In Proc. 1st IPTPS, pages 251-260. Springer-Verlag, 2002.
- 11
-
P. Eugster, S. Handurukande, R. Guerraoui, A. Kermarrec, and P. Kouznetsov.
Lightweight probabilistic broadcast.
In Proc. of DSN '01, July 2001.
- 12
-
M. Feldman, C. Papadimitriou, J. Chuang, and I. Stoica.
Free-riding and whitewashing in peer-to-peer systems.
In Proc. PINS, pages 228-236. ACM Press, 2004.
- 13
-
A. J. Ganesh, A.-M. Kermarrec, and L. Massouliť.
Peer-to-peer membership management for gossip-based protocols.
IEEE Trans. Comput., 52(2):139-149, 2003.
- 14
-
I. Gupta, K. Birman, and R. van Renesse.
Fighting fire with fire: using randomized gossip to combat stochastic
scalability limits, 2002.
- 15
-
A. Habib and J. Chuang.
Incentive mechanism for peer-to-peer media streaming.
In 12th IEEE International Workshop on Quality of Service.,
2004.
- 16
-
S. D. Kamvar, M. T. Schlosser, and H. Garcia-Molina.
The eigentrust algorithm for reputation management in p2p networks.
In WWW '03, 2003.
- 17
-
S. Kremer, O. Markowitch, and J. Zhou.
An intensive survey of non-repudiation protocols.
Computer Communications, 25(17):1606-1621, Nov. 2002.
- 18
-
D. Levin, R. Sherwood, and B. Bhattacharjee.
Fair file swarming with fox.
In IPTPS, Feb 2006.
- 19
-
M.-J. Lin and K. Marzullo.
Directional gossip: Gossip in a wide area network.
In European Dependable Computing Conference, pages 364-379,
1999.
- 20
-
D. Malkhi, Y. Mansour, and M. K. Reiter.
Diffusion without false rumors: on propagating updates in a byzantine
environment.
Theor. Comput. Sci., 299(1-3):289-306, 2003.
- 21
-
D. Malkhi, E. Pavlov, and Y. Sella.
Optimal unconditional information diffusion.
In Proc. of DISC '01, pages 63-77, 2001.
- 22
-
D. Malkhi, M. Reiter, O. Rodeh, and Y. Sella.
Efficient update diffusion in byzantine environments.
In Proc. 20th SRDS, 2001.
- 23
-
S. Marti and H. Garcia-Molina.
Identity crisis: Anonymity vs. reputation in p2p systems.
In Proceedings of the 3rd International Conference on
Peer-to-Peer Computing, 2003.
- 24
-
M. Matsumoto and T. Nishimura.
Mersenne twister: a 623-dimensionally equidistributed uniform
pseudo-random number generator.
ACM Trans. Model. Comput. Simul., 8(1):3-30, 1998.
- 25
-
R. Melamed and I. Keidar.
Araneola: A scalable reliable multicast system for dynamic
environments.
In Proc. of NCA '04, pages 5-14, Washington, DC, USA, 2004.
- 26
-
Y. Minsky and F. Schneider.
Private communication.
- 27
-
A. Nandi, T.-W. J. Ngan, A. Singh, P. Druschel, and D. S. Wallach.
Scrivener: Providing incentives in cooperative content distribution
systems.
In Proceedings of the ACM/IFIP/USENIX 6th International
Middleware Conference (Middleware 2005), Grenoble, France, Nov. 2005.
- 28
-
J. Nash.
Non-cooperative games.
The Annals of Mathematics, 54:286-295, Sept 1951.
- 29
-
National Institute of Standards and Technology.
FIPS PUB 186-2: Digital Signature Standard (DSS).
Jan. 2000.
- 30
-
T.-W. Ngan, D. S. Wallach, and P. Druschel.
Incentives-compatible peer-to-peer multicast.
In 2nd Workshop on Economics of Peer-to-Peer Systems, 2004.
- 31
-
D. C. Oppen and Y. K. Dalal.
The clearinghouse: a decentralized agent for locating named objects
in a distributed environment.
ACM Trans. Inf. Syst., 1(3):230-253, 1983.
- 32
-
H. Pagnia and F. C. Gärtner.
On the impossibility of fair exchange without a trusted third party.
Technical Report TUD-BS-1999-02, Darmstadt University of Technology,
Department of Computer Science, Darmstadt, Germany, Mar. 1999.
- 33
-
D. C. Parkes.
Iterative Combinatorial Auctions: Achieving Economic and
Computational Efficiency.
PhD thesis, Department of Computer and Information Science,
University of Pennsylvania, May 2001.
- 34
-
A. Puri and A. Eleftheriadis.
Mpeg-4: an object-based multimedia coding standard supporting mobile
applications.
Mob. Netw. Appl., 3(1):5-32, 1998.
- 35
-
R. V. Renesse, Y. Minsky, and M. Hayden.
A gossip-style failure detection service.
Technical report, Ithaca, NY, USA, 1998.
- 36
-
P. Resnick, K. Kuwabara, R. Zeckhauser, and E. Friedman.
Reputation systems.
Commun. ACM, 43(12):45-48, 2000.
- 37
-
A. Rowstron and P. Druschel.
Storage management and caching in past, a large-scale, persistent
peer-to-peer storage utility.
In Proceedings of the 18th ACM Symposium on Operating Systems
Principles, pages 188-201. ACM Press, 2001.
- 38
-
R. van Renesse, K. P. Birman, D. Dumitriu, and W. Vogels.
Scalable management and data mining using astrolabe.
In Proc. of IPTPS '01, pages 280-294, London, UK, 2002.
Springer-Verlag.
- 39
-
R. van Renesse, H. Johansen, and A. Allavena.
Fireflies: Scalable support for intrusion-tolerant overlay networks.
In EuroSys '06, 2006.
- 40
-
W. Vogels, R. van Renesse, and K. Birman.
The power of epidemics: robust communication for large-scale
distributed systems.
SIGCOMM Comput. Commun. Rev., 33(1):131-135, 2003.
- 41
-
H. Yu, M. Kaminsky, P.B Gibbons, and A. Flaxman.
Sybilguard: Defending against sybil attacks via social networks.
In ACM SIGCOMM'06, Sept. 2006.
- 42
-
X. Zhang, J. Liu, B. Li, and T. P. Yum.
Donet/coolstreaming: A data-driven overlay network for live media
streaming.
In IEEE INFOCOM, Mar. 2005.
|
