| Alan Mislove†‡ | Ansley Post†‡ | Peter Druschel† | Krishna P. Gummadi† |
| †MPI-SWS | ‡Rice University |
Abstract:
Online communication media such as email, instant messaging, bulletin boards, voice-over-IP, and social networking sites allow any sender to reach potentially millions of users at near zero marginal cost. This property enables information to be exchanged freely: anyone with Internet access can publish content. Unfortunately, the same property opens the door to unwanted communication, marketing, and propaganda. Examples include email spam, Web search engine spam, inappropriately labeled content on YouTube, and unwanted contact invitations in Skype. Unwanted communication wastes one of the most valuable resources in the information age: human attention.
In this paper, we explore the use of trust relationships, such as social links, to thwart unwanted communication. Such relationships already exist in many application settings today. Our system, Ostra, bounds the total amount of unwanted communication a user can produce based on the number of trust relationships the user has, and relies on the fact that it is difficult for a user to create arbitrarily many trust relationships.
Ostra is applicable to both messaging systems such as email and content-sharing systems such as YouTube. It does not rely on automatic classification of content, does not require global user authentication, respects each recipient's idea of unwanted communication, and permits legitimate communication among parties who have not had prior contact. An evaluation based on data gathered from an online social networking site shows that Ostra effectively thwarts unwanted communication while not impeding legitimate communication.
1 Introduction
Internet-based communication systems such as email, instant messaging (IM), voice-over-IP (VoIP), online social networks, and content-sharing sites allow communication at near zero marginal cost to users. Any user with an inexpensive Internet connection has the potential to reach millions of users by uploading content to a sharing site or by posting messages to an email list. This property has democratized content publication: anyone can publish content, and anyone interested in the content can obtain it.
Unfortunately, the same property can be abused for the purpose of unsolicited marketing, propaganda, or disruption of legitimate communication. The problem manifests itself in different forms, such as spam messages in email; search engine spam in the Web; inappropriately labeled content on sharing sites such as YouTube; and unwanted invitations in IM, VoIP, and social networking systems.
Unwanted communication wastes human attention, which is one of the most valuable resources in the information age. The noise and annoyance created by unwanted communication reduces the effectiveness of online communication media. Moreover, most current efforts to automatically suppress unwanted communication occasionally discard relevant communication, reducing the reliability of the communication medium.
Existing approaches to thwarting unwanted communication fall into three broad categories. First, one can target the unwanted communication itself, by automatically identifying such communication based on its content. Second, one can target the originators of unwanted communication, by identifying them and holding them accountable. Third, one can impose an upfront cost on senders for each communication, which may be refunded when the receiver accepts the item as wanted. Each of these approaches has certain advantages and disadvantages, which we discuss in Section 2.
In this paper, we describe a method that exploits existing trust relationships among users to impose a cost on the senders of unwanted communication in a way that avoids the limitations of existing solutions. Our system, Ostra, (i) relies on existing trust networks to connect senders and receivers via chains of pairwise trust relationships; (ii) uses a pairwise, link-based credit scheme that imposes a cost on originators of unwanted communications without requiring sender authentication or global identities; and (iii) relies on feedback from receivers to classify unwanted communication. Ostra ensures that unwanted communication strains the originator's trust relationships, even if the sender has no direct relationship with the ultimate recipient of the communication. A user who continues to send unwanted communication risks isolation and the eventual inability to communicate.
The trust relationships (or social links) that Ostra uses exist in many applications. The links can be explicit, as in online social networking sites, or implicit, as in the links formed by a set of email, IM, or VoIP users who include each other in their contact lists. Ostra can use such existing social links as long as acquiring and maintaining a relationship requires some effort. For example, it takes some effort to be included in someone's IM contact list (making that person's acquaintance); and it may take more effort to maintain that status (occasionally producing wanted communication). With respect to Ostra, this property of a social network ensures that an attacker cannot acquire and maintain arbitrarily many relationships or replace lost relationships arbitrarily quickly.
Ostra is broadly applicable. Depending on how it is deployed, it can thwart unwanted email or instant messages; unwanted invitations in IM, VoIP, or online social networks; unwanted entries or comments in blogging systems; or inappropriate and mislabeled contributions to content-sharing sites such as Flickr and YouTube.
The rest of this paper is organized as follows. Section 2 describes existing approaches to preventing unwanted communication, as well as other related work. Section 3 describes a ``strawman" design that assumes strong user identities. Section 4 describes the design of Ostra and Section 5 discusses issues associated with deploying Ostra. Section 6 evaluates a prototype of Ostra on traces from an online social network and an email system. Section 7 sketches a fully decentralized design of Ostra. Finally, Section 8 concludes.
2 Related work
Unwanted communication has long been a problem in the form of email spam, and many strategies have been proposed to deal with it. However, the problem increasingly afflicts other communication media such as IM, VoIP, and social networking and content-sharing sites. In this section, we review existing approaches and describe how they relate to Ostra.
2.1 Content-based filtering
The most widespread approach to fighting unwanted communication is content-based filtering, in which recipients use heuristics and machine learning to classify communication automatically on the basis of its content. Popular examples include SpamAssassin [22] and DSPAM [7]. Content-based filters are also used for other types of unwanted communication, such as blog spam [17] and network-based security attacks [14].
Content-based filtering, however, is subject to both false positives and false negatives. False negatives -- that is, when unwanted communication is classified as wanted -- are a mere inconvenience. False positives [2] are a much more serious concern, because relevant messages are marked as unwanted and thus may not be received [13]. Moreover, there is a continual arms race [12] between spammers and filter developers, because the cognitive and visual capabilities of humans allow spammers to encode their message in a way that users can recognize but filtering programs have difficulty detecting.
2.2 Originator-based filtering
Another approach is to classify content by its originator's history and reputation. One such technique is whitelisting, in which each user specifies a list of other users from whom they are willing to receive content.
Whitelisting is commonly deployed in IM applications such as iChat and AIM, in VoIP systems such as Skype, and in social networking sites such as LinkedIn. In these cases, users have to be on each other's whitelists (i.e., their lists of contacts) to be able to exchange messages. To get on each other's whitelists, two users must exchange a special invitation. If the invitation is accepted, the two parties are added to each other's whitelists. If the invitation is rejected, then the inviter is added to the invitee's blacklist, which prevents the inviter from contacting the invitee again. RE [11] extends whitelists to automatically and securely include friends of friends.
To be effective, whitelisting requires that users have unique identifiers and that content can be authenticated; otherwise, it is easy for malicious users to make their communication seem to come from a whitelisted source. In most deployed email systems, messages cannot be reliably authenticated. However, secure email services, IM, VoIP services, and social networking sites can authenticate content. Whitelisting, however, cannot deal with unwanted invitations, another form of unwanted communication.
2.3 Imposing a cost on the sender
A third approach is to discourage unwanted communication by imposing a cost on the originators of either all communication or unwanted communication. The cost can be monetary or in terms of another limited resource.Quota- and payment-based approaches attempt to change the economics of unwanted communication by imposing a marginal cost on the transmission of an (unwanted) message.
Systems have been proposed in which senders must commit to paying a per-message fee or token before sending a digital communication [10,20,24]. These solutions attempt to model the postal service; they are based on the assumption that the cost will discourage mass distribution of unwanted messages. In some of the proposed systems, the per-message fee is charged only if the receiver classifies the messages as unwanted. This feature is important because originators of legitimate communication can still reach a large audience at low cost.
In general, deploying a decentralized email system that charges a per-message fee may require a micropayment infrastructure, which some have claimed is impractical [15,1,19]. Systems based on quotas do not need micropayments but still require a market for the distribution of tokens.
In challenge-response systems, the sender of a message must prove she is a human (as opposed to a computer program) before the message is delivered. Challenge-response systems can be viewed as imposing a cost on senders, where the cost is the human attention necessary to complete the challenge.
However, some automatically generated email messages (e.g., from an e-commerce site) are wanted; receiving such messages requires users to create a whitelisted email address to avoid false positives. Moreover, the need to complete a challenge may annoy and discourage some legitimate senders.
2.4 Content rating
Many content-sharing sites (e.g., YouTube [25]) use content rating. Users can indicate the level of interest, relevance, and appropriateness of a content item they have viewed. The content is then tagged with the aggregated user ratings. Content ratings can help users to identify relevant content and avoid unwanted content. These ratings can also help system administrators to identify potentially inappropriate content, which they can then inspect and possibly remove. Content rating is applicable only to one-to-many communication. Moreover, content-rating systems can be manipulated, particularly in a system with weak user identities.
2.5 Leveraging relationships
Online social relationships are used in Web-based applications for content sharing [25], socializing [9], and professional networking [16]. LinkedIn uses implicit whitelisting of a user's friends and offers a manual introduction service based on the social network. However, none of these sites leverages the social network to enable legitimate communication automatically among users who have not had prior contact, while thwarting unwanted communication.
Trust relationships are being used in the PGP web of trust [27] to eliminate the need for a trusted certificate authority. SybilGuard [26] uses social network links to identify users with many identities (Sybils). In Ostra, we use trust relationships to ensure that a user with multiple identities cannot send additional unwanted communication, unless she also has additional relationships.
3 Ostra strawman
In this section, we describe a strawman design of Ostra. The design is appropriate for trusted, centralized communication systems in which users have strong identities (i.e., each individual user has exactly one digital identity). We discuss the basic properties of this design in the context of two-party communication (e.g., email and IM), multi-party communication (e.g., bulletin boards and mailing lists), and content-sharing sites (e.g., YouTube and Flickr). Section 4 describes a refined design that removes the need for strong identities, because such identities are difficult to obtain in practice.
3.1 Assumptions
The strawman design is based on three assumptions.
- Each user of the communication system has exactly one unique digital identity.
- A trusted entity observes all user actions and associates them with the identity of the user performing the action.
- Users classify communication they receive as wanted (relevant) or unwanted (irrelevant).
Assumption 1 would require a user background check (e.g., a credit check) as part of the account creation process, to ensure that a user cannot easily create multiple identities; this assumption will be relaxed in Section 4. Assumption 2 holds whenever a service is hosted by a trusted Web site or controlled by a trusted tracker component; the trusted component requires users to log in and associates all actions with a user. We sketch a decentralized design that does not depend on this assumption in Section 7.
Producing communication can mean sending a email or chat message; adding an entry or comment to a blog; sending an invitation in an IM, VoIP, or social networking system; or contributing content in a content-sharing site. Receiving communication can mean receiving a message or viewing a blog entry, comment, or search result.
Typically, a user considers communication unwanted if she feels the content was not worth the attention. A user considers a blog entry, comment, or content object as unwanted if she considers the object to be inappropriate for the venue (e.g., site, group, or blog space) it was placed in or to have inappropriate search tags, causing the object to appear in response to an unrelated search.
3.2 System model
Figure 1 shows how Ostra interacts with a given communication system ![]() . Ostra is a separate module that runs
alongside the existing communication system. With Ostra, communication consists of three phases.
. Ostra is a separate module that runs
alongside the existing communication system. With Ostra, communication consists of three phases.
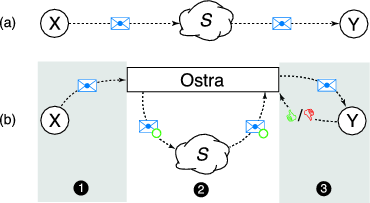 |
Authorization: When a sender wishes to produce a communication, she first passes the communication to Ostra. Ostra then issues a token specific to the sender, recipient, and communication. If the sender has previously sent too much unwanted communication, Ostra refuses to issue such a token and rejects the communication.
Transmission: Ostra attaches the token to the communication and transmits it using the existing communication mechanism. On the receiving side, Ostra accepts the communication if the token is valid. The communication is then provided to the recipient. Note that Ostra is not involved in the actual transmission of the communication.
Classification: The recipient classifies the communication as either wanted or unwanted, according to her personal preferences. This feedback is then provided to Ostra. Finally, Ostra makes this feedback available to the sender.
3.3 User credit
Ostra uses credits to determine whether a token can be
issued. Each user is assigned a credit balance, ![]() , with an
initial value of 0. Ostra also maintains a per-user balance
range
, with an
initial value of 0. Ostra also maintains a per-user balance
range ![]() , with
, with
![]() , which limits the range of the
user's credit balance (i.e.,
, which limits the range of the
user's credit balance (i.e.,
![]() at all times). We denote the balance and balance range for a
single user as
at all times). We denote the balance and balance range for a
single user as ![]() . For example, if a user's state is
. For example, if a user's state is
![]() , the user's current credit balance is 3, and it can
range between -5 and 6.
, the user's current credit balance is 3, and it can
range between -5 and 6.
When a token is issued, Ostra requires the sender to
reserve a credit and the receiver to reserve a place holder for this
credit in their respective credit balances. To make these
reservations,
the sender's ![]() is raised by one, and the receiver's
is raised by one, and the receiver's ![]() is lowered
by one. If these adjustments would cause either the sender's or the
receiver's credit balance to exceed the balance range, Ostra refuses
to issue the token; otherwise, the token is issued. When the
communication is classified by the receiver, the range adjustments are
undone. If the communication is marked as unwanted, one credit is transferred
from the sender to the receiver.
is lowered
by one. If these adjustments would cause either the sender's or the
receiver's credit balance to exceed the balance range, Ostra refuses
to issue the token; otherwise, the token is issued. When the
communication is classified by the receiver, the range adjustments are
undone. If the communication is marked as unwanted, one credit is transferred
from the sender to the receiver.
Let us consider an example in which both the sender's and the
receiver's initial balances are ![]() . When the token is issued,
the sender's balance changes to
. When the token is issued,
the sender's balance changes to ![]() , and the receiver's balance
changes to
, and the receiver's balance
changes to ![]() , representing the credit reservation.
Let us assume that the communication is classified as unwanted. In
this case, a credit is transferred from the sender to the receiver;
the receiver's balance becomes
, representing the credit reservation.
Let us assume that the communication is classified as unwanted. In
this case, a credit is transferred from the sender to the receiver;
the receiver's balance becomes ![]() , and the sender's becomes
, and the sender's becomes
![]() .
.
This algorithm has several desirable properties. It limits the amount of unwanted communication a sender can produce. At the same time, it allows an arbitrary amount of wanted communication. The algorithm limits the number of tokens a user can acquire before any of the associated communication is classified; thus, it limits the total amount of potentially unwanted communication a user can produce. Finally, the algorithm limits the number of tokens that can be issued for a specific recipient before that recipient classifies any of the associated communication; thus, an inactive or lazy user cannot cause senders to reserve a large number of credits, which would be bound until the communication were classified.
3.4 Credit adjustments
Several issues, however, remain with the algorithm described so far. When a user's credit balance reaches one of her credit bounds, she is, in effect, banned from producing (in the case of the lower bound) or receiving (in the case of the upper bound) any further communication. What can cause a legitimate user's credit balance to reach her bounds? Note that on the one hand, a user who receives unwanted communication earns credit. On the other hand, even a well-intentioned user may occasionally send communication to a recipient who considers it unwanted and therefore lose credit. Across all users, these effects balance out. However, unless a user, on average, receives precisely the same amount of unwanted communication as she generates, her credit balance will eventually reach one of her bounds. As a result, legitimate users can find themselves unable to communicate.
To address this problem, credit balances in Ostra decay towards 0 at a
constant rate ![]() with
with ![]() . For example, Ostra may be configured so that each
day, any outstanding credit (whether positive or negative) decays
by 10%. This decay allows an imbalance between the credit earned
and the credit lost by a user. The choice of
. For example, Ostra may be configured so that each
day, any outstanding credit (whether positive or negative) decays
by 10%. This decay allows an imbalance between the credit earned
and the credit lost by a user. The choice of ![]() must be high enough to cover the
expected imbalance but low enough to prevent considerable amounts of
intentional unwanted communication. As we show as part of Ostra's
evaluation, a small value of
must be high enough to cover the
expected imbalance but low enough to prevent considerable amounts of
intentional unwanted communication. As we show as part of Ostra's
evaluation, a small value of ![]() is sufficient to ensure that most
legitimate users never exceed their credit range.
is sufficient to ensure that most
legitimate users never exceed their credit range.
With this refinement, Ostra ensures that each user can produce
unwanted communication at a rate of at most
where
A denial of service attack is, however, still possible. Colluding
malicious users can inundate a victim with large amounts of unwanted
communication, causing the victim to acquire too much credit to
receive any additional communication. For these users, the rate of
decay may be too low to ensure that they do not exceed their credit
balances. To prevent such attacks, we introduce a special account, ![]() ,
that is not owned by any user and has no upper bound. Users with too
much credit can transfer credit into
,
that is not owned by any user and has no upper bound. Users with too
much credit can transfer credit into ![]() , thereby enabling
them to receive further communication. Note that the credit transferred
into
, thereby enabling
them to receive further communication. Note that the credit transferred
into ![]() is subject to the usual credit decay, so the total
amount of credit available to active user accounts does not diminish
over time. Additionally, users can only deposit credit into
is subject to the usual credit decay, so the total
amount of credit available to active user accounts does not diminish
over time. Additionally, users can only deposit credit into ![]() ; no withdrawals are allowed.
; no withdrawals are allowed.
Finally, there is an issue with communication failures (e.g., dropped
messages) and users who are offline for extended periods. Both may
cause the sender to reserve a credit indefinitely, because the
receiver does not classify the communication. The credit decay
does not help in this situation, because the decay affects only the credit
balance and not the credit bounds. Therefore, Ostra uses a
timeout ![]() , which is typically on the order of days. If a communication
has not been classified by the receiver after
, which is typically on the order of days. If a communication
has not been classified by the receiver after ![]() , the credit bounds are
automatically reset as though the destination had classified the
communication as wanted. This feature has the added benefit that it enables
receivers to plausibly deny receipt of communication. A receiver can
choose not to classify some communication, thus concealing its
receipt.
, the credit bounds are
automatically reset as though the destination had classified the
communication as wanted. This feature has the added benefit that it enables
receivers to plausibly deny receipt of communication. A receiver can
choose not to classify some communication, thus concealing its
receipt.
3.5 Properties
Ostra's system of credit balances observes the following invariant:
The conservation of credit follows from the fact that (i) users have an initial zero balance when joining the system, (ii) all operations transfer credit among users, and (iii) credit decay affects positive and negative credit at the same rate. Table 1 details how each operation leaves the overall credit balance unchanged. Thus, credit can be neither created nor destroyed. Malicious, colluding users can pass credits only between themselves; they cannot create additional credit or destroy credit. The amount of unwanted communication that such users can produce is the same as the sum of what they can produce individually.
We have already shown that each user can produce unwanted
communication at a rate of no more than ![]() . We now
characterize the amount of unwanted
subset of the user population can produce. Let us examine a group of
users
. We now
characterize the amount of unwanted
subset of the user population can produce. Let us examine a group of
users ![]() . Owing to the conservation of credit, users in this group
cannot conspire to create credit; they can only push credit between
themselves. Thus, the users in
. Owing to the conservation of credit, users in this group
cannot conspire to create credit; they can only push credit between
themselves. Thus, the users in ![]() can send unwanted communication to
users not in
can send unwanted communication to
users not in ![]() at a maximal rate of
at a maximal rate of
where
The implication of the above analysis is that we can characterize the total amount of
unwanted communication that non-malicious users can receive. Let us partition the
user population into two groups: group ![]() are ``good" users, who rarely send unwanted
communication, and group
are ``good" users, who rarely send unwanted
communication, and group ![]() are ``malicious" users, who frequently send unwanted communication.
Now, the maximal rate at which
are ``malicious" users, who frequently send unwanted communication.
Now, the maximal rate at which ![]() can receive unwanted communication from
can receive unwanted communication from ![]() is
is
which implies that, on average, each user in
However, we expect
Finally, Ostra has an incentive structure that discourages bad behavior and rewards good behavior. Table 2 shows a list of possible user actions and their costs and rewards.
3.6 Multi-party communication
Next, we show how the design can be used to support moderated multi-party communication, including mailing lists and content-sharing sites. The existing design generalizes naturally to small groups in which all members know each other. In this case, communication occurs as a series of pairwise events between the originator and each of the remaining group members.
In moderated groups, which are usually larger, a moderator decides on behalf of the list members if communication submitted to the group is appropriate. In this case, Ostra works exactly as in the two-party case, except that the moderator receives and classifies the communication on behalf of all members of the group.
Thus, only the moderator's attention is wasted by unwanted communication, and the cost of producing unwanted communication is the same as in the two-party case. However, an overloaded moderator may choose to increase the number of credits required to send to the group, to mitigate her load by discouraging inappropriate submissions.
Large content-sharing sites usually have content-rating systems or other methods for flagging content as inappropriate. Ostra could be applied, for instance, to thwart the submission of mislabeled videos in YouTube, by taking advantage of the existing ``flag as inappropriate" mechanism. When a user's video is flagged as inappropriate, it is reviewed by a YouTube employee; if it is found to be mislabeled, the submission is classified as unwanted for the purposes of Ostra.
Extending Ostra to work with unmoderated multi-party communication systems is the subject of ongoing work but is beyond the scope of this paper.
4 Ostra design
The strawman design described in the previous section requires strong user identities: that is, each individual user is guaranteed to have at most one unique digital identity. Such identities are not practical in many applications, as they require a background check as part of the account creation process. Such checks may not be accepted by users, and as far as we know, few services that require such a strong background check have been widely adopted on the Internet.
In this section, we refine the design of Ostra so that it does not require strong user identities. It is assumed that the communication system ensures that each identity is unique, but an individual user may sign up multiple times and use the system under different identities at different times. Our refined design leverages trust relationships to preserve Ostra's properties despite the lack of strong user identities. We still assume that a trusted entity such as a Web site hosts the communication service and runs Ostra. Later, in Section 7, we sketch out how Ostra could be applied to decentralized services.
The refined design of Ostra replaces the per-user credit balances with balances that are instead associated with the links among users in a trust network. We show that this mapping preserves the key properties of the strawman design, even though Ostra no longer depends on strong identities. We begin by defining a trust network and then describe how Ostra works with weak identities.
4.1 Trust networks
A trust network is a graph ![]() , where
, where ![]() is the set
of user identifiers and
is the set
of user identifiers and ![]() represents undirected links between user
identifiers who have a trust relationship. Examples of trust networks
are the user graph of an email system (where
represents undirected links between user
identifiers who have a trust relationship. Examples of trust networks
are the user graph of an email system (where ![]() is the set of
email addresses and
is the set of
email addresses and ![]() is the set of email contacts) and online
social networks (where
is the set of email contacts) and online
social networks (where ![]() is the set of accounts and
is the set of accounts and ![]() is the set
of friends). For convenience, we shall refer to two users connected
by an edge in the trust network as friends.
is the set
of friends). For convenience, we shall refer to two users connected
by an edge in the trust network as friends.
For the purposes of Ostra, a trust network must have the property that there is a non-trivial cost for initiating and maintaining links in the network. As a result, users in the trust network cannot acquire new relationships arbitrarily fast and cannot maintain an arbitrarily large number of relationships. We do not make any assumptions about the nature or the degree of trust associated with a relationship.
Finally, the trust network must be connected, meaning that there is a path of trust links between any two user identities in the network. Previous studies [18,4] have shown that the user graphs in existing social networks tend to be dominated by a single large component, implying that the networks are largely connected.
Ostra assumes that the users of a communication system are connected by a trust network and that Ostra has a complete view of this network.
4.2 Link credit
Because a user may have multiple identities, we can no longer associate a separate credit balance with each identity. Otherwise, a malicious user could gain additional credit and send arbitrary amounts of unwanted communication simply by creating more identities. Instead, Ostra leverages the cost of forming new links in trust networks to enforce a bound on each user.
Specifically, each link in the trust network is assigned a link
credit balance ![]() , with an initial value of 0, and a link
balance range
, with an initial value of 0, and a link
balance range ![]() , with
, with
![]() and
and
![]() .
These are analogous to the user credit balance and range in the
original design. We denote the balance and balance range
for a link
.
These are analogous to the user credit balance and range in the
original design. We denote the balance and balance range
for a link
![]() from
from ![]() 's perspective as
's perspective as
![]() . For example, if the link has
the state
. For example, if the link has
the state
![]() , then
, then ![]() is
currently owed 3 credits by
is
currently owed 3 credits by ![]() , and the balance can range between
-5 and 6.
, and the balance can range between
-5 and 6.
The link balance represents the credit state between the
user identities connected by the link. Ostra uses this balance to
decide whether to issue tokens. It is important to note that
the credit balance is symmetric. For example, if the link balance on
the
![]() link is
link is
![]() , then
, then ![]() is owed one credit by
is owed one credit by ![]() , or, from
, or, from ![]() 's
perspective,
's
perspective, ![]() owes
owes ![]() one credit (the latter can be denoted
one credit (the latter can be denoted
![]() ).
).
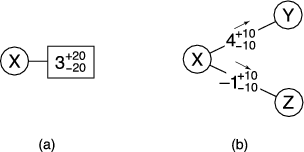
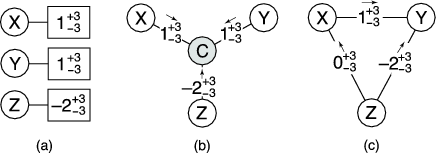
We map the user credit balance in the strawman design to a set of link credit balances on the user's adjacent links in the trust network. For example, as shown in Figure 2, if a user has two links in the trust network, the user's original credit balance is replaced with two separate credit balances, one on each link. However, we cannot compute a user balance by taking the sum of the link balances - in fact, the concept of a user balance is no longer useful because a user can create many identities and establish links between them. Instead, we introduce a new mechanism for credit transfer that uses link balances, rather than user balances, to bound the amount of unwanted communication that users can send.
We now describe this mechanism for transferring credits. For simplicity, we first describe the case of communication between users who are friends in the trust network. We then generalize the credit transfer mechanism to the case in which two arbitrary users wish to communicate.
4.2.1 Communication among friends
As in the strawman design, a user who wishes to send communication
needs to obtain a token during the authorization phase. For
example, a user ![]() may request to send communication to another user
may request to send communication to another user
![]() , a friend of
, a friend of ![]() 's. Ostra determines whether transferring this
credit would violate the link balance range on the
's. Ostra determines whether transferring this
credit would violate the link balance range on the
![]() link, and if not, it issues a signed token. The token is then
included in
link, and if not, it issues a signed token. The token is then
included in ![]() 's communication to user
's communication to user ![]() .
.
 |
As in the strawman design, Ostra allows users to have multiple
outstanding tokens by reserving credits for each potential transfer.
In the example in the previous paragraph, Ostra raises the lower bound for the
![]() link by one. This single adjustment has the effect
of raising
link by one. This single adjustment has the effect
of raising ![]() 's lower bound and lowering
's lower bound and lowering ![]() 's upper bound, because the
lower bound on the
's upper bound, because the
lower bound on the
![]() link can be viewed as the
upper bound on the
link can be viewed as the
upper bound on the
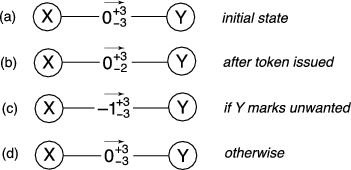
![]() link. Figure 3 shows the state of the
link. Figure 3 shows the state of the
![]() link during each stage of the transaction. By
adjusting the balance this way for outstanding tokens, Ostra ensures
that the link balance remains within its range regardless of how
the pending communication events are classified.
link during each stage of the transaction. By
adjusting the balance this way for outstanding tokens, Ostra ensures
that the link balance remains within its range regardless of how
the pending communication events are classified.
Later, in the classification stage, user ![]() provides Ostra with the
token and the decision whether
provides Ostra with the
token and the decision whether ![]() 's communication was wanted.
The balance range adjustment that was performed in the authorization
phase is then undone. Moreover, if
's communication was wanted.
The balance range adjustment that was performed in the authorization
phase is then undone. Moreover, if ![]() reports that the communication
was unwanted, Ostra adjusts the balance on the
reports that the communication
was unwanted, Ostra adjusts the balance on the
![]() link by subtracting one, thereby transferring a credit from
link by subtracting one, thereby transferring a credit from ![]() to
to
![]() . Thus, if the previous state of the link was
. Thus, if the previous state of the link was
![]() , the
final state would be
, the
final state would be
![]() , meaning
, meaning ![]() owes
owes ![]() one credit.
Finally, Ostra automatically cancels
the token after a specified timeout
one credit.
Finally, Ostra automatically cancels
the token after a specified timeout ![]() .
.
4.2.2 Communication among non-friends
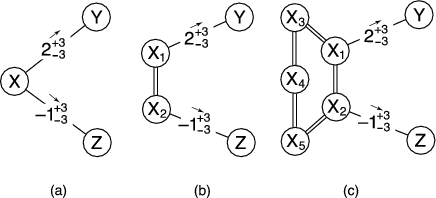
So far, we have considered the case of sending communication between two friends in the trust network. In this section, we describe how Ostra can be used for communication between any pair of users.
When a user ![]() wishes to send communication to a non-friend
wishes to send communication to a non-friend ![]() ,
Ostra finds a path consisting of trust links between
,
Ostra finds a path consisting of trust links between ![]() and
and ![]() . For example, such a path might be
. For example, such a path might be
![]() , where
, where ![]() and
and ![]() are friends in the trust
network, and
are friends in the trust
network, and ![]() and
and ![]() are also friends. When this path is found,
the range bounds are adjusted as before, but this occurs on every link in the
path. For example, if
are also friends. When this path is found,
the range bounds are adjusted as before, but this occurs on every link in the
path. For example, if ![]() wishes to send communication to
wishes to send communication to ![]() , Ostra
would raise the lower bound of both the
, Ostra
would raise the lower bound of both the
![]() and the
and the
![]() links by one.
Figure 4 shows a diagram of
this procedure.
If this adjustment can be done without violating any link ranges,
Ostra issues a token to
links by one.
Figure 4 shows a diagram of
this procedure.
If this adjustment can be done without violating any link ranges,
Ostra issues a token to ![]() .
.
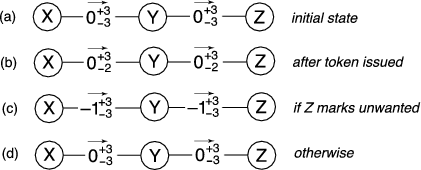 |
Similar to the transfer between friends, the token is then attached to ![]() 's
communication to
's
communication to ![]() . Later, in the classification stage,
. Later, in the classification stage, ![]() provides Ostra with the token and the decision whether the
communication was wanted. Now, the range adjustments on all the links
along the path are undone. If the communication was unwanted, the
credit is transferred along every link of the path;
Figure 4 (c) shows the result of this
transfer.
provides Ostra with the token and the decision whether the
communication was wanted. Now, the range adjustments on all the links
along the path are undone. If the communication was unwanted, the
credit is transferred along every link of the path;
Figure 4 (c) shows the result of this
transfer.
It is worth noting that the intermediate users along the path
are largely indifferent to the outcome of the transfer, as any credit
transfer will leave them with no net change. For example, consider
the scenarios shown in Figure 4 (c) and
(d). In either case, the total amount of credit that intermediate user ![]() has with all her friends is the same regardless of the outcome. If
has with all her friends is the same regardless of the outcome. If
![]() marks the communication as unwanted, as shown in Figure 4(c),
marks the communication as unwanted, as shown in Figure 4(c), ![]() owes a
credit to
owes a
credit to ![]() , but
, but ![]() now owes a credit to
now owes a credit to ![]() . Ostra allows users
to transfer credits along trust paths such that intermediate users
along the path are indifferent to the outcome.
. Ostra allows users
to transfer credits along trust paths such that intermediate users
along the path are indifferent to the outcome.
4.2.3 Generalization of Ostra strawman
One can show that Ostra generalizes the strawman design from the previous section.
Recall the account ![]() that is owned by the trusted site. Now, we
construct a trust network in which each user has a single link to
that is owned by the trusted site. Now, we
construct a trust network in which each user has a single link to ![]() ,
with the link balance and balance range equal to their user balance
and balance range in the strawman design. Ostra with such a trust
network has the same properties as the strawman design. To
see this, note that sending communication from
,
with the link balance and balance range equal to their user balance
and balance range in the strawman design. Ostra with such a trust
network has the same properties as the strawman design. To
see this, note that sending communication from ![]() to
to ![]() requires
raising the lower bound on the
requires
raising the lower bound on the
![]() link and lowering
the upper bound on the
link and lowering
the upper bound on the
![]() link, which is equivalent
to adjusting
link, which is equivalent
to adjusting ![]() 's and
's and ![]() 's user balance ranges in the same manner.
Figure 5 (b) shows an example of this
generalization for the specific set of user accounts in
Figure 5 (a).
's user balance ranges in the same manner.
Figure 5 (b) shows an example of this
generalization for the specific set of user accounts in
Figure 5 (a).
More importantly, Ostra preserves the conservation of credit that was present in the strawman system. This can be derived from the fact that credit is associated with links instead of users. Any credit in Ostra is naturally paired with a corresponding debt: for example, if the state of a link is
![]() , then
, then ![]() owes
owes ![]() one credit, but
one credit, but ![]() is owed a credit by
is owed a credit by ![]() . Thus, all outstanding credit is balanced by outstanding debt, implying that credit cannot be created or destroyed.
. Thus, all outstanding credit is balanced by outstanding debt, implying that credit cannot be created or destroyed.
The conservation of credit holds for each link independently, and is therefore independent of the trust network topology (Figure 5 (c) shows an example of a trust network with a different topology). As a result, the analysis of the strawman system in Section 3.5 applies to the full version of Ostra. For example, malicious, colluding users cannot conspire to manufacture credit; the amount of unwanted communication that such users can produce together is the sum of what they can produce independently.
 |
4.3 Security properties
We now discuss the security properties of Ostra's refined design in detail. Ostra's threat model assumes that malicious users have two goals: sending large amounts of unwanted communication, and preventing other users from being able to send communication successfully. Strategies for trying to send additional unwanted communication include signing up for multiple accounts and creating links between these accounts, as well as conspiring with other malicious users. Strategies for trying to prevent other users from communicating include targeting a specific user by sending large amounts of unwanted communication and attempting to exhaust credit on specific links in the trust network. In this section, we describe how Ostra handles these threats.
4.3.1 Multiple identities
One concern is whether users who create multiple identities (known as Sybils [6]) can send additional unwanted communication. Ostra naturally prevents such users from gaining additional credit.
To send unwanted communication to another user, a user must eventually
use one of her ``real" links to a different user, which has the same
effect as if the user only had a single identity. To see this, assume
a user with a set of multiple identities
![]() is sending to a different user
is sending to a different user ![]() . Now, regardless of how the links
between the identities in
. Now, regardless of how the links
between the identities in ![]() are allocated, any path between
are allocated, any path between ![]() and
and ![]() must contain a link
must contain a link
![]() , where
, where ![]() . If this property does not hold, then
. If this property does not hold, then ![]() , which is a
contradiction.
, which is a
contradiction.
 |
Thus, using per-link balances has the effect that the total credit available to a user no longer depends on the number of identities a user has. Instead, the credit available depends on the number of links the user has to other users. Figure 6 shows a diagram of how Ostra prevents users with multiple identities from sending additional unwanted communication.
Ostra allows users to create as many identities as they wish but ensures that they cannot send additional unwanted communication by doing so. Malicious users may attempt to use multiple Sybil identities to create multiple links to a single user. Although they may succeed occasionally, these links require effort to maintain and the malicious user, therefore, cannot create an unbounded number of them.
4.3.2 Targeting users
Another concern is whether malicious users could collectively send a large amount of unwanted communication to a user, thus providing this victim with too much credit to receive any additional messages. This attack is possible when the attacking users collectively have more links to legitimate users than the victim, as exhausting the credit on one of the victim's links requires the malicious users exhaust the credit on one of their own links.
However, the victim has a simple way out by forgiving some of the debt
on one of her links. If a user finds that she has too much credit on all of
her links, she can forgive a small amount of debt from one of her friends.
This is the same mechanism as transferring credit to the overflow account (![]() )
described in Section 3. To see this equivalence, consider
the star-topology trust network constructed in Section 4.2.3.
In that case, a user transferring credit to the overflow account is essentially forgiving
debt on their only link (to
)
described in Section 3. To see this equivalence, consider
the star-topology trust network constructed in Section 4.2.3.
In that case, a user transferring credit to the overflow account is essentially forgiving
debt on their only link (to ![]() ). This mechanism does
not allow malicious users to send additional unwanted communication to
the victim, as the victim only forgives debt to her direct friend (i.e., the victim's
friend does not repeat the process).
). This mechanism does
not allow malicious users to send additional unwanted communication to
the victim, as the victim only forgives debt to her direct friend (i.e., the victim's
friend does not repeat the process).
4.3.3 Targeting links
One final concern is whether malicious users could prevent large numbers of innocent users from communicating with each other by exhausting the credit on certain links in the trust network. If successful, such an attack could prevent a group of users from sending to the rest of the user population.
To exhaust the credit on specific links, attacking users would need both knowledge of the trust network topology and some control over trust path selection. Because the path selection is performed by the trusted site, the attacking users have the choice of only the destination and not the path. Even if we assume a powerful attacker who has control over the path selection, the trust network would need to have a topology that is susceptible to such an attack. For example, a barbell topology would be susceptible, as the link connecting the two halves of the network could be exhausted.
Analysis of current online social networks (which are typical trust networks) shows that these have a very dense core [18]. We show in Section 6 that the structure of these networks makes it unlikely that such an attack would succeed on a large scale.
5 Discussion
In this section, we discuss some issues associated with deploying Ostra.
5.1 Joining Ostra
Fundamentally, Ostra exploits the trust relationships in an existing social network of users to thwart unwanted communication. As a result, users are expected to acquire and maintain a certain number of social links to be able to communicate.
To join Ostra, a new user must be introduced to the system by an existing Ostra user. Requiring this form of introduction ensures that the trust network among users is connected and that each new user has at least one trust link. Thus, Ostra can be used only in conjunction with a ``invitation-only'' social network.
Users with few links in the trust network are more susceptible to credit exhaustion (whether accidental or malicious). Thus, there is an incentive for users to obtain and maintain a sufficient number of trust links. Establishing additional links can be done via the communication system after the user has joined Ostra. Link invitations are treated as normal messages, so users who attempt to send unwanted link invitations are blocked in the same manner as users who send other forms of unwanted communication.
5.2 Content classification
Ostra requires that recipients classify incoming communication as either wanted or unwanted. Providing explicit feedback is a slight burden on the user, but it may be a small price to pay for a system that responds to each user's preferences and is free of the misclassifications that are common in current content-based filtering systems [2]. Moreover, the feedback can often be derived implicitly from a user's actions; for instance, deleting a message probably indicates that the message was unwanted, whereas archiving or replying to the message strongly indicates that it was wanted.
As an optimization in message-based communication systems, a user could maintain a whitelist indicating users from whom communication is immediately and unconditionally classified as wanted. In this case, Ostra would need to operate only among users who are not on each other's whitelists.
5.3 Parameter settings
Ostra limits the amount of pending communication that a user can have,
where a pending item of communication is one that was generated by the
user but not yet classified by the receiver. In Section 6, we
show that Ostra's design parameters (![]() ,
, ![]() , and
, and ![]() ) can be
chosen such that most legitimate users are not affected
by the rate limit, while the amount of unwanted communication is still
kept very low.
) can be
chosen such that most legitimate users are not affected
by the rate limit, while the amount of unwanted communication is still
kept very low.
The ![]() parameter controls the number of unclassified
items of communication a user can have at any one time. A large
parameter controls the number of unclassified
items of communication a user can have at any one time. A large ![]() allows many outstanding messages but also admits the possibility that
a considerable amount of this outstanding communication would be
unwanted. In contrast, an
allows many outstanding messages but also admits the possibility that
a considerable amount of this outstanding communication would be
unwanted. In contrast, an ![]() close to 0 ensures that very little
unwanted communication is received, at the cost of potentially rate-limiting
legitimate senders. The
close to 0 ensures that very little
unwanted communication is received, at the cost of potentially rate-limiting
legitimate senders. The ![]() parameter represents the
rate at which users who have sent unwanted communication in the past
are ``forgiven".
Setting
parameter represents the
rate at which users who have sent unwanted communication in the past
are ``forgiven".
Setting ![]() too high allows additional unwanted communication, whereas
setting it too low may unduly punish senders who have inadvertently
sent unwanted communication in the past. In the Section 6,
we show that the conservative settings of
too high allows additional unwanted communication, whereas
setting it too low may unduly punish senders who have inadvertently
sent unwanted communication in the past. In the Section 6,
we show that the conservative settings of ![]() =-3 and
=-3 and ![]() =10% per day provide a
good trade-off in practice.
=10% per day provide a
good trade-off in practice.
5.4 Compromised user accounts
If a user's account password is compromised, the attacker can cause the user to run out of credit by sending unwanted communication. However, the amount of unwanted communication is still subject to the same limits that apply to any individual user. Moreover, a user would quickly detect that her account has been compromised, because she would find herself unable to generate communication.
6 Evaluation
In this section, we present an experimental evaluation of our Ostra prototype. Using data from a real online social network and an email trace from our institute, we show how Ostra can effectively block users from sending large amounts of unwanted communication.
6.1 Experimental trust network
To evaluate Ostra, we used a large, measured subset [18] of the social network found in the video-sharing Web site YouTube [25]. We extracted the largest strongly connected component consisting of symmetric links from the YouTube graph, which resulted in a network with 446,181 users and 1,728,938 symmetric links.
Strictly speaking, the YouTube social network does not meet Ostra's requirements, because there is no significant cost for creating and maintaining a link. Unfortunately, trust-based social networks that do meet Ostra's requirements cannot be easily obtained due to privacy restrictions. For instance, in the LinkedIn [16] professional networking site, users ``vouch" for each other; link formation requires the consent of both parties and users tend to refuse to accept invitations from people they do not know and trust. But, unlike YouTube, it is not possible to crawl the LinkedIn network.
However, we were able to obtain the degree distribution of users in the LinkedIn network. We found that both YouTube and LinkedIn degree distributions follow the power-law with similar coefficients. We used maximum-likelihood testing to calculate the coefficients of the YouTube and LinkedIn graphs, and found them to be 1.66 and 1.58 (the resultant Kolmogorov-Smirnov goodness-of-fit metrics were 0.12 and 0.05, suggesting a good fit). This result, along with the previously observed similarity in online social networks' structure [18], leads us to expect that the overall structure of the YouTube network is similar to trust-based social networks like LinkedIn.
Despite their structural similarity, the YouTube social network differs from the LinkedIn trust network in one important aspect: some users in YouTube collect many links (one user had a degree of over 20,000!). The maximum degree of users in actual trust-based social networks tends to be much smaller. Anthropological studies [8] have shown that the average number of relationships a human can actively maintain in the real world is about 150 to 200. Because the amount of unwanted communication a user can send in Ostra is proportional to her degree in the trust network, the results of our YouTube-based evaluation may understate the performance of Ostra on a real trust-based network.
6.2 Experimental traffic workload
We were unable to obtain a communication trace of the same scale as the social network we use. Therefore, we had to make some assumptions about the likely communication pattern within the social network. We expect that users communicate with nearby users much more often than they communicate with users who are far away in the social network. To validate this hypothesis, we collected an email trace from our organization, consisting of two academic research institutes with approximately 200 researchers. Our anonymized email trace contains all messages sent and received by the mail servers for 100 days, and the anonymized addresses in the trace are flagged as internal or external addresses.
Similar to previous studies [21,5], we extracted a social network from the email data by examining the messages sent between internal users. Specifically, we created a symmetric link between users who sent at least three emails to each other. We filtered out accounts that were not owned by actual users (e.g., helpdesk tickets and mailing lists), resulting in a large strongly connected component containing 150 users and covering 13,978 emails.
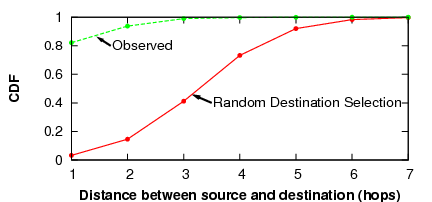 |
We then examined the social network distance between sender and receiver for all messages sent between these 150 users. Figure 7 compares the resulting distance distribution with one that would result had the senders selected random destinations. We found that the selection of senders had a very strong proximity bias: over 93% of all messages were sent to either a friend or a friend of a friend, compared to the expected 14% if the senders were chosen randomly. Thus, we expect that in practice, most communication in Ostra is directed to nearby users, significantly reducing the average path lengths in the trust network.
6.3 Setting parameters
We also used the email trace to determine the appropriate settings for
the Ostra parameters ![]() and
and ![]() . To do this, we examined the rate at
which users sent and received messages.
The trace contains 50,864 transmitted messages (an average of 3.39
messages sent per user per day) and 1,003,819 received messages (an
average of 66.9 messages received per user per day). The
system administrators estimated that the incoming
messages in the email trace consisted of approximately 95% junk
mail. Clearly, most of these receptions would not occur in an actual Ostra
deployment. However, we could not access the spam filter's per-message junk
mail tags, so we randomly removed 95% of the incoming messages
as junk.
. To do this, we examined the rate at
which users sent and received messages.
The trace contains 50,864 transmitted messages (an average of 3.39
messages sent per user per day) and 1,003,819 received messages (an
average of 66.9 messages received per user per day). The
system administrators estimated that the incoming
messages in the email trace consisted of approximately 95% junk
mail. Clearly, most of these receptions would not occur in an actual Ostra
deployment. However, we could not access the spam filter's per-message junk
mail tags, so we randomly removed 95% of the incoming messages
as junk.
To determine how often a given setting of ![]() and
and ![]() would affect
Ostra, we simulated how messages in the email trace would be delayed
due to the credit bounds.
We ran two experiments with different assumptions about the average delay between the
time when a message arrives and the time when the receiving user
classifies the message. We first simulated casual email users who classify messages
after six hours, and we then simulated heavy email users who classify messages after two hours.
would affect
Ostra, we simulated how messages in the email trace would be delayed
due to the credit bounds.
We ran two experiments with different assumptions about the average delay between the
time when a message arrives and the time when the receiving user
classifies the message. We first simulated casual email users who classify messages
after six hours, and we then simulated heavy email users who classify messages after two hours.
Table 3 presents the results of these two experiments with ![]() =-3 and
=-3 and ![]() =3.
We found that messages are rarely delayed (less than 1.5% of the
time in all cases), and that the average delay is on the order of a few hours.
We also found that the delays for receiving messages are
more significant than the delays for sending messages. We believe
this is an artifact of our methodology. Over 98%
of the delayed messages were received by just 3 users.
In practice, it is likely that these users (who receive a high volume of relevant email)
check and classify their email very frequently. This effect would reduce the frequency and
magnitude of delays, but our simulation does not account for it.
=3.
We found that messages are rarely delayed (less than 1.5% of the
time in all cases), and that the average delay is on the order of a few hours.
We also found that the delays for receiving messages are
more significant than the delays for sending messages. We believe
this is an artifact of our methodology. Over 98%
of the delayed messages were received by just 3 users.
In practice, it is likely that these users (who receive a high volume of relevant email)
check and classify their email very frequently. This effect would reduce the frequency and
magnitude of delays, but our simulation does not account for it.
6.4 Effectiveness of Ostra
In this section, we simulate deployments of Ostra in a message-based system (such as the messaging service on Flickr) and in a content-sharing system (such as YouTube). We evaluate Ostra under three traffic workloads: Random, where users select destinations randomly; Proximity, where users select destinations with the distribution that was observed in Section 6.2; and YouTube, where users send to a single YouTube account in the network. We show that in all cases, Ostra effectively bounds the rate at which malicious users can send unwanted communication while not impeding wanted communication.
6.4.1 Expected performance
Ostra limits the amount of unwanted communication that can be sent. A
single user user can send unwanted communication at a rate of at most
![]() , where
, where ![]() is the degree of the user. Thus, the rate at
which a malicious user can send unwanted communication is in direct
proportion to her degree. As the
is the degree of the user. Thus, the rate at
which a malicious user can send unwanted communication is in direct
proportion to her degree. As the ![]() or
or ![]() parameters are increased,
we expect the rate of unwanted communication to increase accordingly.
Additionally, as the proportion of malicious users in the network
increases, we expect the overall rate of unwanted messages to
increase.
parameters are increased,
we expect the rate of unwanted communication to increase accordingly.
Additionally, as the proportion of malicious users in the network
increases, we expect the overall rate of unwanted messages to
increase.
 |
6.4.2 Preventing unwanted communication
In this section we verify experimentally that Ostra performs as
described in Section 6.4.1. Unless otherwise noted, the
experiments were run with 512 randomly chosen attackers (approximately
0.1% of the population), ![]() =-3,
=-3, ![]() =3, and
=3, and ![]() =10% per day. Each
good user sent 2 messages and each attacker sent 500 messages.
=10% per day. Each
good user sent 2 messages and each attacker sent 500 messages.
To evaluate Ostra in the context of a content-sharing site, we modeled Ostra working in conjunction with YouTube. For these experiments, we configured the network so that uploading a video involves sending a message via Ostra to a single `YouTube' account in the network. An existing, well-connected user (1,376 links) in the core of the network was selected to represent this account.
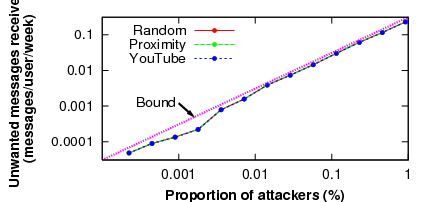
We first show that the rate at which users receive unwanted communication varies with the number of attacking users. In Figure 8, we present the results of experiments in which we vary the number of attackers in the network between 1 and 4,096 users (0.0002% to 1% of the network). We examine the rate at which unwanted messages were received by non-attacking users, along with the expected bound derived from the equations in Section 6.4.1.
As can be seen in Figure 8, Ostra effectively bounds the number of unwanted messages in proportion to the fraction of users who send unwanted communication. Even with 1% of the network sending unwanted messages, each legitimate user receives only 0.22 unwanted messages per week, translating to approximately 12 unwanted messages per year.
 |
Next, we explore Ostra's sensitivity to system parameter settings and
other conditions. Important parameters in Ostra are the credit bounds
![]() and
and ![]() for each link. If these bounds are set too high,
attackers can send many messages before being cut off. However, if
these bounds are set too low, a legitimate user could be
temporarily prevented from sending messages.
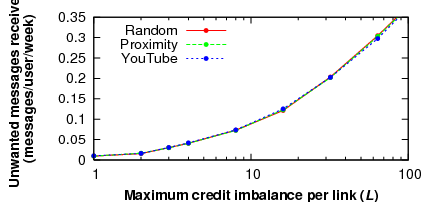
Figure 9 shows how the rate of
unwanted message delivery is affected by the maximal credit imbalance
across a link. As the maximum allowed imbalance increases, the amount
of unwanted communication received by good users increases, as
expected.
for each link. If these bounds are set too high,
attackers can send many messages before being cut off. However, if
these bounds are set too low, a legitimate user could be
temporarily prevented from sending messages.
Figure 9 shows how the rate of
unwanted message delivery is affected by the maximal credit imbalance
across a link. As the maximum allowed imbalance increases, the amount
of unwanted communication received by good users increases, as
expected.
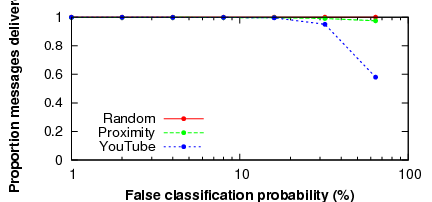 |
Finally, we examine the sensitivity of Ostra to the false positive rate of legitimate users' message classification. In other words, if users incorrectly mark other good users' messages as unwanted, how often are users blocked from sending message? We show how this probability of false classification affects the proportion of messages that cannot be sent in Figure 10. As can be seen, even a high false positive rate of 30% results in only a few blocked messages. This resiliency results from the rich connectivity of the social network (i.e., if one link becomes blocked, the users can route through other friends), and the fact that the false positive rate affects all users equally.
In the case of the content-sharing site, because all paths intersect, good users are blocked more quickly as the amount of content that is marked as unwanted increases. For example, when the false classification rate is 64%, about 40% of messages cannot be sent. However, it seems very unlikely that the moderator of a sharing site would misclassify content at such a high rate.
6.4.3 Resilience to link attacks
In a potential security attack discussed in Section 4, malicious users attempt to exhaust credit on a set of links inside the trust network, i.e., links other than the attackers' adjacent links. If successful, this attack could disrupt communication for innocent users. To evaluate whether a real-world social network is susceptible to this attack, we performed a min-cut analysis of the YouTube social network.
Assuming uniform link weights of one, we calculated the min-cuts between 3,000 randomly selected pairs of users. (A min-cut is a minimal set of links that, if removed, partitions two users; note that several such cuts can occur between two users.) We then looked for cases in which the set of links involved in a min-cut for a given pair of users differed from the set of links adjacent to either one of the two users. Such a min-cut could be the target of an attack, because the attackers could exhaust credit on this set of links before they exhaust the credit on their own links.
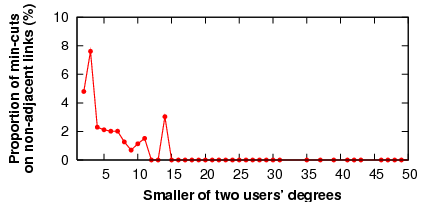 |
Figure 11 plots the proportion of user pairs for which the min-cut was not adjacent to one of the users, as a function of the lower of the two users' degrees. The results suggest that vulnerable links inside the network occur rarely, and that their frequency decreases with the degree of user connectivity. Therefore, the better connected users are in the trust network, the more robust the network is to link attacks. Because users in Ostra already have an incentive to maintain a certain number of links for other reasons, one would expect that a real Ostra trust network would not be vulnerable to link attacks.
7 Decentralizing Ostra
The design of Ostra we have described so far assumes the existence of a trusted, centralized component that maintains the trust network and credit state. This design is suitable for centralized communication systems, such as those hosted by a Web site. Peer-to-peer communication systems with a centralized ``tracker'' component can also use this design. However, completely decentralized systems like SMTP-based email cannot use it. In this section, we briefly sketch out a design of Ostra that works without any trusted, centralized components.
7.1 Overview
In the absence of a trusted, centralized entity, both the trust network and the credit state must be distributed. We assume that each participating user runs an Ostra software agent on her own computer. This Ostra agent stores the user's key material and maintains secure network connections to the Ostra agents of the user's trusted friends. The two Ostra agents adjacent to a trust link each store a copy of the link's balance and bounds.
Ostra authorization requires a route computation in the trust network. Because user trust networks can be very large (many online social networks have hundreds of millions of users), the path computation must be scalable. Moreover, it is assumed that users wish to keep their trust relationships private. In a centralized design, such privacy can be ensured easily. In the decentralized design, this concern complicates the distributed route computation, as no user has a global view of the trust network.
In the sections below, we sketch out distributed designs for the route computation, for maintaining link balances and for ensuring that users follow the Ostra protocol.
7.2 Routing
Routing in large networks is a well-studied problem. We use a combination of existing techniques for distributed route discovery in large trust networks.
We divide the problem into two cases. To find routes within the local neighborhood of a user (e.g., all users within three hops), we use an efficient bloom filter-based [3] mechanism. To discover longer paths, we use landmark routing [23] to route to the destination's neighborhood and then use bloom filters to reach the destination. Each user creates and publishes a bloom filter (representing her local neighborhood) and a landmark coordinate (representing her location in the global network).
A user's bloom filter represents the set of users within the two-hop neighborhood of the user's trust network. Thus, given a destination's bloom filter, a user can determine whether any of her friends are within the destination's two-hop neighborhood. If so, the user has found the next hop toward the destination. The solution works on arbitrary connected graphs. However, the approach is most efficient in sparse graphs in which the three-hop neighborhood accounts for a small percentage of the total network. Many real-world trust networks, such as social networks, have this property [18].
For long paths, we use landmark routing to reach the destination's neighborhood. A small subset of the user population is chosen as landmarks, and every user in the network determines her hop distance and the next hop to each of these landmarks. The landmarks are selected such that every user is within three hops of at least one landmark. Then, the resultant coordinate system can be used to route to within three hops of any destination user, and the bloom filters to reach the destination. Thus, given a destination user's coordinate, a user can first route to a landmark user who is ``near" the destination, and this landmark user can then use bloom filter routing for the last few hops.
Preliminary analysis reveals that these two mechanisms are practical. On the YouTube social network from Section 6, more than 90% of users' bloom filters are smaller than 4 kilobytes. Additionally, with only 765 users (0.16% of the population) as landmarks, the remaining users can route to more than 89% of the network. The remaining, unrouteable users are mostly weakly connected and possess only a single link. In a real Ostra trust network, such users would seek more trust relationships, making them reachable as well.
7.3 Decentralized credit update
When the path in the trust network between the sender and receiver has been determined, the credit balances and bounds are updated in a decentralized manner during authorization, classification, and token expiration.
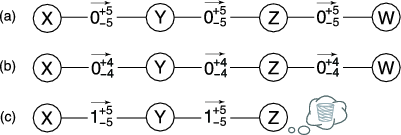
During authorization, the sender sends a signed authorization request message along the path. This request includes a unique identifier, the public key of the destination, and the destination's bloom filter and coordinate. Each user along the path (i) forwards the message, (ii) updates the balances and bounds of the message's incoming and outgoing links according to the rules stated below, (iii) records the destination, request identifier, previous hop, next hop, and expiration time of the request, and (iv) sets a timer for the expiration time. When the destination receives the request, it issues a signed token and sends it directly to the sender.
The link bounds are updated as follows. Each user along the path
increments the lower bound ![]() for the next hop, as was done in the
centralized Ostra described in Section 4. Thus, the
state of the network after a token is issued is exactly as shown in
Figure 4 (b).
for the next hop, as was done in the
centralized Ostra described in Section 4. Thus, the
state of the network after a token is issued is exactly as shown in
Figure 4 (b).
During classification, the destination sends a signed classification message along the path in the reverse direction. Each user checks if she has a record of a matching authorization request. If so, the adjustments of the link bounds performed during the authorization are undone, and the link balances are adjusted as described below. The message is then forwarded, and the record is deleted. Otherwise, if no matching record exists, the message is ignored.
The link balances are adjusted as was done in the centralized case. If the message was classified as wanted, the link balances are not changed, as shown in Figure 4 (d). However, if the message was classified as unwanted, each user raises the credit balance of the next hop in the path (the user to whom the original request was forwarded) and lowers the credit balance of the previous hop (the user from whom the original request was received). In this case, the resultant state of the network is shown in Figure 4 (c).
When the timer associated with an authorization request expires, then the user undoes the adjustments made to the link states during the authorization phase and deletes the request record.
Because authorization and classification messages are forwarded by the Ostra agents of users in the trust network, one concern is whether malicious users can simply drop such incoming messages. To protected against this, we provide users with an incentive to forward authorization requests and responses: users penalize the next hop along the path by lowering the next hop's credit if the message does not reach its destination.
 |
Each user along the path adjusts the next hop's upper bound ![]() by a
penalty amount during the authorization phase. When the message is
classified by the destination, the bound is restored. Otherwise, if a
user drops the message, each of the users
penalizes the next hop after the timeout
by a
penalty amount during the authorization phase. When the message is
classified by the destination, the bound is restored. Otherwise, if a
user drops the message, each of the users
penalizes the next hop after the timeout ![]() . An example is shown in
Figure 12: while the message is pending classification
(b), both the upper bound
. An example is shown in
Figure 12: while the message is pending classification
(b), both the upper bound ![]() and the lower bound
and the lower bound ![]() are changed
to account for all possible outcomes. In the case in which
are changed
to account for all possible outcomes. In the case in which ![]() drops the
message (c),
drops the
message (c), ![]() penalizes
penalizes ![]() , and
, and ![]() penalizes
penalizes ![]() .
Thus,
.
Thus, ![]() is penalized for dropping the message, whereas
is penalized for dropping the message, whereas ![]() , who
properly forwarded the message, has a neutral outcome.
, who
properly forwarded the message, has a neutral outcome.
8 Conclusion
We have described and evaluated Ostra, a system that leverages existing trust relationships among users to thwart unwanted communication. Unlike existing solutions, Ostra does not rely on strong user identities, does not depend on automatic content classification, and allows legitimate communication among users who have not had prior contact. Ostra can be applied readily to messaging and content-sharing systems that already maintain a social network. We have presented and evaluated a design of Ostra that works for systems with a trusted component (such as a Web site or a peer-to-peer system with a tracker). We have also sketched a design of Ostra which works with completely decentralized systems such as SMTP-based email. An evaluation based on data gathered from an online social networking site and an email trace shows that Ostra can effectively thwart unwanted communication while not impeding legitimate communication.
Acknowledgments
This work was supported in part by National Science Foundation grants ANI-0225660 and CNS-0509297. We would like to thank the anonymous reviewers and our shepherd Mike Dahlin for helpful comments, which greatly improved this paper. We would also like to thank Patrick Cernko for his assistance with the email trace used in the evaluation.
Bibliography
-
- 1
-
M. Abadi, A. Birrell, M. Burrows, F. Dabek, and T. Wobber.
Bankable postage for network services.
In Proceedings of the Asian Computing Science Conference (ASIAN'03), Mumbai, India, December 2003. - 2
-
S. Agarwal, V. N. Padmanabhan, and D. A. Joseph.
Addressing email loss with SureMail: Measurement, design, and evaluation.
In Proceedings of the 2007 Usenix Annual Technical Conference (USENIX'07), Santa Clara, CA, June 2007. - 3
-
B. H. Bloom.
Space/time trade-offs in hash coding with allowable errors.
Communications of the ACM, 13(7):422-426, 1970. - 4
-
M. Cha, H. Kwak, P. Rodriguez, Y.-Y. Ahn, and S. Moon.
I Tube, You Tube, Everybody Tubes: Analyzing the World's Largest User Generated Content Video System.
In Proceedings of the 5th ACM/USENIX Internet Measurement Conference (IMC'07), San Diego, CA, October 2007. - 5
-
A. Chapanond, M. S. Krishnamoorthy, and B. Yener.
Graph Theoretic and Spectral Analysis of Enron Email Data.
Computational & Mathematical Organization Theory, 11(3), October 2005. - 6
-
J. Douceur.
The Sybil Attack.
In Proceedings of the 1st International Workshop on Peer-To-Peer Systems (IPTPS'02), Cambridge, MA, March 2002. - 7
-
DSPAM.
https://dspam.nuclearelephant.com. - 8
-
R. Dunbar.
Coevolution of neocortical size, group size and language in humans.
Behavioral and Brain Sciences, 16(4):681-735, 1993. - 9
-
Facebook.
https://www.facebook.com. - 10
-
S. E. Fahlman.
Selling interrupt rights: A way to control unwanted e-mail and telephone calls.
IBM Systems Journal, 41(4):759-766, 2002. - 11
-
S. Garriss, M. Kaminsky, M. J. Freedman, B. Karp, D. Mazières, and H. Yu.
RE: Reliable Email.
In Proceedings of the 3rd Symposium on Networked Systems Design and Implementation (NSDI'06), San Jose, CA, May 2006. - 12
-
S. Hansell.
Internet Is Losing Ground in Battle Against Spam.
The New York Times, April 22, 2003. - 13
-
L. G. Harbaugh.
Spam-proof your in-box.
PCWorld, May 2004. - 14
-
S. Kumar, S. Dharmapurikar, F. Yu, P. Crowley, and J. Turner.
Algorithms to accelerate multiple regular expressions matching for deep packet inspection.
In Proceedings of the Annual Conference of the ACM Special Interest Group on Data Communication (SIGCOMM'06), Pisa, Italy, August 2006. - 15
-
J. R. Levine.
An overview of e-postage.
2003.
https://www.taugh.com/epostage.pdf. - 16
-
LinkedIn.
https://www.linkedin.com. - 17
-
G. Mishne and D. Carmel.
Blocking Blog Spam with Language Model Disagreement.
In Proceedings of the 1st International Workshop on Adversarial Information Retrieval on the Web (AIRWeb), Chiba, Japan, May 2005. - 18
-
A. Mislove, M. Marcon, K. P. Gummadi, P. Druschel, and B. Bhattacharjee.
Measurement and Analysis of Online Social Networks.
In Proceedings of the 5th ACM/USENIX Internet Measurement Conference (IMC'07), San Diego, CA, October 2007. - 19
-
A. M. Odlyzko.
The case against micropayments.
In Proceedings of Financial Cryptography: 7th International Conference, Gosier, Guadeloupe, January 2003. - 20
-
F.-R. Rideau.
Stamps vs spam: Postage as a method to eliminate unsolicited commercial email.
2002.
https://fare.tunes.org/articles/stamps_vs_spam.html. - 21
-
J. Shetty and J. Adibi.
The Enron Email Dataset Database Schema and Brief Statistical Report.
Technical report, University of Southern California Information Sciences Institute, 2004. - 22
-
SpamAssassin.
https://spamassassin.apache.org. - 23
-
P. F. Tsuchiya.
The Landmark Hierarchy: A New Hierarchy for Routing in Very Large Networks.
In Proceedings of the Annual Conference of the ACM Special Interest Group on Data Communication (SIGCOMM'88), Stanford, CA, August 1988. - 24
-
M. Walfish, J. Zamfirescu, H. Balakrishnan, D. Karger, and S. Shenker.
Distributed Quota Enforcement for Spam Control.
In Proceedings of the 3rd Symposium on Networked Systems Design and Implementation (NSDI'06), San Jose, CA, May 2006. - 25
-
YouTube.
https://www.youtube.com. - 26
-
H. Yu, M. Kaminsky, P. B. Gibbons, and A. Flaxman.
SybilGuard: Defending against Sybil attacks via social networks.
In Proceedings of the Annual Conference of the ACM Special Interest Group on Data Communication (SIGCOMM'06), Pisa, Italy, August 2006. - 27
-
P. R. Zimmermann.
The Official PGP User's Guide.
MIT Press, Cambridge, MA, USA, 1994.
About this document ...
Ostra: Leveraging trust to thwart unwanted communicationThis document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.